Сравнение квантовой и классической имитации отжига

Автор(ы):

• Бурдейный Дмитрий

Описание лекции

В этой лекции рассмотрим каноническую работу Quantum annealing in the transverse Ising model, опубликованную в 1998 году [KN98]. В ней двумя способами численно решается задача о нахождении основного состояния системы взаимодействующих спинов. Первый способ – обычная классическая имитация отжига, второй – имитация квантового отжига. Результаты применения этих подходов анализируются и сравниваются между собой.

Постановка задачи

Итак, рассматривается одномерная система взаимодействующих спинов, которая описывается гамильтонианом Изинга (полностью аналогичным тому, который был представлен в базовой лекции о модели Изинга):

$${\hat{H}}_0=-\sum _{i,j}{J}_{ij}{\hat{\sigma }}_i^z{\hat{\sigma }}_j^z-h\sum _i{\hat{\sigma }}_i^z,$$

где $J_{ij}$ – величины обменного взаимодействия для пар спинов, $h$ – внешнее поле (оно направлено вдоль оси $z$ и потому называется продольным – longitudinal). Требуется найти основное состояние гамильтониана ${\hat{H}}_0$, т.е. его собственное состояние, соответствующее его минимальному собственному значению.

Далее разберем численное решение этой задачи с помощью обычной классической имитации отжига (simulated annealing, SA для краткости) и с помощью квантовой имитации отжига (quantum annealing – QA).

Имитация квантового отжига (QA)

Как в предыдущей лекции об аннилере D-Wave, добавляем к “целевому” гамильтониану ${\hat{H}}_0$ (problem Hamiltonian) слагаемое, которое называется tunneling Hamiltonian:

(62)$$\hat{H}(t)={\hat{H}}_0-\mathrm{\Gamma }(t)\sum _i{\hat{\sigma }}_i^x={\hat{H}}_0+{\hat{H}}_{tun}(t),$$

где ${\hat{H}}_{tun}(t)$ зависит от времени и отвечает за квантовомеханическое туннелирование между различными собственными состояниями гамильтониана ${\hat{H}}_0$. Оператор ${\hat{H}}_{tun}(t)$ соответствует приложенному внешнему магнитному полю вдоль оси $x$ (т.е. поперечному, transverse). Когда величина $\mathrm{\Gamma }(t)$ очень велика по сравнению с $J_{ij}$ и $h$, собственное состояние гамильтониана $\hat{H}(t)$, соответствующее его минимальному собственному значению, представляет собой линейную комбинацию всевозможных состояний системы с приблизительно равными амплитудами вероятностей ориентации каждого спина вверх и вниз. Если достаточно медленно уменьшать $\mathrm{\Gamma }(t)$ с очень большой величины до нуля, можно надеяться (в соответствии с адиабатической теоремой), что приведем систему в основное состояние гамильтониана ${\hat{H}}_0$.

В обсуждаемой статье в качестве примеров рассматриваются три различных закона изменения $\mathrm{\Gamma }(t)$:

• $\mathrm{\Gamma }(t)=\frac{c}{\ln (t+1)},$

• $\mathrm{\Gamma }(t)=\frac{c}{\sqrt{t}},$

• $\mathrm{\Gamma }(t)=\frac{c}{t},$

везде $t\in (0,+\mathrm{\infty })$ и $c=\text{const}$.

Квантовая динамика системы описывается нестационарным уравнением Шредингера

(63)$$i\frac{\partial }{\partial t}|\psi (t)⟩=\hat{H}(t)|\psi (t)⟩$$

Это уравнение решается численно (с помощью дискретизации по времени и применения конечно-разностной схемы) для небольшой системы (число спинов $N=8$). Измерить близость состояния $|\psi (t)⟩$ к основному состоянию $|g⟩$ гамильтониана ${\hat{H}}_0$ можно путем вычисления вероятности

$$P_{QA}(t)={\left|⟨g|\psi (t)⟩\right|}^2$$

Note

Основное состояние $|g⟩$ для небольшого числа спинов можно найти точно, например, путем полного перебора.

Кроме того, можно рассмотреть так называемое квазистатическое приближение. Выберем какое-нибудь значение $\mathrm{\Gamma }=\text{const}$ и решим задачу об основном состоянии $|{\psi }_{\mathrm{\Gamma }}⟩$ независящего от времени гамильтониана

$${\hat{H}}_0-\mathrm{\Gamma }\sum _i{\hat{\sigma }}_i^x$$

Следует ожидать, что при очень медленном изменении $\mathrm{\Gamma }(t)$ вероятность

$$P_{QA}^{st}(\mathrm{\Gamma })={\left|⟨g|{\psi }_{\mathrm{\Gamma }}⟩\right|}^2$$

будет близка к $P_{QA}(t)$ (имеется в виду, что значение $\mathrm{\Gamma }$ соответствует значению $\mathrm{\Gamma }(t)$). Отличие $P_{QA}(t)$ от $P_{QA}^{st}(\mathrm{\Gamma })$ говорит о том, насколько близко состояния системы при динамическом процессе отжига следуют за соответствующими “квазистатическими” состояниями.

Классическая имитация отжига (SA)

В лекции, посвященной комбинаторной оптимизации, процесс имитации отжига описывался таким образом: выбиралось случайное начальное состояние, затем оно в цикле подвергалось случайной модификации, и новое состояние принималось или отклонялось в соответствии с некоторым критерием. В статье [KN98] принят другой подход к SA. Рассматривается так называемое основное кинетическое уравнение (англ. master equation). Оно описывает классический SA процесс, соответствующий нестационарному уравнению Шредингера (63). В нашем случае это система обыкновенных дифференциальных уравнений для вероятностей нахождения системы в различных состояниях $i$ в момент времени $t$:

(64)$$\frac{d{P}_i(t)}{dt}=\sum _j{\mathcal{L}}_{ij}{P}_j(t),$$

где ${\mathcal{L}}_{ij}$ – вероятность перехода системы из состояния $j$ в состояние $i$ (при $j\ne i$) в единицу времени. Рассматриваются только элементарные переходы, сопровождающиеся изменением ориентации какого-либо одного спина (остальные спины при данном переходе не меняют ориентацию). Элементы матрицы переходов записываются следующим образом:

(65)$$\begin{array}{r}{\mathcal{L}}_{ij}=\{\begin{array}{ll}\frac{1}{1+\exp \left(\frac{E_i-E_j}{T(t)}\right)}& (\text{single-spin transition},j\ne i)\\ -\sum _{k\ne i}{\mathcal{L}}_{ki}& (j=i)\\ 0& \text{(otherwise)}\end{array}\end{array}$$

Для первого условия правая часть в формуле (65) соответствует распределению Больцмана. Для понимания полезно проанализировать несколько предельных случаев:

• если $E_i<E_j$ и $|E_i-E_j|\gg T(t)$, то вероятность перехода $j\to i$ близка к 1;

• если $E_i>E_j$ и $E_i-E_j\gg T(t)$, то вероятность перехода $j\to i$ близка к 0;

• если $|E_i-E_j|\ll T(t)$, то вероятность перехода $j\to i$ близка к $1/2$.

Все случаи соответствуют интуитивным ожиданиям.

Во втором условии в (65) сама сумма (без знака “минус”) равна суммарной вероятности перехода из состояния $i$ во все остальные состояния. Так что эта сумма должна входить со знаком “минус” в выражение $\frac{d{P}_i(t)}{dt}$ для темпа изменения вероятности $P_i$ нахождения в состоянии $i$.

Третье условие в (65) означает, что рассматриваем только перевороты одиночных спинов (single-spin flip) в качестве допустимых переходов между состояниями системы.

Зависимость температуры от времени выбирается равной $\mathrm{\Gamma }(t)$:

$$T(t)=\mathrm{\Gamma }(t)$$

Близость решения задачи SA к основному состоянию $|g⟩$ гамильтониана ${\hat{H}}_0$ выражается величиной вероятности $P_g(t)$ найти систему в основном состоянии в момент времени $t$:

$$P_{SA}(t)=P_g(t)$$

Аналогично квантовому случаю, введем величину $P_{SA}^{st}(T)$, которая в квазистатическом приближении близка к $P_{SA}(t)$ (если величина температуры $T=T(t)$).

Анализ и сравнение результатов

В статье обсуждаются численные результаты для $P_{SA}$ и $P_{QA}$ для различных конфигураций обменного взаимодействия и различных вариантов зависимости поперечного поля от времени. В всех случаях продольное внешнее поле выбрано постоянным: $h=0.1$.

Ферромагнитная модель

Здесь проводится численный эксперимент для ферромагнитной модели Изинга с $J_{ij}=\text{const}$ для всех пар спинов. Зависимости $T$ и $\mathrm{\Gamma }$ от времени выбираются такими:

$$\mathrm{\Gamma }(t)=T(t)=\frac{3}{\ln (t+1)}$$

Результаты представлены на Fig. 107.

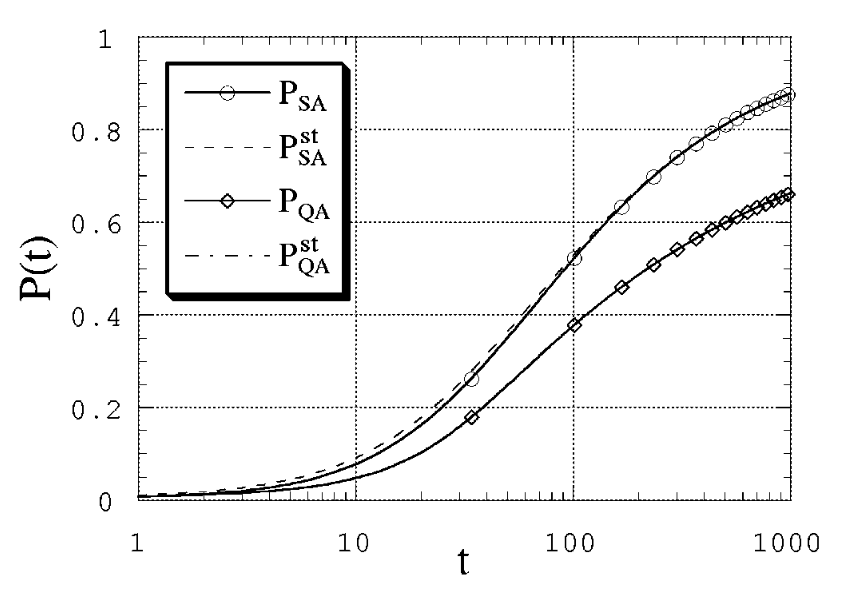
Fig. 107 Зависимости $P_{SA}(t)$, $P_{QA}(t)$, $P_{SA}^{st}(T(t))$ и $P_{QA}^{st}(\mathrm{\Gamma }(t))$ для ферромагнитной модели при $\mathrm{\Gamma }(t)=T(t)=3/\ln (t+1)$.

Видно, что квазистатическое приближение работает очень хорошо, интересующие нас величины в динамическом процессе очень близки к вычисленным в равновесных условиях. Когда расписание отжига имеет вид $T(t)=c/\ln (t+1)$, гарантируется сходимость $P_{SA}\to 1$ при подходящем выборе константы $c$ (в статье [KN98] есть ссылка на соответствующую теорему). Выбор константы $c=3$ достаточно произволен, но высокая точность приближенного равенства $P_{SA}(t)\approx P_{SA}^{st}(T(t))$ свидетельствует о том, что в рассматриваемом случае действительно $P_{SA}\to 1$ при $t\to +\mathrm{\infty }$.

Для QA нет аналогичного точного утверждения о сходимости $P_{QA}\to 1$, но численные результаты для данного ферромагнитного случая при $\mathrm{\Gamma }(t)=3/\ln (t+1)$ позволяют предположить такую сходимость.

Тот факт, что QA-кривая на Fig. 107 всегда ниже SA-кривой, никакого значения не имеет, потому что в обеих задачах у нас все величины обезразмерены ($\hslash =1$ в (63) и единица времени $\tau =1$ в (64)) и никакого согласования при обезразмеривании в двух задачах нет.

Если уменьшать поперечное поле и температуру быстрее,

$$\mathrm{\Gamma }(t)=T(t)=\frac{3}{\sqrt{t}},$$

то возникает качественное отличие QA и SA решений, см. Fig. 108.

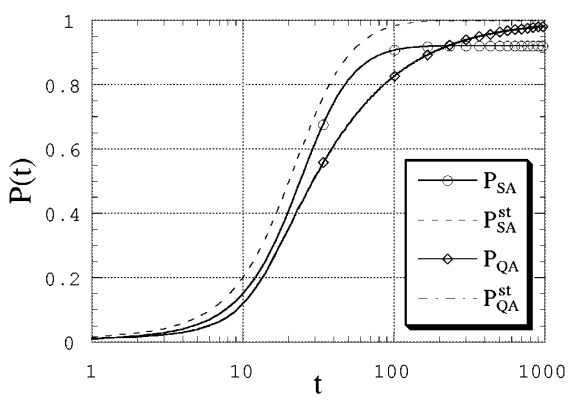
Fig. 108 Вид коэффициентов перекрытия для ферромагнитной модели при $\mathrm{\Gamma }(t)=T(t)=3/\sqrt{t}$.

Видно, что решение квантовомеханической задачи лучше сходится к основному состоянию, чем решение классической задачи. Более того, SA-решение “застревает” в каком-то локальном минимуме с не очень малой вероятностью. На Fig. 109 виден темп приближения $P_{QA}$ к 1 (на графике двойная логарифмическая шкала). Можно сделать вывод, что $(1-P_{QA})\propto 1/t$ в широком диапазоне $t$.

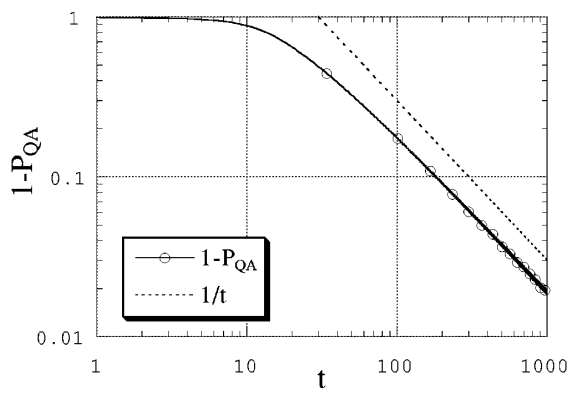
Fig. 109 $(1-P_{QA}(t))$ для ферромагнитной модели при $\mathrm{\Gamma }(t)=3/\sqrt{t}$.

Если еще быстрее уменьшать поперечное поле и температуру,

$$\mathrm{\Gamma }(t)=T(t)=\frac{3}{t},$$

то оба решения “застревают” в неосновных состояниях, как видно из Fig. 110.

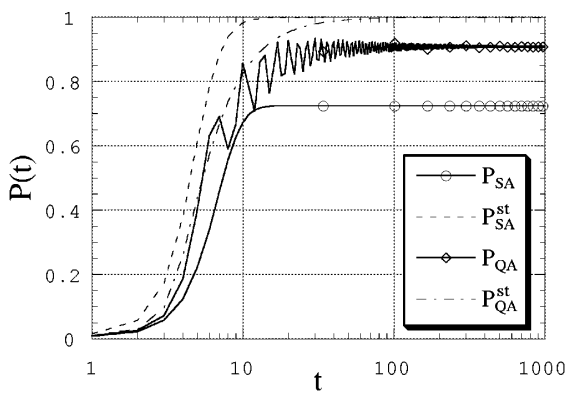
Fig. 110 Вид коэффициентов перекрытия для ферромагнитной модели при $\mathrm{\Gamma }(t)=T(t)=3/t$.

Фрустрированная модель

Здесь анализируется так называемая фрустрированная (frustrated) система, она изображена на Fig. 111.

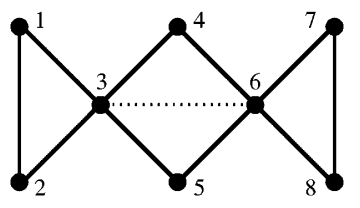
Fig. 111 Фрустрированная система спинов.

Сплошные линии обозначают ферромагнитное взаимодействие между спинами, пунктирная линия – антиферромагнитное взаимодействие (сила которого по абсолютной величине равна силе ферромагнитного взаимодействия). Если в SA-задаче температура очень велика, то спины 4 и 5 меняют свою ориентацию с очень высокой частотой, так что взаимодействие спинов 3 и 6 посредством спинов 4 и 5 пренебрежимо мало. В этом случае прямое антиферромагнитное взаимодействие между спинами 3 и 6 оказывается доминирующим, поэтому наблюдается отрицательная корреляция между ориентациями спинов 3 и 6 (см. Fig. 112).

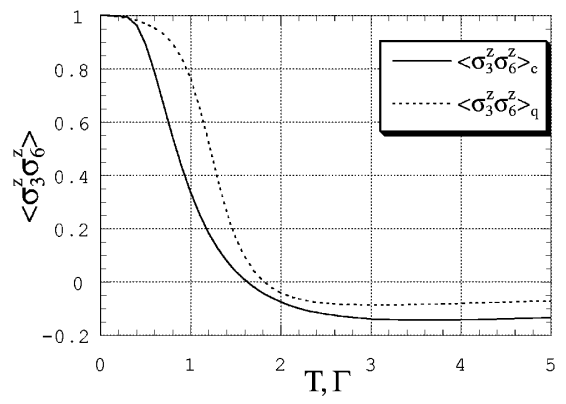
Fig. 112 Величина корреляции спинов 3 и 6. Индекс c означает классическое решение (SA), индекс q означает квантовомеханическое решение (QA).

С другой стороны, при низкой температуре спины 4 и 5 стремятся принять определенную устойчивую ориентацию. В этом случае эффективное (непрямое) ферромагнитное взаимодействие между спинами 3 и 6 посредством спинов 4 и 5 примерно вдвое сильнее, чем прямое антиферромагнитное взаимодействие. Эти рассуждения подтверждаются положительной величиной корреляции ${⟨{\sigma }_3^z{\sigma }_6^z⟩}_c$ при низких температурах (Fig. 112). Значит, спины 3 и 6 должны поменять взаимную ориентацию при некоторой промежуточной температуре.

Если поперечное поле в QA-задаче играет роль, аналогичную роли температуры в SA-задаче, то следует ожидать схожего поведения величины корреляции ${⟨{\sigma }_3^z{\sigma }_6^z⟩}_q$ при изменении $\mathrm{\Gamma }$. Здесь наблюдаемая ${⟨{\sigma }_3^z{\sigma }_6^z⟩}_q$ вычисляется с использованием основного состояния гамильтониана (62) при заданной $\mathrm{\Gamma }$. Так и есть (см. пунктирную кривую на Fig. 112).

Если использовать расписание отжига

$$\mathrm{\Gamma }(t)=T(t)=\frac{3}{\sqrt{t}},$$

то получаются результаты, изображенные на Fig. 113.

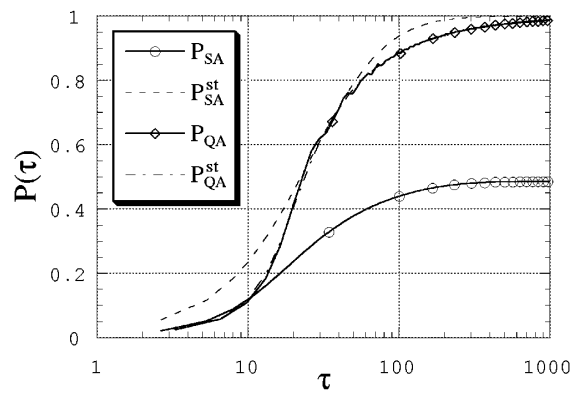
Fig. 113 Вид коэффициентов перекрытия для фрустрированной модели при $\mathrm{\Gamma }(t)=T(t)=3/\sqrt{t}$.

Обезразмеренное время $\tau =t{T}_c^2$ для SA-задачи и $\tau =t{\mathrm{\Gamma }}_c^2$ для QA-задачи. Здесь $T_c$ и ${\mathrm{\Gamma }}_c$ – критические величины, при которых ${⟨{\sigma }_3^z{\sigma }_6^z⟩}_c$ и ${⟨{\sigma }_3^z{\sigma }_6^z⟩}_q$ переходят через ноль на графике Fig. 112. Видно, что квантовый отжиг лучше подходит для поиска основного состояния в такой системе.

Модель со случайными взаимодействиями

Последний рассмотренный пример – это модель спинового стекла, предложенная Шеррингтоном и Киркпатриком [SK75]. Для всех пар спинов есть взаимодействие, сила которого является случайной величиной и семплируется из гауссова распределения с нулевым средним и с дисперсией $1/N$ (в нашем случае $N=8$). На Fig. 114 показан типичный результат для эволюции коэффициентов перекрытия во времени при расписании отжига $\mathrm{\Gamma }(t)=T(t)=3/\sqrt{t}$.

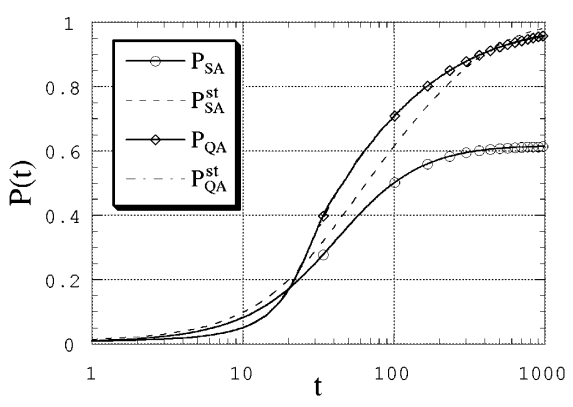
Fig. 114 Вид коэффициентов перекрытия для модели Шеррингтона-Киркпатрика при $\mathrm{\Gamma }(t)=T(t)=3/\sqrt{t}$.

Было проверено несколько реализаций для коэффициентов обменного взаимодействия (семплирование выполнялось из одной и той же функции распределения), результаты оказались качественно близкими. Графики на Fig. 114 подтверждают, что для данной оптимизационной задачи квантовый отжиг подходит лучше, чем классический.

Заключение

В этой лекции рассказали о канонической работе, в которой для модели Изинга рассмотрены классическая имитация отжига и квантовая имитация отжига, выполнен анализ и сравнение свойств решений в рамках этих двух подходов на нескольких примерах. Выяснилось, что:

• при одном и том же расписании отжига квантовый отжиг дает сходимость к основному состоянию с большей вероятностью, чем классический отжиг;

• для квантового случая система сходится к основному состоянию при расписании отжига $\mathrm{\Gamma }=c/\sqrt{t}$, но не при более быстром уменьшении поперечного поля;

• для ферромагнитной модели при квантовом отжиге вероятность получения основного состояния ведет себя приближенно как $(1-\frac{\text{const}}{t})$ на больших временах $t$.