Практика VQE
Contents
Практика VQE#
Автор(ы):
Эта лекция будет посвящена практике с VQE, а именно решению задачи коммивояжера. Будет много кода и мало теории. Рекомендуется заранее повторить следующие лекции:
Описание задачи коммивояжера в лекции про задачи комбинаторной оптимизации.
Сведение этой задачи к модели Изинга в лекции о переходе от комбинаторных задач к квантовым алгоритмам.
Нам потребуется определить бинарный оператор \(\sigma^{z_{mod}}\), который активно использовали при определении гамильтониана. Нужно будет расписать полный оператор, отвечающий данной задаче и нужен случайный взвешенный граф, по которому будет “путешествовать” коммивояжер. Начнем с импорта библиотек и генерации графа.
Импорт библиотек#
Для графов будем использовать структуры данных из уже знакомой нам библиотеки NetwrokX, а для работы с разреженными операторами SciPy.
import matplotlib.pyplot as plt
%config InlineBackend.figure_format = "retina"
import numpy as np
import networkx as nx
from scipy import sparse
from scipy.sparse import linalg as sl
Случайный взвешенный граф#
Случайный взвешенный граф проще всего сгенерировать из случайной матрицы весов. Давайте сделаем такую:
Note
Тут будем работать с матрицей полного графа, то есть такого, в котором каждая вершина связана с каждой. Это вполне корректное допущение для задачи коммивояжера, так как, например, из каждого города РФ обычно можно попасть во все другие, пусть и за разное время в пути.
np.random.seed(42)
rand_mat = np.random.randint(0, 100, (4, 4))
Только эта матрица не является симметричной и имеет ненулевые элементы на диагонали. Элементы на диагонали означают петли (loop или self-loop), что не очень разумно в терминах задачи коммивояжера: не ясно, что значит, например, путь из Москвы в Москву. Аналогично и про то, что матрица не симметричная: если путь из Москвы в Санкт-Петербург займет 6 часов, то и путь обратно тоже займет столько же. Так что хотим симметричную матрицу. Давайте это исправим:
rand_adj = (rand_mat + rand_mat.T) / 2
np.fill_diagonal(rand_adj, 0)
Наконец, сделаем из этого граф и визуализируем его:
g = nx.Graph(rand_adj)
pos = nx.drawing.layout.random_layout(g, seed=42)
nx.draw(g, pos=pos)
edge_weights = nx.get_edge_attributes(g, "weight")
nx.draw_networkx_edge_labels(g, pos=pos, edge_labels=edge_weights)
nx.draw_networkx_labels(g, pos=pos)
plt.show()
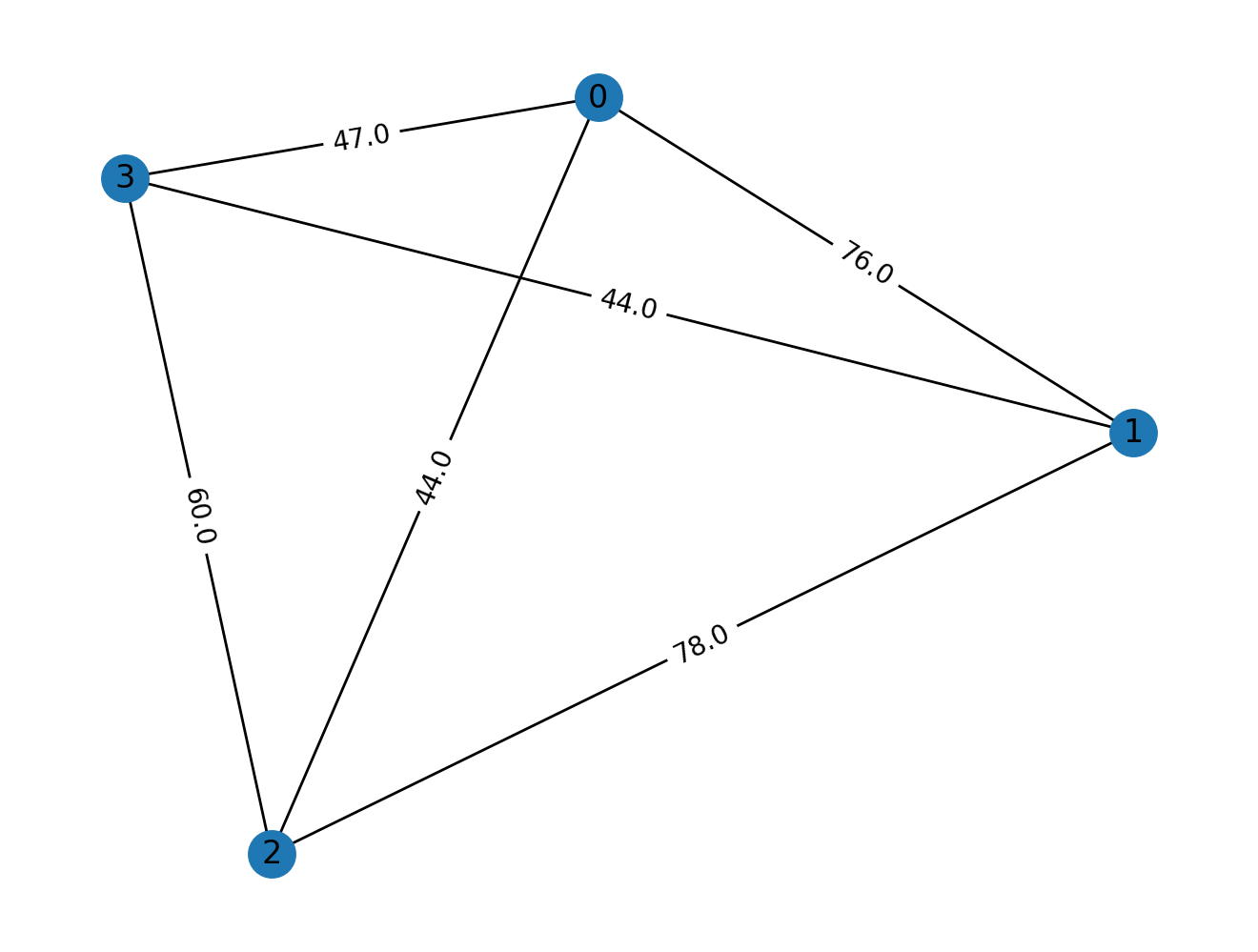
Решение задачи TSP в NetworkX#
Для того, чтобы потом понять, что все правильно сделали, давайте найдем приближенное решение задачи средствами NetworkX.
nx_solution = nx.algorithms.approximation.traveling_salesman_problem(g)
print(f"NetworkX solution (nodes order): {nx_solution}")
nx_solution_cost = 0
for i in range(len(nx_solution) - 1):
nx_solution_cost += g.get_edge_data(nx_solution[i], nx_solution[i + 1])["weight"]
print(f"NetworkX solution (total cost): {nx_solution_cost}")
NetworkX solution (nodes order): [0, 3, 1, 2, 0]
NetworkX solution (total cost): 213.0
Матрица \(\sigma^z_{mod}\)#
Это бинарный оператор, который ранее вводили в лекции о представлении комбинаторных задач в виде моделей Изинга. Соотношение между \(\sigma^z_{mod}\) и \(\sigma^z\) таково:
def sigma_z_mod(k: int, size: int) -> sparse.csr_matrix:
sz_mod = sparse.coo_matrix(
[
[1, 0,],
[0, 0,],
]
)
left_ith = sparse.eye(2 ** k, format="coo")
right_ith = sparse.eye(2 ** (size - k - 1), format="coo")
return sparse.kron(
sparse.kron(left_ith, sz_mod),
right_ith,
)
Для произвольного состояния \(\ket{\psi}\) справедливо
Пусть \(\ket{\phi}\) – собственный вектор (собственное состояние) оператора \(\hat{\sigma}^z\), соответствующий собственному значению \(\lambda\):
Отсюда следует, что
Значит,
собственные векторы \(\hat{\sigma}^z_{mod}\) и \(\hat{\sigma}^z\) совпадают;
соответствующие собственные значения связаны соотношением \(\lambda_{mod} = \frac{1 + \lambda}{2}\).
Поскольку \(\lambda \in \{-1, +1\}\), получаем \(\lambda_{mod} \in \{0, 1\}\). На всякий случай проверим это, создав оператор маленькой размерности и вычислив его собственные значения:
eigs = np.linalg.eig(sigma_z_mod(1, 3).toarray())
print(np.unique(eigs[0]))
[0. 1.]
Напомню, что у нас zero-based индексация, поэтому sigma_z_mod(1, 3) значит что-то типа “построй мне матрицу \(\hat{\sigma}^z_{mod}\), действующую на второй спин (ну или второй кубит)”.
Легко убедиться, что
для \(\lambda_{mod} = 1\) собственный вектор представляется битовой строкой, в которой спин с индексом 1 имеет значение 0;
для \(\lambda_{mod} = 0\) собственный вектор представляется битовой строкой, в которой спин с индексом 1 имеет значение 1.
def sigmaz_k(k: int, n: int) -> sparse.csr_matrix:
left_part = sparse.eye(2 ** k)
right_part = sparse.eye(2 ** (n - 1 - k))
return sparse.kron(
sparse.kron(
left_part,
sparse.csr_matrix(np.array([[1, 0,], [0, -1,],]))
),
right_part
)
def probs2bit_str(probs: np.array) -> str:
size = int(np.log2(probs.shape[0]))
bit_s_num = np.where(probs == probs.max())[0][0]
s = f"{bit_s_num:b}"
s = "0" * (size - len(s)) + s
return s
for i, psi in enumerate(eigs[1]):
probs = psi * psi.conj()
bit_s = probs2bit_str(probs)
print(f"Eigenvalue: {eigs[0][i]}\tBit string: {bit_s}")
Eigenvalue: 1.0 Bit string: 000
Eigenvalue: 1.0 Bit string: 001
Eigenvalue: 0.0 Bit string: 010
Eigenvalue: 0.0 Bit string: 011
Eigenvalue: 1.0 Bit string: 100
Eigenvalue: 1.0 Bit string: 101
Eigenvalue: 0.0 Bit string: 110
Eigenvalue: 0.0 Bit string: 111
Убедимся также в совпадении собственных векторов с матрицей \(\sigma^z\):
Note
Для чистых состояний без запутывания матрицы собственных векторов могут быть приведены к виду единичных матриц. И действительно, каждый собственный вектор отвечает строго одной конфигурации спинов, а значит его волновая функция имеет вид \(\ket{\Psi} = \ket{0, 0, ..., 1, ..., 0, 0}\), где 1 соответствует как раз номеру той битовой строки, которая отвечает этой конфигурации.
print(f"Sigma z_mod:\n{eigs[1]}")
print(f"\nSigma z:\n{np.linalg.eig(sigmaz_k(1, 3).toarray())[1]}")
Sigma z_mod:
[[1. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 0. 0. 1.]]
Sigma z:
[[1. 0. 0. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0.]
[0. 0. 1. 0. 0. 0. 0. 0.]
[0. 0. 0. 1. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0.]
[0. 0. 0. 0. 0. 1. 0. 0.]
[0. 0. 0. 0. 0. 0. 1. 0.]
[0. 0. 0. 0. 0. 0. 0. 1.]]
Note
В общем случае, даже если у двух операторов совпадают собственные вектора, то их порядок (по возрастанию собственных значений) совпадать совсем не обязан. В этом легко убедиться, например, если поменять местами \(\hat{1}\) и \(\hat{\sigma^z}\) в \(\sigma^{z_{mod}}\). Поэтому, чтобы избежать ошибок в будущем, лучше не привыкать сравнивать матрицы собственных векторов при помощи np.allclose, а сравнивать их глазами построчно.
Гамильтониан задачи TSP#
Давайте еще раз выпишем полный гамильтониан системы. Напомню, что задача будет параметризована при помощи \(N^2\) кубит, которые для удобства выстроены в виде матрицы, где \(i\)-я строка соответствует \(i\)-му шагу в цикле по графу, а \(j\)-й элемент строки соответствует номеру вершины и является бинарным оператором:
Note
Еще раз вспомним, что первые два слагаемых “говорят”: каждая вершина должна входить только в один столбец, а каждая строка должна содержать только одну вершину. Третье слагаемое представляет собой штраф за соединение вершин, между которыми нет ребра, а четвертое дает стоимость всего пути. Первые три слагаемых идут с бОльшим коэффициентом, чем последнее, так как нам важно в первую очередь получить реальное решение, а не получить самое дешевое.
Сделаем финт ушами: будем всегда считать, что путь коммивояжера начинается в вершине с индексом 0. Так как путь коммивояжера это гамильтонов цикл, то делаем это упрощение без какой-либо потери общности, так как вершина с индексом 0 все равно должна будет войти в путь. При этом такой хитрый трюк позволит снизить число необходимых кубит с \(N^2\) до \((N - 1)^2\), что довольно существенно (хотя асимптотическая сложность остается такой же). Работать с графом будем при помощи уже знакомой библиотеки NetworkX:
def convert_tsp_to_ising(g: nx.Graph) -> sparse.coo_matrix:
# Имеется два элемента гамильтониана:
# - часть, дающая нам Гамилтонов цикл
# - часть, считающая стоимость пути
# Для нас важно, чтобы вес первой части превалирвал.
# Поэтому, в качестве коэффициента берем
# пятикратное значение максимального веса ребер в графе.
a = 5 * max([e[2]["weight"] for e in g.edges(data=True)])
size = g.number_of_nodes() - 1
H = sparse.coo_matrix((2 ** (size ** 2), 2 ** (size ** 2)), dtype=np.complex128)
# Вычисляем сумму по колонкам:
# - каждая вершина должна быть в каждой колонке строго один раз
for i in range(size):
# Считаем выражение 1 - sum
col_sum = sparse.eye(2 ** (size ** 2), format="coo")
for j in range(size):
col_sum -= sigma_z_mod(i + j * size, size ** 2)
# Возводим в квадрат и добавляем к гамилтониану
H += a * col_sum * col_sum
# Вычисляем сумму по строкам:
# - каждая вершина должна быть в каждой строке строго один раз
for j in range(size):
row_sum = sparse.eye(2 ** (size ** 2), format="coo")
for i in range(size):
row_sum -= sigma_z_mod(i + j * size, size ** 2)
# Аналогично, в квадрат и добавляем
H += a * row_sum * row_sum
# Считаем сумму по тем ребрам, которых в графе нет и тем, которые есть.
for i in range(size):
for j in range(size):
if g.has_edge(i + 1, j + 1):
# Сумма по всем ребрам графа
coef = g.get_edge_data(i + 1, j + 1)["weight"]
else:
# Сумма по всем отсутствующим ребрам графа
coef = a
for k in range(size - 1):
# Дальше просто используем полученный коэффициент и считаем сумму
H += (
coef
* sigma_z_mod(i + k * size, size ** 2)
* sigma_z_mod(j + (k + 1) * size, size ** 2)
)
H += (
coef
* sigma_z_mod(i + (size - 1) * size, size ** 2)
* sigma_z_mod(j, size ** 2)
)
# Начинаем всегда из нулевой вершины, это позволяет снизить число необходимых кубитов.
# Теперь должны добавить в гамильтониан слагаемое, отвечающее за нулевую вершину в пути.
for j in range(size):
if g.has_edge(0, j + 1):
coef = g.get_edge_data(0, j + 1)["weight"]
else:
coef = a
H += coef * sigma_z_mod(j, size ** 2)
H += coef * sigma_z_mod(j + (size - 1) * size, size ** 2)
# PennyLane работает с матрицами только в координатном формате, поэтому сразу делаем приведение.
return sparse.coo_matrix(H)
Убедимся, что точное решение даст тот же путь (с той же стоимостью), что и решение из NetworkX:
op = convert_tsp_to_ising(g)
scipy_solution = sl.eigs(op, k=1, which="SR", return_eigenvectors=True)
print(f"Ground state energy: {scipy_solution[0][0]:.4f}")
probs = scipy_solution[1] * scipy_solution[1].conj()
bit_s = probs2bit_str(probs)
# Нулевая вершина всегда первая
scipy_path = [0,]
for i in range(3):
k = 0
for j in range(3):
if bit_s[j + i * 3] == "0":
k = j + 1
scipy_path.append(k)
scipy_path.append(0)
scipy_solution_cost = 0
for i in range(len(scipy_path) - 1):
scipy_solution_cost += g.get_edge_data(scipy_path[i], scipy_path[i + 1])["weight"]
print(f"SciPy solution (nodes order): {scipy_path}")
print(f"SciPy solution (total cost): {scipy_solution_cost}")
Ground state energy: 273.0000-0.0000j
SciPy solution (nodes order): [0, 2, 1, 3, 0]
SciPy solution (total cost): 213.0
Видим, что решение через матрицу совпадает с тем, что выдал NetworkX (с точностью до инверсии: [0, 2, 1, 3, 0] и [0, 3, 1, 2, 0]), как и общая стоимость пути. Энергия основного состояния отличается по причине того, что использовали оптимизацию и магию с коэффициентами. Но это не так важно: по энергиям важно лишь отношение порядка, потому что зная битовую строку всегда можем проверить стоимость пути за линейное время!
Теперь можно наконец-то, приступать к симуляции квантовых вычислений!
VQE на Pennylane#
Для начала давайте преобразуем матрицу к тому объекту, с которым умеет работать квантовый фреймворк.
Note
Pennylane поддерживает также работу с представлением гамильтонианов в виде так называемых Паули-строк, но тут не будем еще раз определять весь гамильтониан, а просто перериспользуем разреженную матрицу.
Веса графа имеют разброс значений от 0 до 100. Из-за этого, при некоторых конфигурациях можем получать очень большое собственное значение гамильтониана, вплоть до нескольких тысяч. Это не очень хорошо для градиентного спуска методом paramter-shift, поэтому для численной устойчивости давайте умножим все значения весов на \(0.1\). Это сделает градиенты не слишком большими и улучшит численную устойчивость. Делать это можно совершенно спокойно, так как не критична численная величина минимального собственного, а важно лишь отношение порядка собственных значений.
import pennylane as qml
numer_stability_const = 0.1
ham = qml.SparseHamiltonian(op * numer_stability_const, wires=list(range(9)))
/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
warnings.warn("Setuptools is replacing distutils.")
Далее необходимо выбрать ansatz. Современные квантовые процессоры обычно имеют вид решетки, типа такого:
Fig. 100 Схематичное изображение квантового компьютера Sycamore от компании Google [AAB+19]#
Поэтому, в идеале, хотелось бы делать либо однокубитные операции, либо двухкубитные операции, но над “соседними” кубитами. Так появилась идея hardware efficient ansatz [KMT+17]. Он заключается в том, что формируется несколько “слоев” VQC, где каждый такой слой содержит несколько операций вращений, а также попарные “запутывающие” операции (например, CZ, или гейт CNOT). Выглядит это примерно так:
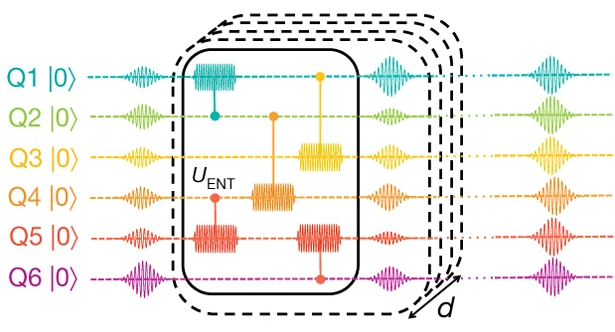
Fig. 101 Иллюстрация hardware efficient ansatz (HWEA) из [KMT+17]#
Давайте реализуем такой слой:
size = len(ham.wires)
def layer(params):
for i in range(size):
qml.RY(params[i][0], wires=i)
qml.RZ(params[i][1], wires=i)
for i in range(size - 1):
qml.CZ(wires=[i, i + 1])
Здесь специально не повторяем основ параметризированных квантовых схем. Для тех, кто забыл, что это такое, рекомендуем вернуться к отдельной лекции по этой теме.
Теперь создадим устройство, которое будет квантовым симулятором, а также напишем код, который будет на этом устройстве запускаться. Такой код должен последовательно применить несколько HWEA слоев, после чего измерить ожидаемое значение гамильтониана в полученном состоянии.
device = qml.device("default.qubit", wires=size)
num_layers = 3
@qml.qnode(device, diff_method="parameter-shift")
def feed_forward(params, wires=size):
for k in range(3):
layer(params[k])
for i in range(size):
qml.RY(params[-1][i][0], wires=i)
qml.RZ(params[-1][i][1], wires=i)
return qml.expval(ham)
Теперь надо сгенерировать параметры и выбрать метод их оптимизации. В этот раз давайте воспользуемся алгоритмом Momentum, так называемым “ускоренным” градиентным спуском:
opt = qml.MomentumOptimizer()
params = tuple(
tuple(
(
np.random.rand() * 2 * np.pi,
np.random.rand() * 2 * np.pi,
)
for _ in range(size)
)
for _ in range(num_layers + 1)
)
Ну и наконец можно приступать к оптимизации параметров. Все примерно также, как в базовой лекции про градиенты. То есть ничего нового тут по сути не делается.
Симуляция#
Warning
Осторожно, следующий код работает несколько минут, так как обучаем довольно тяжелую схему на 9-и кубитах! Кстати, при желании можно добиться гораздо больше точности по энергии относительно точного решения. Для этого достаточно установить число эпох \(\sim 150\). Но поскольку этот код исполняется при сборке данных лекций, то мы не можем себе позволить считать отдельные страницы по 7-10 минут. Читателю рекомендуется самостоятельно определить то число эпох, которого достаточно, чтобы получить точность в 3-м знаке после запятой.
energy = [
feed_forward(params),
]
for epoch in range(85):
params, e = opt.step_and_cost(feed_forward, params)
energy.append(e)
if epoch % 5 == 0:
print(f"epoch: {epoch}\tenergy: {e:.6f}")
/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/pennylane/_grad.py:95: UserWarning: Starting with PennyLane v0.21.0, when using Autograd, inputs have to explicitly specify requires_grad=True (or the argnum argument must be passed) in order for trainable parameters to be identified.
warnings.warn(
epoch: 0 energy: 360.638506
epoch: 5 energy: 163.172963
epoch: 10 energy: 96.375950
epoch: 15 energy: 56.524352
epoch: 20 energy: 43.497589
epoch: 25 energy: 35.938162
epoch: 30 energy: 31.882151
epoch: 35 energy: 29.457526
epoch: 40 energy: 29.232270
epoch: 45 energy: 28.058306
epoch: 50 energy: 27.814023
epoch: 55 energy: 27.495886
epoch: 60 energy: 27.479515
epoch: 65 energy: 27.411348
epoch: 70 energy: 27.348231
epoch: 75 energy: 27.329692
epoch: 80 energy: 27.324815
plt.figure(figsize=(10, 8))
plt.plot(np.arange(len(energy)), energy, ".-", label="Energy by epochs")
plt.hlines(
np.real(scipy_solution[0][0]) * numer_stability_const,
0,
len(energy),
color="red",
label="Exact solution",
)
plt.xlabel("Epoch")
plt.ylabel("Energy")
plt.legend()
plt.show()
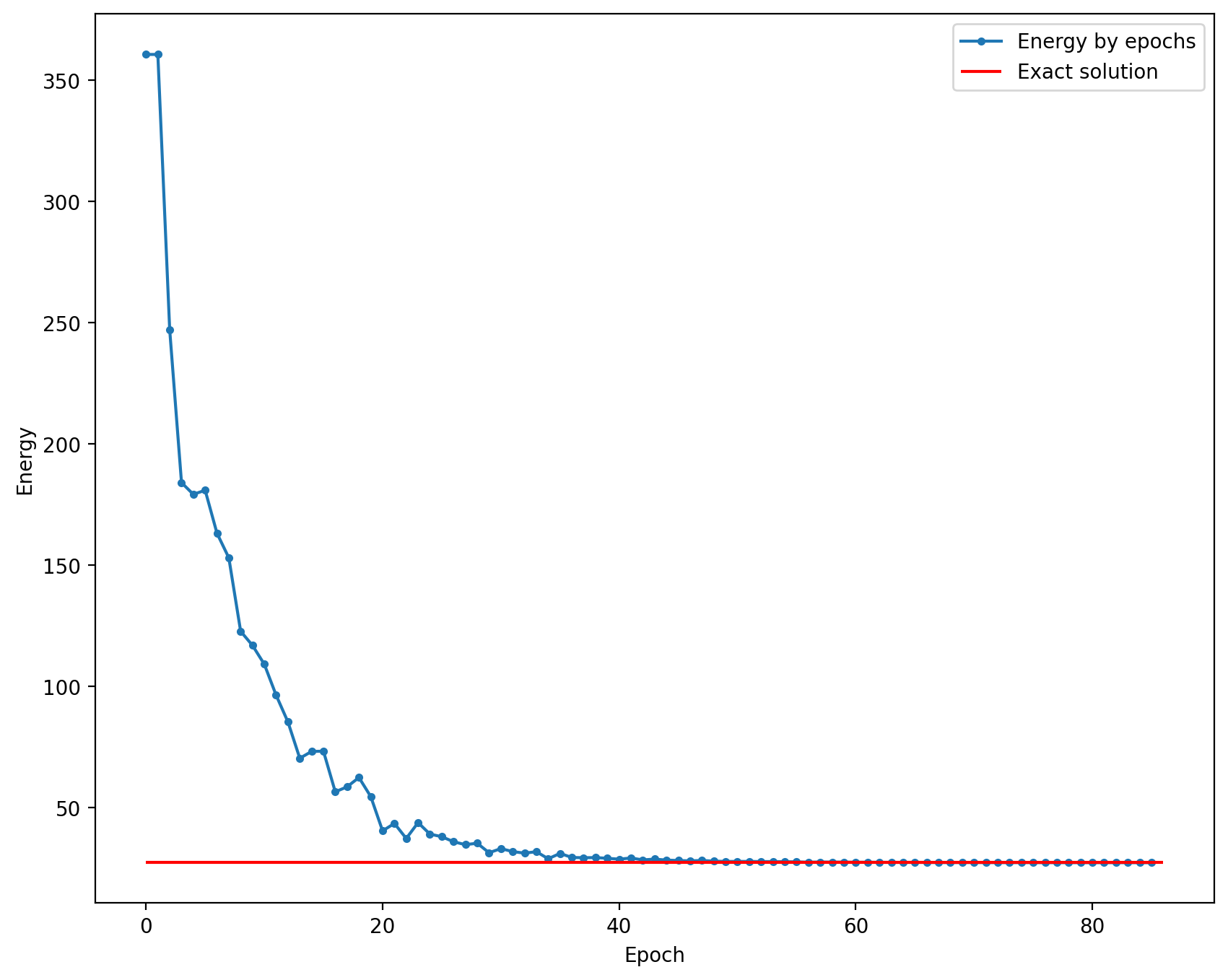
Видим, что VQE отлично сходится к основному состоянию, которое знаем из SciPy и ARPACK. Теперь давайте убедимся, что квантовый путь совпадет с тем, что получили из NetworkX. Для этого нужно получить распределение вероятностей битовых строк. На реальном компьютере это можно сделать просто измеряя много раз, но на симуляторе есть возможность получить его сразу одной командой.
@qml.qnode(device, diff_method="parameter-shift")
def answer(params, wires=size):
for k in range(num_layers):
layer(params[k])
for i in range(size):
qml.RY(params[-1][i][0], wires=i)
qml.RZ(params[-1][i][1], wires=i)
return qml.probs(wires=list(range(size)))
probs = answer(params)
bit_s = probs2bit_str(probs)
# Нулевая вершина всегда первая
q_path = [0,]
for i in range(3):
k = 0
for j in range(3):
if bit_s[j + i * 3] == "0":
k = j + 1
q_path.append(k)
q_path.append(0)
q_solution_cost = 0
for i in range(len(q_path) - 1):
q_solution_cost += g.get_edge_data(q_path[i], q_path[i + 1])["weight"]
print(f"Quantum solution (nodes order): {q_path}")
print(f"Quantum solution (total cost): {q_solution_cost}")
Quantum solution (nodes order): [0, 2, 1, 3, 0]
Quantum solution (total cost): 213.0
Ура, получился тот же ответ, что и в SciPy/NetworkX. Значит самописный VQE работает правильно.
Заключение#
В этой лекции попрактиковались в решение реальных задач при помощи алгоритма VQE.