Cirq & TFQ#

Автор(ы):

Синченко Семен

Введение#

Cirq – это библиотека для работы с квантовыми компьютерами и симуляторами компании Google. В рамках темы квантового машинного обучения нам также интересен фреймворк Tensorflow Quantum или сокращенно TFQ. Это высокоуровневая библиотека, которая содержит готовые функции для квантового и гибридного машинного обучения. В качестве системы автоматического дифференцирования, а также для построения гибридных квантово-классических нейронных сетей там используется библиотека Tensorflow.

Warning

Во всех дальнейших лекциях мы будем использовать в основном библиотеку PennyLane, так что данная лекция исключительно обзорная и факультативная. В ней мы посмотрим несколько примеров end2end обучения квантовых схем на TFQ без детального объяснения теории и вообще того, что происходит. Основная цель данной лекции – исключительно обзор еще одного инструмента, а не изучение QML! Заинтересованный читатель может вернуться к этому обзору после изучения глав про VQC, Градиенты и Квантовые нейросети.

Работа с кубитами#

Импорты и схема#

Warning

Tensorflow Quantum нельзя установить на Windows. Если система POSIX-совместимая и хотите попробовать запустить примеры кода из этой лекции, то просто в корне данного репозитория наберите команду (если уже установили tensorflow):

poetry run pip install tensorflow-quantum==0.5.1

Обладателям компьютеров на системе Windows можем лишь предложить использовать WSL2 или Docker. В целом эта лекция факультативная и нигде далее TFQ не используется.

А так, больше информации по установке можно найти в разделе про установку в официальной документации или у них же на GitHub.

Для начала импортируем cirq.

import cirq

Cirq рассчитан на работу с квантовым компьютером от компании Google, который представляет собой решетку кубитов. Например, вот так выглядит решетка кубитов квантового компьютера Sycamore:

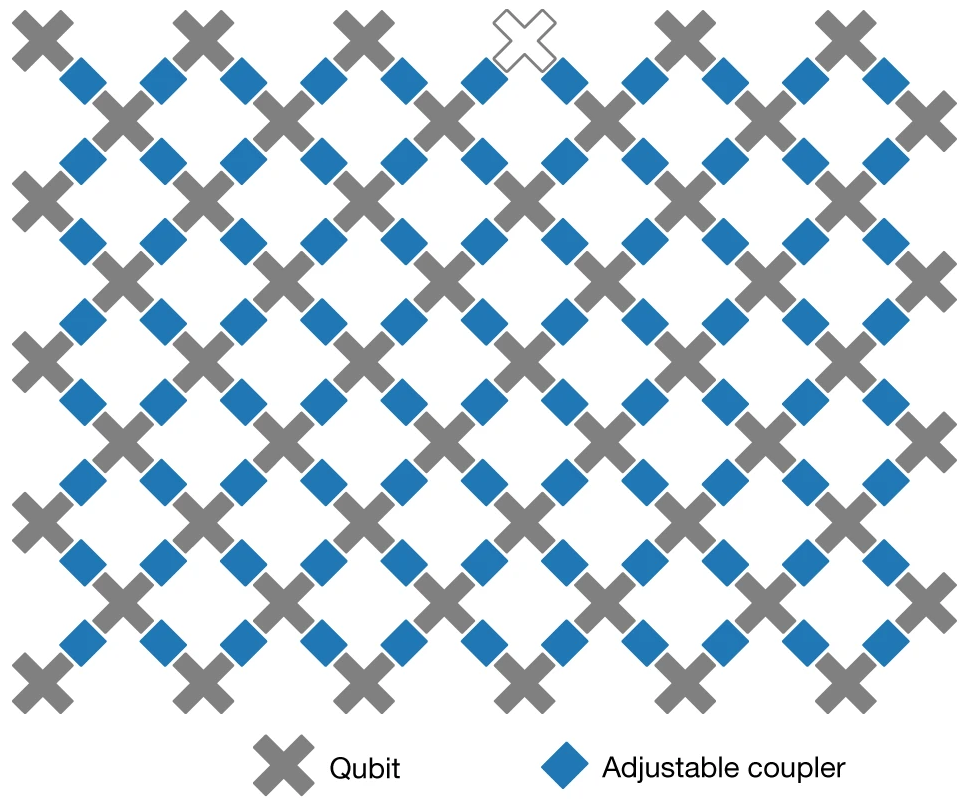
../../../_images/sycamore.png — Fig. 27 Изображение из [AAB+19]#

Поэтому в нем все строится вокруг работы с решеткой кубитов – объектом cirq.GridQubit. Давайте создадим кубит на решетке, который имеет координаты \((0, 0)\):

qubit = cirq.GridQubit(0, 0)

Следующей важной концепцией в Cirq является непосредственно квантовая схема. Давайте создадим схему, которая переводит кубит в суперпозицию состояний \(\ket{0}\) и \(\ket{1}\) и измеряет его:

circuit = cirq.Circuit()
circuit.append(cirq.H(qubit))
circuit.append(cirq.measure(qubit))
print(circuit)

(0, 0): ───H───M───

Запуск и симуляция#

Теперь создадим квантовый симулятор, который посчитает нам результат этой простой схемы на классическом компьютере:

sim = cirq.Simulator()

Как мы знаем, результат измерения такой схемы равен 50% для состояния \(\ket{0}\), то есть если мы будем сэмплировать, то должны получать \(\sim 0.5\). Проверим это с разным числом сэмплов:

print(f"5 сэмплов: {sim.sample(circuit, repetitions=5).mean()}")
print(f"\n100 сэмплов: {sim.sample(circuit, repetitions=100).mean()}")
print(f"\n1000 сэмплов: {sim.sample(circuit, repetitions=1000).mean()}")

5 сэмплов: (0, 0)    0.8
dtype: float64

100 сэмплов: (0, 0)    0.5
dtype: float64

1000 сэмплов: (0, 0)    0.471
dtype: float64

Note

Метод sim.sample возвращает хорошо знакомый всем специалистам в области Data Science объект pandas.DataFrame.

Также у нас есть опция запустить схему через метод run. Может показаться, что это то же самое, но на самом деле в отличие от sample, метод run возвращает результат в несколько ином виде; а еще он позволяет запускать программу на реальном квантовом компьютере Goolge или их новых квантовых симуляторах на TPU:

print(sim.run(circuit, repetitions=25))

(0, 0)=1000010010001110000000010

Тут мы просто видим последовательность наших измерений.

Квантовое машинное обучение#

Импорты#

Мы будем использовать Tensorflow и Tensorflow Quantum.

import os
os.environ["TF_CPP_MIN_LOG_LEVEL"] = "3"
import tensorflow as tf
import tensorflow_quantum as tfq

Задача#

Давайте попробуем решить игрушечную задачку классификации простой гибридной квантово-классической нейронной сетью. У нас будет один квантовый слой и один классический слой. В качестве задачи сгенерируем простенький набор данных, используя рутины scikit-learn. Сразу переведем входящие признаки в диапазон от нуля до \(\pi\).

from sklearn.datasets import make_classification
import numpy as np

x, y = make_classification(n_samples=50, n_features=2, n_informative=2, random_state=42, n_redundant=0)

def normalize(x):
    x_min = x.min()
    x_max = x.max()

    return np.pi * (x - x_min) / (x_max - x_min)

x[:, 0] = normalize(x[:, 0])
x[:, 1] = normalize(x[:, 1])

Посмотрим на эти данные:

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 4))
cb = plt.scatter(x[:, 0], x[:, 1], c=y)
plt.colorbar(cb)
plt.show()

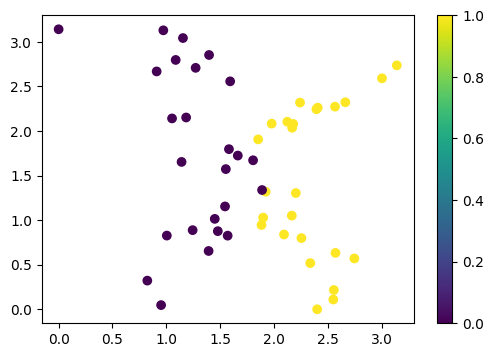
Кубиты#

Tensorflow Quantum позволяет “превращать” параметризированные схемы Cirq в слои нейронных сетей Tensorflow. Но для начала нам все равно потребуется схема. Давайте объявим пару кубитов.

qubits = [cirq.GridQubit(0, 0), cirq.GridQubit(0, 1)]
print(qubits)

[cirq.GridQubit(0, 0), cirq.GridQubit(0, 1)]

Входной слой нейронной сети#

Определим входной слой, который будет кодировать наши классические данные в квантовые. Сразу закодируем данные. Так как Tensorflow работает с тензорами, то нам необходимо будет преобразовать схемы в тензор. Для этого есть специальная функция convert_to_tensor.

def data2circuit(x):
    input_circuit = cirq.Circuit()

    input_circuit.append(cirq.Ry(rads=x[0]).on(qubits[0]))
    input_circuit.append(cirq.Ry(rads=x[1]).on(qubits[1]))

    return input_circuit

x_input = tfq.convert_to_tensor([data2circuit(xi) for xi in x])

Слой из параметризованной схемы#

Для создания параметризованных схем в Tensorflow Quantum используются символы из библиотеки символьных вычислений sympy. Давайте объявим несколько параметров и создадим схему:

from sympy import symbols

params = symbols("w1, w2, w3, w4")

trainable_circuit = cirq.Circuit()

trainable_circuit.append(cirq.H.on(qubits[0]))
trainable_circuit.append(cirq.H.on(qubits[1]))
trainable_circuit.append(cirq.Ry(rads=params[0]).on(qubits[0]))
trainable_circuit.append(cirq.Ry(rads=params[1]).on(qubits[1]))

trainable_circuit.append(cirq.CNOT.on(qubits[0], qubits[1]))

trainable_circuit.append(cirq.H.on(qubits[0]))
trainable_circuit.append(cirq.H.on(qubits[1]))
trainable_circuit.append(cirq.Rx(rads=params[2]).on(qubits[0]))
trainable_circuit.append(cirq.Rx(rads=params[3]).on(qubits[1]))

trainable_circuit.append(cirq.CNOT.on(qubits[0], qubits[1]))

print(trainable_circuit)

(0, 0): ───H───Ry(w1)───@───H───Rx(w3)───@───
                        │                │
(0, 1): ───H───Ry(w2)───X───H───Rx(w4)───X───

Наблюдаемые#

В качестве операторов, которые мы будем измерять, воспользуемся парой \(\hat{XY}\) и \(\hat{YX}\) для наших кубитов:

ops = [cirq.X.on(qubits[0]) * cirq.Y.on(qubits[1]), cirq.Y.on(qubits[0]) * cirq.X.on(qubits[1])]

Гибридная нейронная сеть#

Теперь воспользуемся классическим Tensorflow, чтобы объявить и скомпилировать нашу нейронную сеть, предварительно добавив в нее один классический слой.

зафиксируем случайный генератор

tf.random.set_seed(42)

входной тензор – это в нашем случае тензор типа string, так как это квантовые схемы

cirq_inputs = tf.keras.Input(shape=(), dtype=tf.dtypes.string)

квантовый слой

quantum_layer = tfq.layers.PQC(trainable_circuit, ops)(cirq_inputs)

классический слой и выходной слой

dense_layer = tf.keras.layers.Dense(2, activation="relu")(quantum_layer)
output_layer = tf.keras.layers.Dense(1, activation="sigmoid")(dense_layer)

компилируем модель и смотрим, что получилось. И сразу указываем метрики, которые хотим отслеживать

model = tf.keras.Model(inputs=cirq_inputs, outputs=output_layer)
model.compile(
    optimizer=tf.keras.optimizers.SGD(learning_rate=0.1),
    loss=tf.keras.losses.BinaryCrossentropy(),
    metrics=[
        tf.keras.metrics.BinaryAccuracy(),
        tf.keras.metrics.BinaryCrossentropy(),
    ]
)
model.summary()

Model: "model"

_________________________________________________________________

 Layer (type)                Output Shape              Param #

=================================================================

 input_1 (InputLayer)        [(None,)]                 0

 pqc (PQC)                   (None, 2)                 4

 dense (Dense)               (None, 2)                 6

 dense_1 (Dense)             (None, 1)                 3

=================================================================

Total params: 13

Trainable params: 13

Non-trainable params: 0

_________________________________________________________________

Предсказания со случайной инициализацией#

Наша нейросеть имеет случайные начальные параметры. Давайте посмотрим, что она предсказывает до обучения:

preds = model(x_input).numpy()

plt.figure(figsize=(6, 4))
cb = plt.scatter(x[:, 0], x[:, 1], c=preds)
plt.colorbar(cb)
plt.show()

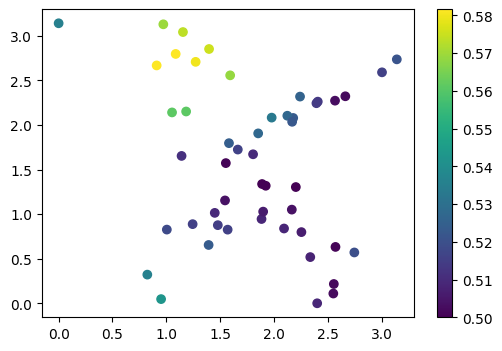
Обучение сети#

запустим обучение

%%time
model.fit(x=x_input, y=y, epochs=200, verbose=0)

CPU times: user 6.04 s, sys: 91 ms, total: 6.13 s
Wall time: 5.58 s

<keras.callbacks.History at 0x7feb44dbd3d0>

визуализируем логи обучения

f, ax = plt.subplots(2, figsize=(6, 6))
ax[0].plot(model.history.history["binary_accuracy"])
ax[1].plot(model.history.history["binary_crossentropy"])
plt.show()

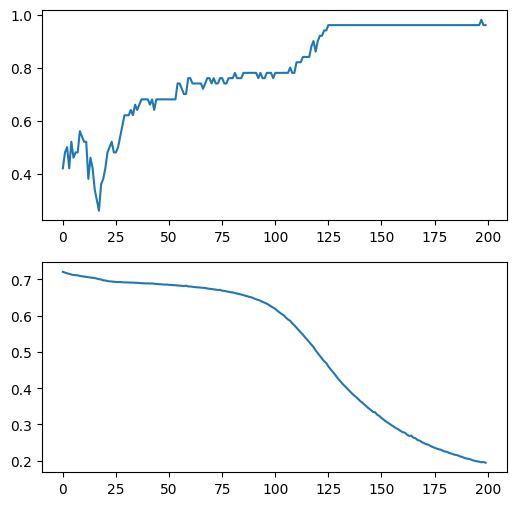
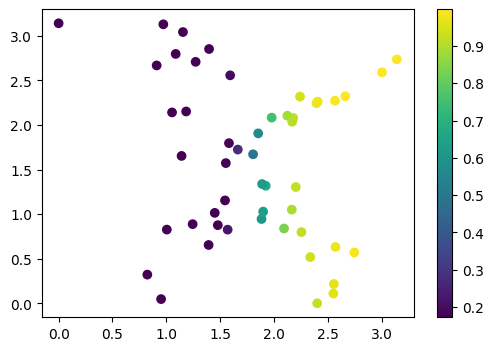
визуализируем предсказания

preds_after_training = model(x_input).numpy()
plt.figure(figsize=(6, 4))

cb = plt.scatter(x[:, 0], x[:, 1], c=preds_after_training)
plt.colorbar(cb)
plt.show()

Заключение#

В данной лекции мы познакомились с фреймворком Tensorflow Quantum. Это достаточно мощный инструмент, особенно в связке с Tensorflow, так как позволяет использовать большое число готовых методов Tensorflow и различных расширений. Тем не менее, для целей обучения Tensorflow Quantum кажется не лучшим выбором, так как имеет много неочевидного синтаксиса и предполагает, как минимум, среднего знания Tensorflow. Во всех дальнейших лекциях мы будем использовать в основном библиотеку PennyLane.

QMLCourse

Cirq & TFQ

Contents

Cirq & TFQ#

Введение#

Работа с кубитами#

Импорты и схема#

Запуск и симуляция#

Квантовое машинное обучение#

Импорты#

Задача#

Кубиты#

Входной слой нейронной сети#

Слой из параметризованной схемы#

Наблюдаемые#

Гибридная нейронная сеть#

Предсказания со случайной инициализацией#

Обучение сети#

Заключение#