Квантовая химия. Введение.

Автор(ы):

• Зимка Борис

Описание лекции

Из этой лекции узнаем:

• что такое квантовая химия, что с ее помощью можно сделать, а что – нельзя;

• как устроена самая простая теория, описывающая квантовую физику атома;

• какие у этой теории есть ограничения.

Введение

В предыдущих лекциях говорили о применении квантовой механики для вычислений и обработки информации. Однако, исторически квантовая теория развивалась в первую очередь из-за того, что классическая физика не могла объяснить некоторые наблюдаемые эффекты: дискретный спектр излучения атомов, фотоэффект в металлах, интерференцию частиц на дифракционных щелях.

Считается, что квантовая механика дает полное и точное описание состояния и эволюции любой системы при нерелятивистских условиях – по крайней мере, на сегодняшний день этому нет экспериментальных или теоретических противоречий. Это значит, что в теории возможно для любой системы частиц записать уравнения Шредингера, решить их и предсказать, как себя поведет система. Между тем, на практике оказывается, что в реальных задачах вроде моделирования лекарств и материалов, просто “взять и посчитать” – задача весьма сложная, а иногда – неразрешимая.

Проблемами применения квантовой механики к химии и материаловедению занимается квантовая химия. Она делает это уже около 100 лет, по теме написаны толстые книжки с многоэтажными формулами, так что в лекции будут даны основы и простые примеры без полного вывода.

Предполагается, что читатель знаком с уравнением Шредингера и основными операторами (импульса, эволюции), бра-кет нотацией, а также помнит основы физики и химии на уровне старших классов школы.

Атом водорода

В чем проблема?

Спектр излучения и поглощения атомов – то есть на какой длине волны происходит поглощение и излучение света веществом – был одной из первых “нерешаемых” проблем, приведших в итоге к появлению квантовой физики. Для простых веществ в газообразной форме спектр является дискретным, и для атома водорода спектры поглощения и излучения в видимом диапазоне выглядят так:

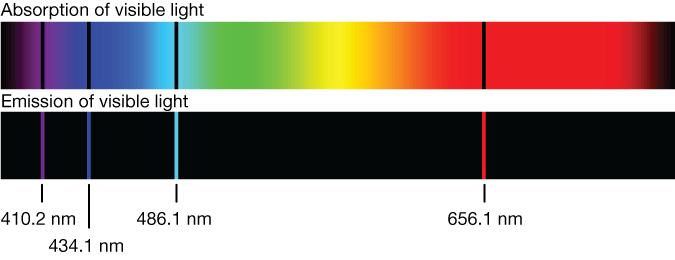
Fig. 84 Спектр поглощения и излучения водорода в видимом диапазоне

В конце 19 века было уже известно, что атом водорода состоит из двух заряженных частиц – протона и электрона, но из классической физики следовало, что спектр излучения такой системы должен быть непрерывным, что никак не стыковалось с наблюдениями (дискретные линии на графике). Попробуем вслед за исследователями квантовой физики начала 20 века разобраться с этой проблемой.

Про имена

“Квантовая физика” и “квантовая механика” – связанные понятия, но не тождественные.

Квантовая механика – это теория (а точнее, множество теорий с различающимися терминологиями), в основе которой лежит аксиоматика о том, что сущности описываются волновыми функциями, что они эволюционируют и, что зная эти функции, можно посчитать физические величины – например, энергию.

Квантовая физика – это область физики, исследующая квантовые эффекты, при этом она местами может не иметь строгого обоснования – лишь бы предсказания работали.

С квантовой химией тоже есть некоторая путаница – в двадцатом веке под ней имели в виду аналитические и численные методы решения задач квантовой механики применительно к молекулам и кристаллам. Но с развитием квантовых компьютеров эту область стали иногда называть вычислительной химией, а квантовой химией – применение квантовых компьютеров к этой области.

Быстрое и неправильное решение

Первой теорией в квантовой физике была “Боровская теория” – почти классическая теория, основанная на постулатах, разрешающих противоречия классической физики с экспериментами на уровне “хардкода”. Главный постулат заключается в том, что момент импульса может принимать только определенные дискретные значения (кванты), а не произвольные:

$$p\cdot r=n\cdot \hslash ,$$

и отсюда

$$p=\frac{n\cdot \hslash }{r},$$

где $p=mv$ – импульс электрона, $r$ – радиус орбиты электрона, $\hslash$ – постоянная Планка, $n$ – любое целое число. Если применить этот постулат к атому водорода – паре из протона и электрона, то получится, что:

• электрон вокруг протона “летает по орбите”;

• спектр (уровни энергии электрона) – дискретный.

Можно показать это следующим образом.

Во-первых, поскольку частиц две и протон имеет массу много больше массы электрона, можно перейти в почти инерциальную систему отсчета протона, где он неподвижен, и решить задачу только для электрона.

Из классической механики берем теорему о вириале (“для стабильной системы из двух частиц, связанных потенциальными силами, в среднем кинетическая энергия равна половине потенциальной”):

$$\begin{array}{r}{E}_k=-E_p/2\\ E=E_k+E_p=E_p/2\end{array}$$

Записываем кинетическую энергию и потенциал Кулона для электрона в поле протона (в СИ):

$$\frac{p^2}{2m}=k\frac{e^2}{2R},$$

где $k$ – постоянная из закона Кулона.

Используем постулат Бора и выразим “радиус” орбиты:

$$\begin{array}{r}\frac{n^2{\hslash }^2}{2m{R}^2}=k\frac{e^2}{2R}\\ R=\frac{n^2{\hslash }^2}{km{e}^2}\end{array}$$

Находим полную энергию:

(19)$$E=E_p/2=-\frac{k{e}^2}{2R}=-\frac{k^2}{n^2}\frac{m{e}^4}{2{\hslash }^2}$$

Уровни энергии пропорциональны $\frac{1}{n^2}$ и именно такая зависимость наблюдается в эксперименте.

Посчитаем минимальную энергию ($n=1$):

from scipy import constants as consts

# постоянная кулона
k = (1 / (4 * consts.pi * consts.epsilon_0))

# энергия в Джоулях
E1 = - k**2 * consts.m_e * consts.e**4 / (2 * consts.hbar ** 2)

# энергия в электрон-вольтах
E1_ev = E1 / consts.e

print(f"Hydrogen Bohr ground state energy: {E1_ev} eV")

Hydrogen Bohr ground state energy: -13.605693122885837 eV

Получившийся ответ (13.6 eV) в точности совпадает с экспериментальным значением энергии ионизации водорода.

Итого: постулировав несколько очень удачных гипотез (главная – что момент импульса квантуется, то есть принимает только дискретные значения), удалось разрешить фундаментальную нестыковку между классической теорией и экспериментом: энергия стала дискретной, линии спектра (длины волн) стали обратно пропорциональны $(\frac{1}{n_{final}^2}-\frac{1}{n_{initial}^2})$, значения энергии ионизации совпадают с реальными измерениями.

Казалось бы, замечательно, проблема решена! Однако теория Бора имеет ряд проблем. Главная из них заключается в том, что теория работает только для “водородоподобных” атомов, то есть состоящих из ядра и одного электрона на внешней оболочке. Уже для атома гелия спектр не согласуется с боровской теорией.

Кроме того, с точки зрения науки, теория Бора – это в некоторым смысле “читерство”. Выбрав удачные постулаты и подставив соответствующие формулы в законы классической физики, получили правильный результат. Но будь постулаты другими, результат получился бы тоже другой, так что фактически постулаты Бора – это гениальная догадка, позволившая угадать правильные результаты для некоторых систем.