Проблема собственных значений#

Автор(ы):

Введение#

Мы с вами узнали, что задачи комбинаторной оптимизации и квантовой химии могут быть сведены к решению проблемы поиска минимального собственного значения большого эрмитова оператора – гамильтониана. Для оптимизационных задач это осуществляется при помощи сведения к QUBO-матрице и гамильтониану типа Изинга. А для электронных орбиталей из квантовой химии можно применить преобразование Жордана-Вигнера и также перейти к спиновому гамильтониану.

Теперь перед нами встает вопрос, а как же искать основное состояние этого гамильтониана? В этой лекции рассмотрим классические методы решения этой проблемы, то есть без квантовых компьютеров. Рассмотрение этих методов и их недостатков покажет то, зачем тут так нужен будет квантовый компьютер.

О проблеме (повторение)#

Эта тема обсуждалась во вводных лекциях по линейной алгебре, в части про собственные вектора и собственные значения.

Итак, пусть у имеется диагонализируемая матрица \(A\) размерности \(n \times n\), она же является линейным оператором \(\hat{A}\). Из линейной алгебры знаем, что у этой матрицы есть \(n\) таких чисел \(e_i\) и векторов \(\Psi_i\), что для них выполняется условие:

\[ A \Psi_i = e_i \Psi_i \]

или в нотации Дирака, которая используется в области квантовых вычислений:

\[ \hat{A} \ket{\Psi_i} = e_i\ket{\Psi_i} \]

Таким образом, собственные вектора – это такие вектора, которые при применении оператора не меняют свое направление. Например, в примере ниже собственный вектор – это ось симметрии оператора:

../../../_images/Mona_Lisa.png

Fig. 98 Синий вектор, в отличии от красного, при применении оператора не меняет направление так как является его собственным вектором.#

Итеративные алгоритмы#

В целом, задача нахождения собственных значений является очень трудной с вычислительной точки зрения, особенно для больших матриц. Для матриц размера более, чем \(3 \times 3\) в общем случае не существует алгоритма нахождения собственных значений и собственных векторов. Однако существует несколько итеративных алгоритмов. Рассмотрим лишь два из них, причем без особых деталей, так как эти алгоритмы, а также доказательство их сходимости являются достаточно сложными.

Степенной метод#

Один из самых простых для понимания алгоритмов, который, тем не менее находит интересные применения. Суть его в том, что берем некоторый случайный вектор \(\ket{\Psi}\) и начинаем последовательно действовать на него оператором \(\hat{A}\) (другими словами умножать, на нашу матрицу), при этом нормируя:

\[ \ket{\Psi_{i+1}} = \frac{\hat{A}\ket{\Psi_i}}{||\hat{A}||} \]

И так повторяем до тех пор, пока изменение вектора не будет меньше, чем некоторое заданное маленькое значение \(\epsilon\). Когда достигли этого условия, это значит что нашли первый собственный вектор, который соответствует наибольшему собственному значению. В частном случае интересных нам эрмитовых операторов, можно так же последовательно находить все собственные вектора и собственные значения.

Note

На самом деле, сеть интернета является графом – множеством связанных между собой вершин. А любой граф можно представить в виде большой-большой, но очень разреженной матрицы, каждый элемент которой это 1 если между соответствующими вершинами есть ребро и 0, если нет. Например, элемент \(L_{ij}\) будет 1, если между вершинами \(i\) и \(j\) есть ребро.иВ 1998-м году, Ларри Пейдж и Сергей Брин нашли очень эффективный способ подсчета первого собственного вектора этой матрицы, используя именно модификацию степенного метода. Этот алгоритм получил название PageRank, причем Page это фамилия автора, а не отсылка к веб-страницам, как можно было бы подумать. Этот алгоритм лег в основу поисковика Google, который в дальнейшем вырос в транснациональную корпорацию!

Итерация Арнольди#

Это гораздо более сложный метод, который, однако, является одним из самых эффективных применительно к разреженным матрицам [Arn51]. Объяснить его легко, к сожалению, не получится, так как алгоритм требует понимания Крыловских подпространств и других концептов из области линейной алгебры разреженных систем. Но пока достаточно лишь того, что этот алгоритм имеет очень эффективную реализацию – ARPACK, написанную в середине 90-х годов на языке FORTRAN77. Именно эта библиотека используется “под капотом” у SciPy, а также во многих других научных пакетах. Давайте посмотрим, как она работает.

Сгенерируем большую разреженную матрицу.

import numpy as np
from scipy import sparse

np.random.seed(42)
x = np.random.random(10000)
np.random.seed(42)
y = np.random.random(10000)
px = np.where(x > 0.2)
py = np.where(y > 0.2)
num_elements = max([px[0].shape[0], py[0].shape[0]])
spmat = sparse.coo_matrix(
    (
        (np.ones(num_elements),
        (px[0][:num_elements], py[0][:num_elements]))
    )
)

print(spmat.__repr__())

<10000x10000 sparse matrix of type '<class 'numpy.float64'>'
	with 7957 stored elements in COOrdinate format>

Матрица размера \(10000 \times 10000\) это большая матрица и работать с ней в “плотном” (dense) представлении было бы очень трудно. Но ARPACK позволяет найти минимальное собственное значение за доли секунд, используя разреженность матрицы:

from scipy.sparse import linalg as sl

max_eigval = sl.eigs(spmat, k=1, which="LR", return_eigenvectors=False)[0]
min_eigval = sl.eigs(spmat, k=1, which="SR", return_eigenvectors=False)[0]

print(f"Min E: {min_eigval}\nMax E: {max_eigval}")

Min E: (-1.1102230246251565e-16+0j)
Max E: (1.0000000000000007+0j)

Для тех кто забыл, какие параметры принимает функция eigs из scipy.linalg.spare напомним, что первый параметр это разреженная матрица, k – сколько именно собственных значений хотим получить, which указывает на собственные значения:

  • SM – smallest magnitude – наименьшие по модулю числа

  • LM – largest magnitude – наибольшие по модулю числа

  • SR – smallers real – числа с наименьшей действительной частью

  • LR – largest real – числа с наибольшей действительной частью

  • SI – smallest image – числа с наименьшей мнимой частью

  • LI – largest image – числа с наибольшей мнимой частью

Наконец, параметр return_eigenvectors – хотим ли получить только собственные значения, или еще и собственные вектора.

Более подробна работа с scipy.sparse, а также с scipy.sparse.linalg разбирается в [вводном блоке по линейной алгебре](пока пусто).

Note

Не у всех матриц все собственные значения являются действительными, поэтому ARPACK по умолчанию считает комплексные значения, хотя в этом конкретном случае видим, что мнимая часть равна нулю.

Алгоритм Ланкзоша#

Итерация Ланкзоша (англ. Lanzos) [Lan50] – это модификация итерации Арнольди, которая работает с эрмитовыми матрицами и находит максимально широкое применение в том числе для квантовых гамильтонианов. Этот алгоритм по умолчанию включен в большинство математических пакетов, включая ARPACK и, соответственно, SciPy:

max_eigval = sl.eigsh(spmat, k=1, which="LM", return_eigenvectors=False)[0]
min_eigval = sl.eigsh(spmat, k=1, which="SM", return_eigenvectors=False)[0]

print(f"Min E: {min_eigval}\nMax E: {max_eigval}")

Min E: -8.323011768995762e-25
Max E: 1.0000000000000002

У этой процедуры из ARPACK немного другие варианты параметра which, так как мы помним, что у эрмитовых матриц собственные значения вещественны:

  • LM – largest magnitude – наибольшие по модулю

  • SM – smallest magnitude – наименьшие по модулю

  • LA – largest algebraic – алгебраически наибольшие, т.е. с учетом знака

  • SA – smallest algebraic – алгебраически наименьшие, т.е. с учетом знака

Вариационные алгоритмы#

В этом разделе поговорим о существующих алгоритмах решения задачи об основном состоянии уже в контексте квантовой механики. Хотя, как помним, задачи оптимизации и квантовой физики тесно связаны. В каком-то смысле, вариационные алгоритмы, а в особенности, квантовый Монте-Карло и различные его модификации в чем-то сильно похожи на классический алгоритм имитации отжига.

Вариационный Монте-Карло#

Variational Monte-Carlo, или просто VMC это очень простой и в тоже время эффективный алгоритм нахождения основного состояния квантомеханической системы.

Note

Замечание – в классическом VMC обычно работают при нулевой температуре. Хотя в общем случае, температура оказывает значительное влияние на то, в каком состоянии находится физическая система.

Давайте еще раз запишем ожидаемое значение энергии гамильтониана в состоянии \(\ket{\Psi}\):

\[ E = \frac{\braket{\Psi | \hat{H} | \Psi}}{\braket{\Psi | \Psi}} \]

Если ввести вектор \(X\), который описывает конфигурацию системы (например, ориентации спинов), то выражение для энергии можно переписать в интегральной форме:

\[ E = \frac{\int |\Psi(X)|^2 \frac{\hat{H}\Psi(X)}{\Psi(X)} dX}{\int |\Psi(X)|^2 dX} \]

В данном случае, выражение

\[ \frac{|\Psi(X)|^2}{\int |\Psi(X)|^2 dX} \]

дает распределение вероятностей, а значит можно из него семплировать, используя методы Монте-Карло. Это очень похоже на то, как ранее семплировали из распределения Больцмана в классическом методе Монте-Карло. Вопрос лишь в том, как представить волновую функцию \(\ket{\Psi}\)? В этом помогут так называемые trial wave functions – параметризированные функции от \(X\). В этом случае меняем или варьируем параметры trial wave function в процессе:

  • семплируем из \(\frac{|\Psi(X)|^2}{\int |\Psi(X)|^2 dX}\) конфигурации;

  • обновляем параметризацию trial function так, чтобы минимизировать энергию.

Повторяем до сходимости. Ну а дальше посмотрим на некоторые примеры trial wave functions.

Jastrow Function#

Когда есть задача из \(N\) квантовых частиц, каждая из которых описывается координатой или радиус вектором, то можно построить trial wave function в виде суммы попарных функций двухчастичных взаимодействий:

\[ \Psi(X) = e^{-\sum_{i,j} u(r_i, r_j)}, \]

где \(r_i, r_j\) – это радиус-векторы частиц, а \(u(r_i, r_j)\) – симметричная функция, описывающая двухчастичное взаимодействия. Такая функция называется Jastrow function [Jas55]. В этом случае, в процессе работы VMC будем просто варьировать радиус-векторы частиц также, как варьировали вершины графа в обычном отжиге, когда решали задачу комбинаторной оптимизации. Только теперь есть еще и параметризация обменных взаимодействий, которую “варьируем”.

Hartree-Fock (SCF)#

Для задач квантовой химии, когда работаем с фермионами, существует вид trial wave function на основе Слэтеровского детерминанта, о котором писали в продвинутой лекции по квантовой химии:

\[ \Psi(R) = D^{\uparrow}D^{\downarrow}, \]

где \(D\) это матрица из одноэлектронных орбиталей:

\[\begin{split} D = \begin{bmatrix} \psi_1(r_1) & \psi_1(r_2) & ... & \psi_1(r_{N / 2}) \\ ... & ... & ... & ... \\ \psi_{N / 2}(r_1) & \psi_{N / 2}(r_2) & ... & \psi_{N / 2}(r_{N / 2}) \\ \end{bmatrix} \end{split}\]

Jastrow Function для спинов#

Дальше нас будут интересовать как раз модели Изинга и спины, а не частицы в пространстве или орбитали из вторичного квантования. Для спинов можем записать Jastrow function следующим образом:

\[ \Psi(s) = e^{\sum_{i,j}s_i W_{i,j} s_j}, \]

где матрица \(W\) будет играть роль параметризации и отражать парные спиновые корреляции. Давайте посмотрим это на практике при помощи библиотеки NetKet [CCH+19].

import netket as nk

Моделировать будем простую модель Изинга для цепочки из 10 спинов (чтобы быстро считалось):

\[ \hat{H} = -h \sum_i \sigma^x_i + J \sum_{i,j}\sigma^z_i \sigma^z_j \]

Параметры возьмем такими:

  • \(J=0.5\)

  • \(h=1.321\)

g = nk.graph.Hypercube(length=10, n_dim=1, pbc=True)
hi = nk.hilbert.Spin(s=0.5, N=g.n_nodes)
op = nk.operator.Ising(h=1.321, hilbert=hi, J=0.5, graph=g)

Поскольку модель относительно небольшая по числу частиц, то сразу можем получить точное решение методом Ланкзоша.

exact = nk.exact.lanczos_ed(op)[0]

Создадим модель на основе Jastrow и VMC:

sampler = nk.sampler.MetropolisLocal(hi)
model = nk.models.Jastrow(dtype=complex)
optimizer = nk.optimizer.Sgd(learning_rate=0.05)
sr = nk.optimizer.SR(diag_shift=0.01)
vmc = nk.driver.VMC(op, optimizer, sampler, model, n_samples=1008, preconditioner=sr)

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/netket/utils/deprecation.py:126: FutureWarning: 

**DEPRECATION_WARNING:**
    The `dtype` argument to neural-network layers and models is deprecated
    throughout NetKet to maintain consistency with new releases of flax.
    Please use `param_dtype` instead.

    This warning will become an error in a future version of NetKet.


  warn_deprecation(_dep_msg)
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

Note

Изучение документации библиотеки NetKet оставляем вам самим, так как объяснение абстракций графа и гильбертова пространства, а также использование метода stochastic reconfiguration для вычисления градиентов выходит за рамки лекции. Документаци представлена на сайте NetKet.

Запустим оптимизацию:

logger = nk.logging.RuntimeLog()
vmc.run(50, out=logger, show_progress=False)

(RuntimeLog():
  keys = ['Energy'],)

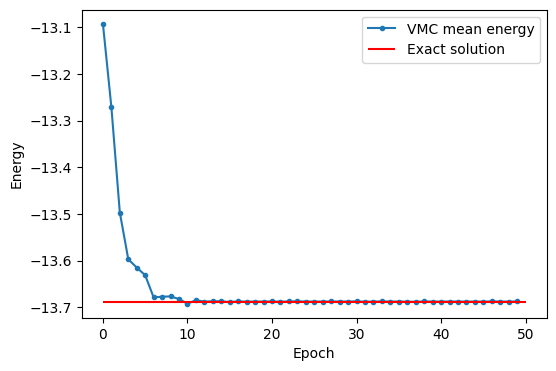
Посмотрим на результат:

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 4))
plt.plot(list(range(50)), np.real(logger.data["Energy"]["Mean"]), ".-", label="VMC mean energy")
plt.xlabel("Epoch")
plt.ylabel("Energy")
plt.hlines(exact, 0, 50, label="Exact solution", color="red")
plt.legend()
plt.show()
../../../_images/eigenvals_17_0.png

Neural Network Quantum States#

Еще более интересный подход к выбору trial wave function – это использование в качестве \(\Psi(X)\) нейронной сети [CT17]. Уже немного касались этой темы, когда речь шла о видах квантового машинного обучения. Хороший вариант, это использовать, например, полносвязную сеть – ограниченную машину Больцмана:

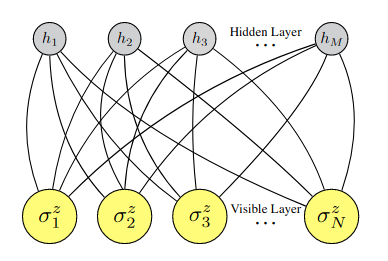
../../../_images/NQS.png

Fig. 99 Нейронная сеть в качестве trial wave function из работы [CT17].#

Это также легко может быть реализовано с использованием библиотеки NetKet:

model = nk.models.RBM()
optimizer = nk.optimizer.Sgd(learning_rate=0.05)
sr = nk.optimizer.SR(diag_shift=0.01)
vmc = nk.driver.VMC(op, optimizer, sampler, model, n_samples=1000, preconditioner=sr)

logger = nk.logging.RuntimeLog()
vmc.run(50, out=logger, show_progress=False)

plt.figure(figsize=(6, 4))
plt.plot(list(range(50)), np.real(logger.data["Energy"]["Mean"]), ".-", label="VMC mean energy")
plt.xlabel("Epoch")
plt.ylabel("Energy")
plt.hlines(exact, 0, 50, label="Exact solution", color="red")
plt.legend()
plt.show()

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/netket/vqs/mc/mc_state/state.py:58: UserWarning: n_samples=1000 (1000 per MPI rank) does not divide n_chains=16, increased to 1008 (1008 per MPI rank)
  warnings.warn(
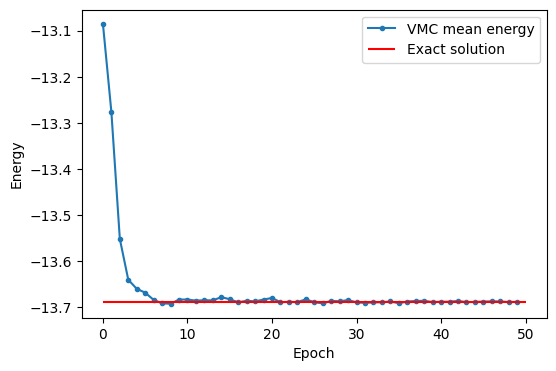
../../../_images/eigenvals_19_1.png

Преимущества использования нейронной сети трудно показать на таком небольшом примере с моделью Изинга и 10-ю спинами, но они полностью раскрываются, если нужно анализировать более сложные модели.

Note

Это интересно, но при помощи библиотеки NetKet можно по сути решать проблемы комбинаторной оптимизации [SB19] с помощью методов deep learning.

Проблемы с VMC#

К сожалению, у метода VMC есть свои проблемы. Это относительно плохая масштабируемость – при росте размерности проблемы для того, чтобы подобрать реально хорошую аппроксимацию потребуется все больше итераций и семплов на каждой из них. Также у VMC есть ряд фундаментальных проблем, например, так называемая sign problem [LJGS+90].

Заключение#

В этой лекции рассмотрены известные подходы к решению задачи о минимальном собственном значении на классическом компьютере. Как увидели, все эти методы не могут быть масштабированы на реально большие операторы. Так что для решения этих проблем действительно нужен квантовый компьютер.