Сверхпроводниковые кубиты

Автор(ы):

• Беседин Илья

Сверхпроводниковые кубиты относятся к наиболее успешным типам кубитов для квантовых вычислений и симуляции на сегодняшний день. Google впервые продемонстрировала квантовое превосходство на квантовом процессоре из 53 сверхпроводниковых кубитов-трансмонов [AAB+19]. Кроме Google, сверхпроводниковые кубиты используют IBM (в том числе для своего открытого облачного проекта IBM Quantum Experience), Riggetti Computing и другие крупные фирмы и лаборатории по всему миру.

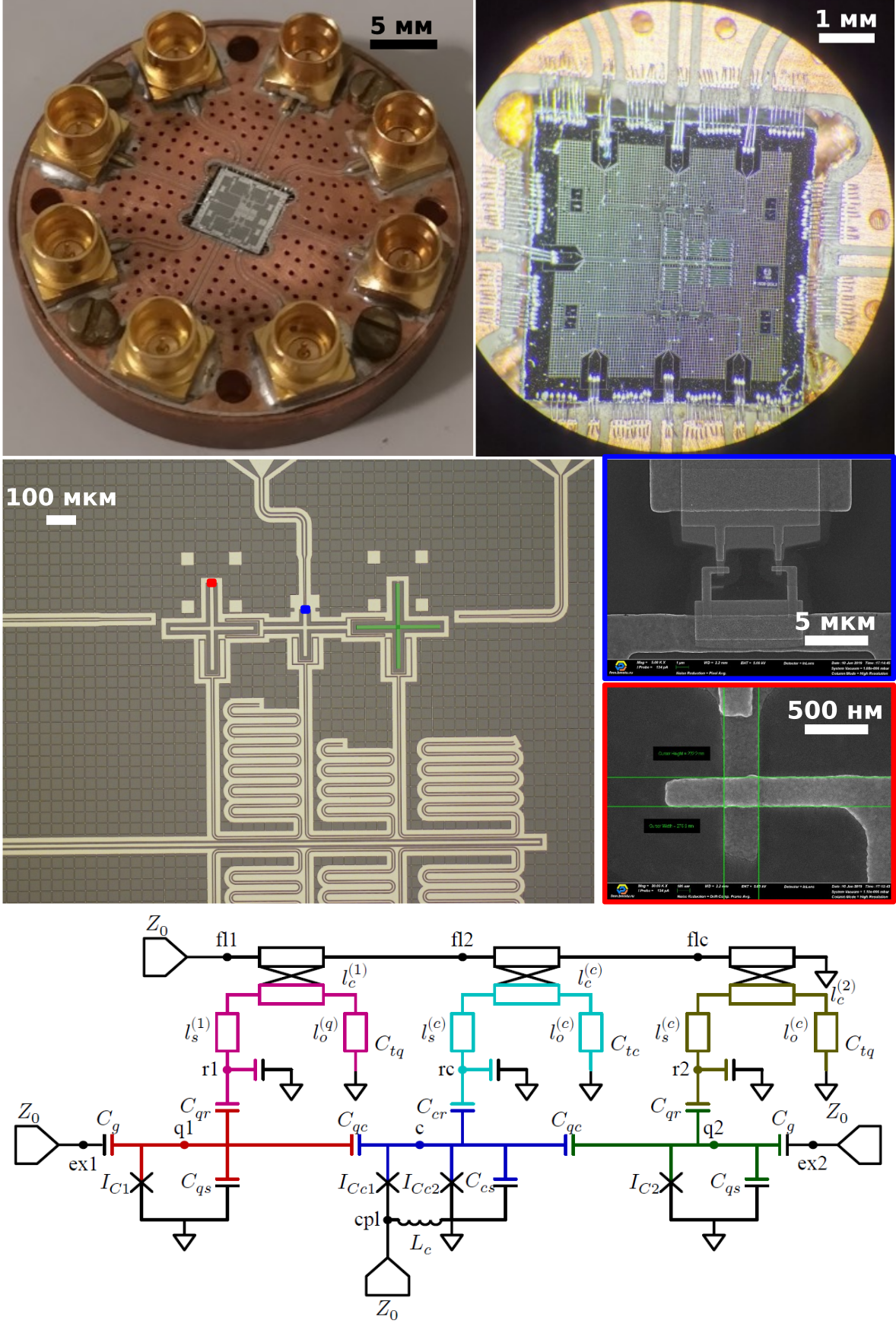
Fig. 45 Фотографии, изображения со сканирующего электронного микроскопа и эквивалентная электрическая схема микросхемы сверхпроводникового квантового процессора с двумя кубитами-трансмонами. Синим отмечен электрод одного из трансмонов. Микросхема была изготовлена в НОЦ ФМН в МГТУ им. Баумана, топология разработана в НИТУ МИСиС.

Квантовый процессор на сверхпроводниковых кубитах – это электрическая цепь. Эту электрическую цепь можно изобразить в схемы с квазисосредоточенными элементами.

Квантование электрических цепей

Электрические цепи, как и любые другие физические объекты, могут быть описаны с помощью законов квантовой механики [VD17]. Для этого следует начать с гамильтонового описания, например с помощью функции Лагранжа. Энергия всей физической системы (электрической цепи) должна быть записана в виде суммы энергий, накопленных ее составными частями (сосредоточенных элементов), выраженной через динамическое переменные системы и их производные. Самые простые электрические элементы, такие как конденсаторы и индукторы, запасают энергию \(E_C\) и \(E_L\) в электрическом и магнитном поле, а выражение для них можно записать либо через заряд на обкладках \(Q\) и поток через кольцо \(\Phi\), либо через напряжение \(V\) и ток \(I\), соответственно:

\[ E_C = \frac{Q^2}{2C}=\frac{CV^2}{2}, \]

\[ E_L = \frac{\Phi^2}{2L}=\frac{LI^2}{2}. \]

Для третьего самого простого линейного элемента электрической цепи, резистора, так сделать не получится. Резистор не накапливает в себе энергию, он ее диссипирует. Диссипативные системы не могут быть описаны исключительно при помощи функции Лагранжа. Это не значит, что резистор совершенно невозможно адекватно описать в гамильтоновом формализме: он может быть представлен как бесконечный резервуар энергии, так как с точки зрения остальной цепи не слишком важно, осталась ли энергия в резисторе или она была рассеяна, если она никогда больше не вернется в остальные элементы цепи. Резисторы не слишком полезны в квантовой обработке информации, так как любые потери энергии приводят к неунитарной эволюции, потере когерентности и в конечном счете – ошибкам вентилей.

В электротехнике, как правило, используются переменные \(V\) и \(I\): напряжение и ток можно померить, правильно подключив измерительные приборы к проводникам цепи, в то время как измерения \(Q\) и \(\Phi\) затруднены, так как заряды и потоки локализованы внутри элементов. Но \(V\) и \(I\) не подходят в качестве переменных, от которых зависит функция Лагранжа, так как ни одна из них не является производной другой. Зато из закона сохранения заряда следует, что \(\dot{Q}=-I\), а закон индукции Фарадея говорит, что \(\dot{\Phi}=V\), а значит и \(\Phi\), и \(Q\) могут быть использованы в качестве динамических переменных системы.

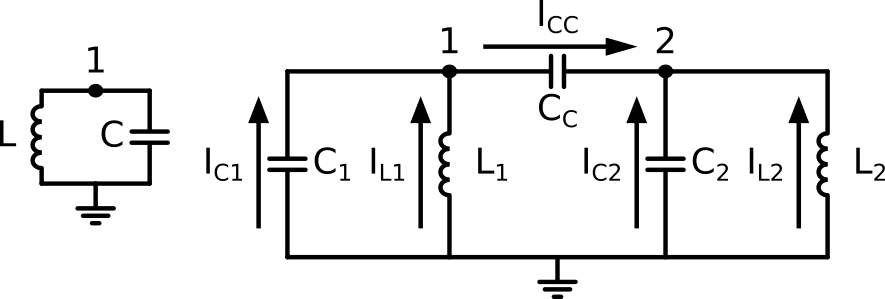
Fig. 46 Электрические схемы одного LC-контура и двух емкостно связанных LC-контуров.

В случае одной степени свободы определения для величин \(Q\), \(\Phi\), \(V\) и \(I\) однозначны. В более сложных случаях в классической электротехнике принято использовать метод контурных токов, либо узловых напряжений. Рассмотрим метод узловых напряжений. Для лагранжевого описания введем узловой поток \(\Phi_i(t)\) как первообразную напряжения на узле с номером \(i\) \(V_i(t)\):

\[ \Phi_i(t) = \int\limits_0^t V_i(t) \mathrm{d}t. \]

Функция Лагранжа LC-контура имеет вид

\[ L(\Phi_1, \dot{\Phi}_1) = \frac{C\dot{\Phi}_1^2}{2}-\frac{\Phi_1^2}{2L}. \]

Канонически сопряженный импульс \(Q_i\) к обобщенной переменной \(\Phi_i\) можно найти по формуле

\[ Q_i = \frac{\partial L}{\partial \dot{\Phi}_i} = C\dot{\Phi}_i. \]

Физический смысл этого импульса – сумма зарядов на конденсаторах, примыкающих к узлу \(i\), или узловой заряд.

Функция Гамильтона \(H(\Phi_i, Q_i)\) представляет собой преобразование Лежандра от функции Лагранжа по парам \((\dot{\Phi}_i, Q_i)\), то есть

\[ H(\Phi_i, Q_i) = \dot{\Phi}_i \dot{Q}_i - L = \frac{Q_i^2}{2C} + \frac{\Phi_i^2}{2L}. \]

Оператор Гамильтона может быть получен из функции Гамильтона заменой переменных \(\Phi_1, Q_1\) на соответствующие операторы:

\[ H = \frac{\hat{Q}_1^2}{2C} + \frac{\hat{\Phi}_1^2}{2L}. \]

Здесь \([\hat{Q}_1, \hat{\Phi}_1]=-i\hbar\) в силу того, что \(\Phi_1\) и \(Q_1\) – каноническая переменная и сопряженный к ней импульс. Волновая функция системы может быть записана в потоковом \(\psi_\Phi(\Phi_1)\) или зарядовом \(\psi_Q(Q_1)\) представлении. Переход от одного представления к другому, как в случае обыкновенных координат и импульсов, может быть произведен с помощью преобразования Фурье

\[ \psi_\Phi(\Phi_1)=\frac{1}{\sqrt{2\pi}}\int e^{i\Phi_1 Q_1}\psi_Q(Q_1, Q_2)\mathrm{d}Q_1. \]

Как и в случае механических осцилляторов, для LC-осцилляторов очень полезен формализм операторов вторичного квантования \(\hat{a}\) и \(\hat{a}^\dagger\), которые можно определить как

\[ \hat{Q}_1 = \sqrt{\frac{\hbar}{2Z}}(\hat{a}_1+\hat{a}_1^\dagger), \]

\[ \hat{\Phi}_1 = i\sqrt{\frac{\hbar Z}{2}}(\hat{a}_1-\hat{a}_1^\dagger), \]

где \(Z=\sqrt{L_1/C_1}\) – импеданс осциллятора. В этом формализме гамильтониан системы принимает вид

\[ \hat{H} = \hbar\omega_1(\hat{a}_1^\dagger\hat{a}_1+\frac{1}{2}), \]

где \(\omega_1=(L_1C_1)^{-1/2}\) – частота осциллятора.

Джозефсоновский контакт

Линейные электрические элементы, такие как емкости и индуктивности, очень полезны при создании электронных приборов. Но из линейных элементов можно создать только линейную электрическую цепь. Это означает, что любые выходные сигналы \(V^\mathrm{out}_i(\omega)\) выражаются через входные сигналы \(V^\mathrm{in}_j(\omega)\) с помощью линейного преобразования

\[ V^\mathrm{out}_i(\omega)=\sum\limits_j S_{ij}(\omega) V^\mathrm{in}_j(\omega). \]

Это выражение остается справедливым и для квантового случая, где величина \(V^\mathrm{out}_i(\omega)\) является оператором. \(S_{ij}(\omega)\) - это передаточная функция, или S-параметр системы. Для линейной системы S-параметр зависит лишь от частоты сигнала, но не зависит от состояния системы. По существу линейные системы не обладают состоянием, т.е. не могут играть роль памяти. В частности, такие системы не могут эффективно симулировать машину Тьюринга и тем более квантовую машину Тьюринга. Они могут реализовывать некоторое линейное преобразование над входными данными, однако это линейное преобразование жестко задано топологией и номиналами емкостей и индуктивностей цепи.

Для того, чтобы создать архитектуру компьютера, в которой есть память или управление, нужны нелинейные элементы. В классической электронике в качестве нелинейного элемента чаще всего используют транзистор. Наиболее популярный в интегральных микросхемах - это полевой транзистор. Полевой транзистор имеет три контакта, причем напряжение между затвором и стоком управляет сопротивлением между стоком и истоком. Для квантовой обработки информации управление сопротивлением – не самый практичный вариант, в связи с тем, что протекание тока через конечные сопротивления приводит к ошибкам квантовых вентилей.

В качестве альтернативы полупроводниковым нелинейным элементам вроде транзистора и диода можно использовать сверхпроводниковые нелинейные элементы. Одним из таких элементов является джозефсоновский контакт сверхпроводник-изолятор-сверхпроводник (Superconductor-insulator-superconductor, SIS).

Для гамильтонового описания джозефсоновского контакта как элемента электрической цепи используется джозефсоновская энергия, которая определяется соотношением

\[ E_J = \frac{I_c \Phi_0}{2\pi}(1-\cos \phi), \]

где \(I_c\) – критический ток контакта, \(\Phi_0 = h/2e\) – квант магнитного потока в сверхпроводнике, \(\phi = 2\pi \Phi/\Phi_0\) – обезразмеренная на квант потока разность узловых потоках на берегах контакта. Эта величина одновременно является фазой конденсата куперовских пар в сверхпроводнике. Для понимания принципов работы сверхпроводниковых кубитов совершенно необязательно понимать физику самой сверхпроводимости, что такое куперовская пара, что подразумевается под словом конденсат и что значит его фаза. С точки зрения схемотехники кубитов, все знания о физике сверхпроводников могут быть сведены к определению фазы и соотношением для энергии контакта в зависимости от фазы. Эти соотношения однозначно определяют поведение потоков и зарядов в цепи. Мы будем пользоваться фазой вместо узлового потока исключительно из-за того, что эта величина является безразмерной, и это позволит упростить все соотношения. Также заряд будет измеряться в единицах заряда куперовской пары, то есть \(2e\).

Дифференцируя соотношение для джозефсоновской энергии по потоку, можно получить выражение для индуктивности джозефсоновского контакта

\[ L_J=\frac{1}{\frac{\partial^2 E}{\partial \Phi^2}} = \frac{2\pi\Phi_0^2}{I_c \Phi_0 (2\pi)^2\cos \phi}=\frac{\Phi_0}{I_c 2\pi \cos \phi}. \]

Трансмон

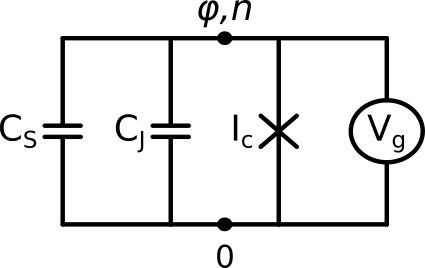
Fig. 47 Электрическая схема трансмона. \(I_c\) – критический ток контакта, \(C_S\) – шунтриующая емкость, \(C_J\) – емкость контакта

Самый простой, и в то же время один самых успешных видов сверхпроводниковых кубитов – это трансмон[KYG+07]. Трансмон представляет собой ангармонический осциллятор на основе наноразмерного джозефсоновского контакта, шунтированного емкостью. Такая цепь хорошо известна в сверхпроводниковой электронике, а ее резонансная частота называется плазменной частотой:

\[ \omega_{\mathrm{p}} = \frac{1}{\sqrt{L_{J}(C_J+C_S)}}. \]

В квантовом случае, свойства этого осциллятора могут зависеть от постоянного напряжения \(V_g\). Наступление квантового режима определяется произведением критического тока и емкости; фактически, в зависимости от этого произведения, такая схема может быть классическим осциллятором, трансмоном или зарядовым кубитом.

Гамильтониан трансмона (а также зарядового кубита) имеет вид

\[ \hat{H} = \frac{(2e)^2(\hat{n}-n_\mathrm{g})^2}{2(C_J+C_S)} + \frac{I_c\Phi_0}{2\pi}(1-\cos\hat{\phi}), \]

где \(\hat{n}=\hat{Q}/2e\), \(\hat{\phi}=\frac{2e}{\hbar}\hat{\Phi}\) – безразмерные операторы числа и фазы куперовских пар на электроде, а \(n_\mathrm{g}\) – средний наведенный на острове внешними источниками напряжения заряд. Гамильтониан можно упростить, заменив произведения размерных константы на параметры

\[ E_C=\frac{e^2}{2(C_J+C_S)} \]

\[ E_J=\frac{I_c\Phi_0}{2\pi}, \]

которые называют емкостной и джозефсоновской энергией трансмона, соответственно. В этих обозначениях гамильтониан принимает вид

\[ \hat{H} = 4E_C(\hat{n}-n_g)^2+E_J(1-\cos\hat{\phi}). \]

Уровни энергии стационарных состояний в такой системе будут зависеть от приложенного напряжения (вернее, от наведенного внешним напряжением \(V_g\) зарядом \(n_g\)). Однако эта зависимость ослабевает по мере того, как увеличивается соотношение \(E_J/E_C\).

Fig. 48 Уровни энергии в зарядовом кубите и в трансмоне

Трансмоном называется режим этой электрической цепи, когда \(E_J/E_C \sim 50\); при таком соотношении между константами зависимость от заряда практически отсутствует. Это очень хорошо, потому что наведенный заряд очень сложно контролировать на практике. Космические частицы и события радиоактивного распада в подложке приводят к запиранию зарядов в случайных местах в подложке, из-за чего зарядово-чувствительные кубиты могут менять частоту перехода между уровнями. Уровни энергии в трансмоне не чувствительны к таким воздействиям, что значительно улучшает их времена когерентности по сравнению с зарядовыми кубитами. Обратной стороной такой схемы является невысокий ангармонизм. Ангармонизмом \(\delta\) называется разность частот между переходами \(|0\rangle \leftrightarrow |1\rangle\) и \(|1\rangle \leftrightarrow |2\rangle\). У трансмона \(\delta = -E_C\). По существу, трансмон является слабо ангармоничным осциллятором. Однако расстояния между частотами переходов в трансмоне достаточно большие, чтобы можно было попасть в один переход и при этом не попасть в соседний.

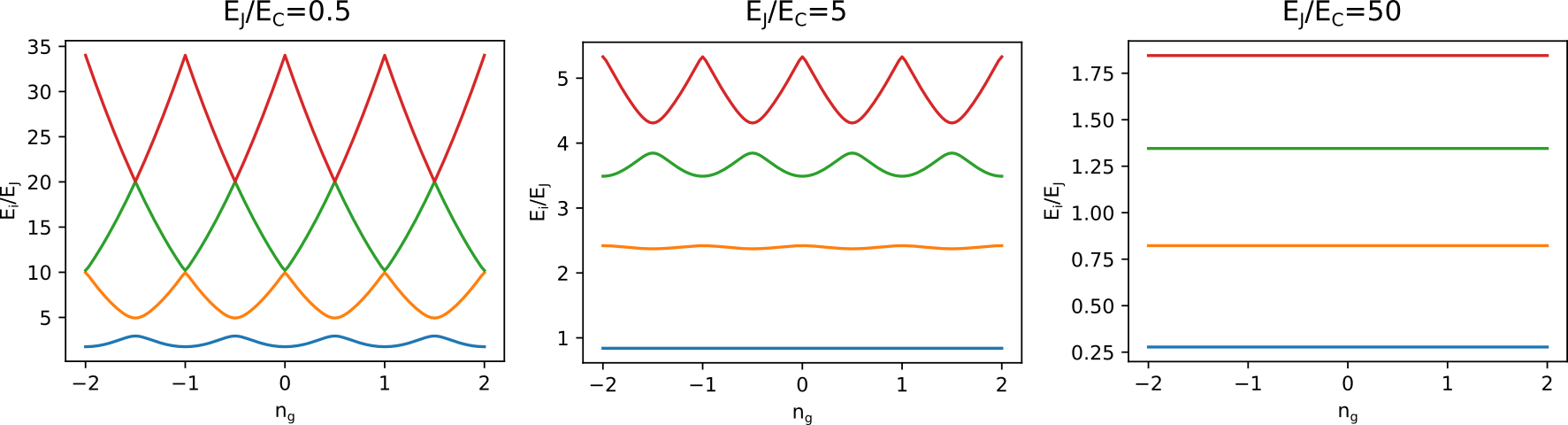
Fig. 49 Уровни энергии и волновые функции стационарных состояний трансмона с \(E_J/E_C=50\)

Считывание

Считывание состояния кубита в сверхпроводящих цепях, как правило, осуществляется методом дисперсионного считывания [WSB+05]. В основе дисперсионного считывания состояния сверхпроводниковых кубитов стоит архитектура квантовой электродинамики в электрической цепи, в которой сверхпроводниковый кубит связан с микроволновым резонатором. Концепция квантовой электродинамики в электрической цепи возникла по аналогии с квантовой электродинамикой в полости, где уединенный атом помещается в оптическую полость, которая выступает в роли резонатора. Взаимодействие такого атома с излучением сильно отличается от того, что происходит с таким атомом, помещенном в вакуум: из-за отражений от стенок полости, излучение не может эффективно покинуть атом. Это увеличивает время жизни атома, если резонансная частота полости находится вдали от спектральной линии кубита. Напротив, если атом находится в резонансе с полостью, то это стимулирует излучение.

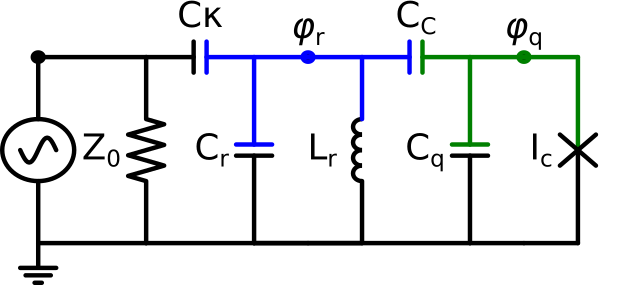
Fig. 50 Эквивалентная электрическая схема трансмона, связанного с резонатором. Синий — электрод резонатора, зеленый — электрод трансмона

Для многокубитных схем, как правило, в качестве микроволнового резонатора используется участок копланарной передающей линии на микросхеме. Микроволновый резонатор, в свою очередь, подключается к микроволновой линии.

Пропускание микроволновых сигналов через линию приводит к изменению квантового состояния электромагнитного излучения в резонаторе; это излучение взаимодействует с кубитом. Преимуществом данной схемы является то, что кубит может быть очень сильно связан с резонатором, но при этом сохраняет когерентность. Если пренебречь влиянием потерь в управляющую линию, то система описывается гамильтонианом вида

\[ \hat{H}/\hbar = \left( \omega_q+\frac{1}{2}\delta_q \left( \hat{a}^\dagger\hat{a}-1 \right) \right)\hat{a}^\dagger\hat{a} + \left( \omega_r+\frac{1}{2}\delta_r \left( \hat{b}^\dagger\hat{b}-1 \right) \right)\hat{b}^\dagger\hat{b} + \chi \left( \hat{a}^\dagger\hat{a}+\frac{1}{2} \right) \left( \hat{b}^\dagger\hat{b}+\frac{1}{2} \right), \]

где \(\omega_q\), \(\omega_r\) – частоты кубита и резонатора, соответственно; \(\delta_r, \delta_q\) – ангармонизмы мод трансмона и резонатора; \(\chi\) – дисперсионный сдвиг, или кросс-керровская нелинейность между трансмоном и резонатором, \(\hat{a}\), \(\hat{a}^\dagger\) – одночастичные операторы уничтожения и рождения, действующие на моду трансмона, \(\hat{b}\), \(\hat{b}^\dagger\) – одночастичные операторы рождения и уничтожения, действующие на моду резонатора, \(\Omega(t)\) – амплитуда возбуждения со стороны микроволновой линии.

Если емкость \(C_C\) между трансмоном и резонатором маленькая, а их частоты сильно отличаются, то взаимодействие между ними будет нерезонансным, и тогда ангармонизмом резонатора можно пренебречь. А вот наличие дисперсионного сдвига между модой кубита и резонатора приводит к тому, что частота эффективная резонатора, то есть сумма всех чисел перед множителем \(\hat{b}^\dagger\hat{b}\), зависит от населенности трансмона. В таком случае, измеряя отклик от резонатора на микроволновый импульс вблизи его резонансной частоты, мы можем получить информацию о состоянии кубита.

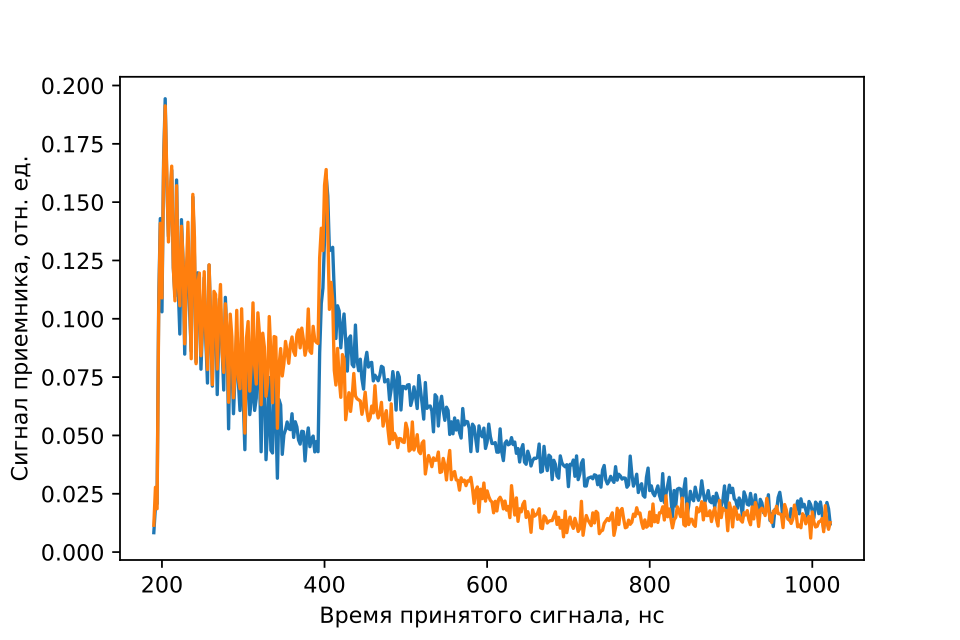
Fig. 51 Микроволновый прямоугольный импульс, отраженный от резонатора, при различных состояниях трансмона. Усреднено по 10000 повторениям.

Микроволновые однокубитные операции

Логические операции над кубитами выполняют микроволновыми сигналами на резонансной частоте кубита. Поведение трансмона по отношению к внешнему излучению можно представить в виде гамильтониана

\[ \hat{V} = V_\mathrm{ex1}(t) \frac{C_g}{C_g+C_{qs}} \hat{Q} \]

для схемы с возбуждением напряжением \(V_\mathrm{ex1}(t)\), подаваемым через маленький конденсатор. Пусть

\[ V_\mathrm{ex1}(t) = V_I(t) \cos \left(\omega_q t + \phi(t) \right) + V_Q(t) \sin \left(\omega_q t + \phi(t) \right), \]

где \(V_I(t), V_Q(t)\) – медленно изменяющиеся огибающие напряжения, а \(\phi(t)\) – медленно изменяющаяся фаза. “Медленно изменяющаяся” здесь означает, что за переходы между уровнями будет отвечать только быстро осциллирующий множитель. Обозначим

\[ \Omega(t) = I(t) - iQ(t) = \frac{C_g}{C_g+C_{qs}}\sqrt{\frac{\hbar}{2Z}}\left(V_I-iV_Q\right). \]

Полный гамильтониан трансмона с возбуждающим излучением будет иметь вид

\[ \hat{H}_\mathrm{dr}/\hbar = \hat{H}/\hbar + \hat{V}/\hbar = \left(\omega_q+\frac{1}{2}\delta_q\left(\hat{a}^\dagger\hat{a}-1\right)\right)\hat{a}^\dagger\hat{a} + \frac{1}{2}\left(\Omega(t)e^{i\left(\omega_q t + \phi(t)\right)} + \Omega^*(t)e^{-i\left(\omega_q t + \phi(t)\right)}\right) \left(\hat{a}+\hat{a}^\dagger\right). \]

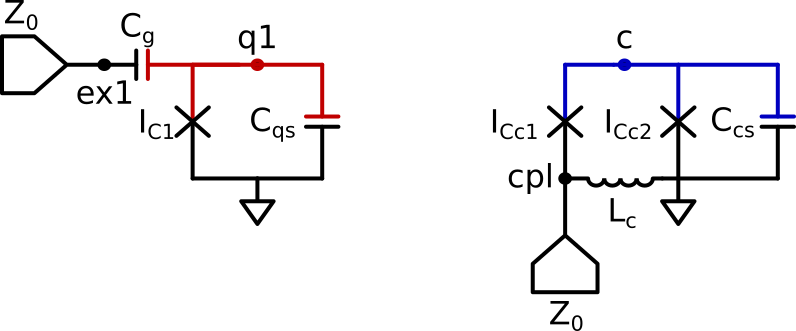
Fig. 52 Трансмон с линиями для микроволновых однокубитных операций. Слева – емкостно связанная линия (через конденсатор), справа – индуктивно связанная линия (через индуктивность).

Если трансмон использовать как кубит (то есть не возбуждать никаких уровней, кроме основного и первого возбужденного), можно перейти от операторов повышения и понижения к операторам Паули с помощью соотношений

\[\begin{split} \hat{a}^\dagger\hat{a} = -\frac{1}{2}\hat{\sigma}_z \\ \hat{a} + \hat{a}^\dagger = \hat{\sigma}_x \\ i\left(\hat{a}-\hat{a}^\dagger\right) = \hat{\sigma_y}. \end{split}\]

Тогда мы получим гамильтониан вида

\[ \hat{H}_\mathrm{dr}/\hbar = \frac{1}{2}\left(\Omega(t)e^{i\left(\omega_q t + \phi(t) \right)} + \Omega^*(t)e^{-i\left(\omega_q t + \phi(t) \right)}\right)\sigma_x. \]

Такое возбуждение отвечает модели Раби для двухуровневой системы. Модель Раби хорошо известна в квантовой оптике, так как она описывает когерентное взаимодействие одного атома с лазерным излучением. Здесь мы остановимся поподробнее, так как модель Раби имеет центральное значение для однокубитных операций на очень широком классе различных кубитов.

Пусть \( |\psi(t)\rangle = \begin{pmatrix} c_0 \\ c_1 \end{pmatrix} \) – решение уравнения Шредингера. Для того, чтобы решить уравнение Шредингера, которое является системой двух обыкновенных линейных дифференциальных уравнений относительно \(c_0(t)\) и \(c_1(t)\), нужно сделать замену

\[\begin{split} c_0(t) = d_0(t)e^{-i\omega_q t/2}, \\ c_1(t) = d_1(t)e^{+i\omega_q t/2}. \end{split}\]

Эта замена называется переходом во вращающуюся систему отсчета. В данном случае, система отсчета вращается вместе с быстро осциллирующей частью микроволнового сигнала. Эта замена может быть записана в виде произведения матрицы на вектор:

\[\begin{split} \begin{pmatrix} c_0(t) \\ c_1(t) \end{pmatrix} = \begin{pmatrix} e^{i\left(\omega_q t + \phi(t)\right)/2} & 0 \\ 0 & e^{-i\left(\omega_q t + \phi(t)\right)/2} \end{pmatrix} \begin{pmatrix} d_0(t) \\ d_1(t) \end{pmatrix}. \end{split}\]

Матрица этого линейного преобразования \(\hat{U} = e^{i\left(\omega_q t + \phi(t)\right)/2 \hat{\sigma}_z}\) является унитарной – ее собственные числа по модулю равны единице. Если подставить эту замену в уравнение Шредингера

\[ i\hbar \partial |\psi \rangle /\partial t = \hat{H}_\mathrm{dr} |\psi \rangle, \]

то получим систему

\[\begin{split} i\dot{d}_0 e^{i\left(\omega_q t + \phi(t)\right)/2} + \frac{\omega_q + \dot{\phi}}{2} d_{0} e^{i\left(\omega_q t + \phi(t)\right)/2} & = & - \frac{\omega_q}{2} d_{0} e^{i\left(\omega_q t + \phi(t)\right)/2} + d_1 e^{i\left(\omega_q t + \phi(t)\right)/2} \left(\Omega(t)e^{i\left(\omega_q t + \phi(t)\right)} + \Omega^*(t)e^{-i\left(\omega_q t + \phi(t)\right)} \right), \\ i\dot{d}_1 e^{-i\left(\omega_q t + \phi(t)\right)/2} - \frac{\omega_q + \dot{\phi}}{2} d_{1} e^{-i\left(\omega_q t + \phi(t)\right)/2} & = & \frac{\omega_q}{2} d_{1} e^{-i\left(\omega_q t + \phi(t)\right)/2} + d_0 e^{i\left(\omega_q t + \phi(t)\right)/2} \left(\Omega(t)e^{i\left(\omega_q t + \phi(t)\right)} + \Omega^*(t)e^{-i\left(\omega_q t + \phi(t)\right)} \right). \end{split}\]

Нехитрыми алгебраическими преобразованиями можно упростить гамильтониан до вида

\[\begin{split} i\dot{d}_0 + \frac{\dot{\phi}(t)}{2}d_0 & = & \left(\Omega(t)e^{i2\left(\omega_d t + \phi(t)\right)} + \Omega^*(t) \right)d_1, \\ i\dot{d}_1 - \frac{\dot{\phi}(t)}{2}d_1 & = & \left(\Omega(t) + \Omega^*(t)e^{-i2\left(\omega_d t + \phi(t)\right)} \right) d_0. \end{split}\]

Далее используют “приближение вращающейся волны”, смысл которого в том, чтобы отбросить быстро осциллирующие слагаемые в гамильтониане с множителями \(e^{-2i\omega_d t}\) и \(e^{2i\omega_d t}\). При не очень больших амплитудах возбуждающих сигналов \(\Omega \ll \omega\), эти слагаемые слишком быстро меняются, чтобы оказать существенное влияние на более медленное изменение \(d_0(t)\) и \(d_1(t)\).

Получается система уравнений уже с постоянными коэффициентами

\[\begin{split} i\dot{d}_0 + \frac{\dot{\phi}(t)}{2}d_0 & = &~\Omega^*(t)d_1, \\ i\dot{d}_1 - \frac{\dot{\phi}(t)}{2}d_1 & = &~\Omega(t)d_0, \end{split}\]

которую можно записать через операторы Паули в виде

\[ i |\tilde{\psi}(t)\rangle = \left( I(t)\hat{\sigma}_x + Q(t)\hat{\sigma}_y - \frac{\dot{\phi}(t)}{2}\hat{\sigma}_z \right)|\tilde{\psi}(t)\rangle, \]

где \(|\tilde{\psi}(t)\rangle = \begin{pmatrix}d_0(t) \\ d_1(t) \end{pmatrix}\).

Такой гамильтониан отвечает вращению вектора состояния кубита в представлении сферы Блоха вокруг оси \(\vec{\Omega} = \{I(t), Q(t), \dot{\phi}(t)/2\}\) с угловой скоростью \(|\vec{\Omega}|\).

Наиболее часто используются микроволновые импульсы, отвечающие вращениям на углы \(\pi/2\) и \(\pi\) вокруг осей \(x\) или \(y\), однако реально любая однокубитная операция может быть реализована правильным подбором управляющих сигналов \(I(t)\), \(Q(t)\), или \(\phi(t)\).

Декогеренция в сверхпроводниковых кубитах

В отличие от других типов кубитов, сверхпроводниковые кубиты имеют сравнительно низкие времена когерентности. Это означает, что информация, хранящаяся в сверхпроводниковом кубите, может испортиться. Для сверхпроводниковых кубитов декогеренцию можно понимать как неконтролируемое воздействие на кубит со стороны флуктуаций напряжения или тока. Природа флуктуаций может быть очень разной. Наиболее проблематичными являются флуктуации микроскопических зарядов и магнитных моментов внутри самой микросхемы.

Как правило различают шумы и наводки, которые могут привести самопроизвольному возбуждению или релаксации кубита, а также к переходу в недопустимые состояния типа уровней \(|2\rangle\) и выше, и шумы, которые влияют на частоту переходов между уровнями кубита.

В самой простой, марковской модели модели шума, события декогеренции независимы во времени и пространстве. Флуктуационный сигнал \(S_f(t)\), связывающийся с трансмоном посредством члена гамильтониана типа \(\hat{V} = S_f(t) \hat{a}^\dagger\hat{a}\), будет случайным образом менять частоту кубита. Это приведет к набегу фазы

\[ \Delta \phi(t) = \int\limits_0^t S_f(t) \mathrm{d}t \]

на кубите. Если разложить флуктуационный сигнал по спектральным компонентам (то есть представить в виде Фурье-компонент), то получим

\[ \Delta \phi(t) = \int\limits_{-\infty}^{+\infty} \frac{S_f(\omega)}{\omega} \operatorname{cos}(\frac{\omega t}{2}) \mathrm{d}\omega. \]

Таким образом, наиболее существенным с точки зрения случайного набега фазы (то есть дефазировки) является низкочастотный шум. К таким флуктуационным сигналам может относиться, например, тепловая населенность считывающего резонатора.

Другой тип флуктуационного сигнала связывается с трансмоном посредством дополнительного члена в гамильтониана, имеющего вид \(\hat{V} = i \Delta \Omega_\downarrow \left(\hat{a} - \hat{a}^\dagger\right)\). Такой флуктуационный сигнал приводит к самопроизвольному возбуждению и релаксации кубита под действием внешней силы. Наиболее существенными являются шумы, частота которых отвечает частоте кубита.

Помимо внешних воздействий, которые можно представить как случайное слагаемое в гамильтониане, существуют также и воздействия, которые нельзя представить в таком виде, например обыкновенную релаксацию кубита без сопутствующего теплового возбуждения. Такой канал декогеренции отвечает случайному действию оператора уничтожения \(\hat{a}\). Таковым является, например, релаксация трансмона в управляющую линию, через которую выполняются однокубитные операции.

В общем случае, для всех типов марковского шума можно ввести оператор коллапса \(\hat{c}\) и константу декогеренции \(\gamma\). В случае релаксации, \(\hat{c} = \hat{a}, \gamma=1/T_1\). Для дефазировки \(\hat{c} = \hat{\sigma}_z, \gamma = 1/2T_{\phi}\).

Для того, чтобы измерить эффекты декогеренции на сверхпроводниковые кубиты, используют два основных типа эксперимента. Первый типа эксперимента заключается в возбуждении кубита и считывании его состояния спустя время \(t\). Эксперимент повторяется много раз с различным временем задержки \(t\); результат можно зафитовать экспонентой. Время затухания экспоненты в \(e\) будет временем релаксации \(T_1\).

Такое измерение нечувствительно к дефазировке кубита. Чтобы измерить влияние дефазировки, кубит помещают в состояние суперпозиции при помощью вращения вокруг оси \(x\) на угол \(\pi/2\), ждут время \(t\), делают вращение вокруг оси \(z\) на угол, пропорциональный длительности паузы \(t\), а затем еще поворачивают на угол \(\pi/2\) вокруг оси \(x\). В случае идеальной двухкубитной системы зависимость результата измерений от длительности паузы \(t\) будет синусоидальной; при наличии декогеренции в марковской модели осцилляции будут затухать экспоненциально, причем константа затухания \(T_2\) может быть выражена как \(\frac{1}{T_2} = \frac{1}{2T_1} + \frac{1}{T_\phi}\).

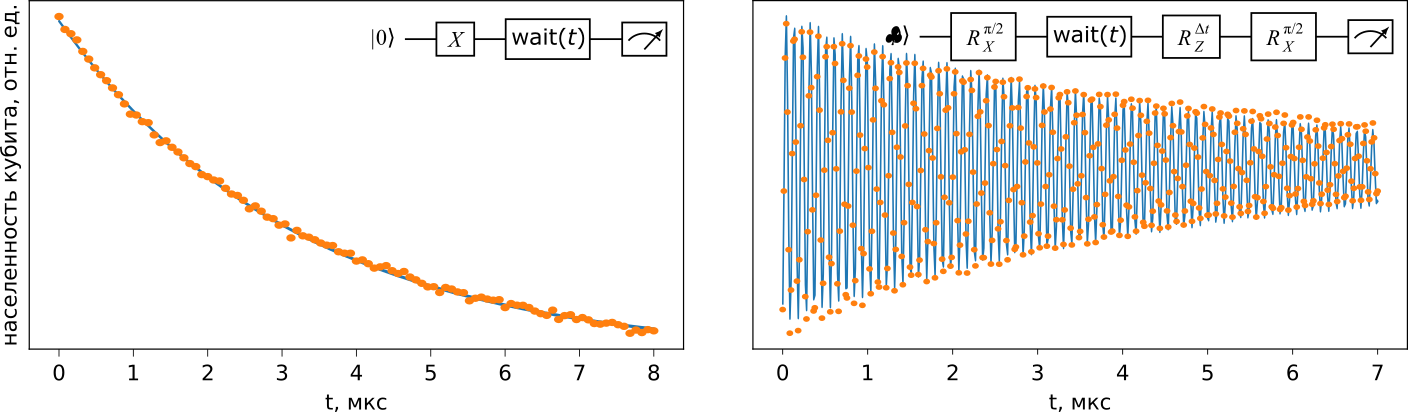
Fig. 53 Эксперименты по измерению времени когерентности кубита

Процессы декогеренции ограничивают длину алгоритмов, которые могут быть выполнены на сверхпроводниковом квантовом процессоре. Если хотя бы одно событие декогеренции произойдет в течение алгоритма, то результат выполнения может оказаться неправильным. Важно, что считывание в квантовом компьютере имеет принципиально дискретный характер: из-за этого в принципе возможно говорить о дискретных ошибках, а не о непрерывных ошибках, как в аналоговых компьютерах. Кроме того, как и в обычных цифровых компьютерах, в квантовых компьютерах возможна коррекция ошибок. Для того, чтобы измерить вероятность ошибки напрямую, используют рандомизированное тестирование (randomized benchmarking) квантовых вентилей.

Идея рандомизированного тестирования заключается в том, чтобы выполнять случайную последовательность операций, а зачем сравнивать результат ее выполнения с теоретическим. Существует ряд различных вариаций рандомизированного тестирования, которые отличаются тем, из какой совокупности берутся случайные последовательности. В самом простом случае используют вентили из группы Клиффорда – это такое подмножество логических операций, которые не образуют универсальный набор, но зато алгоритмы целиком состоящие только из таких вентилей можно быстро просимулировать на классическом компьютере даже при большом количестве кубитов. Кроме того, часто используют только такие последовательности вентилей, в конце которых система оказывается не в состоянии суперпозиции, а в определенном состоянии, например в состоянии \(|0\dots0\rangle\). Ошибки приводят к тому, что вероятность \(\langle F_n \rangle\) получить состояние \(|0\dots0\rangle\) экспоненциально убывает с увеличением длины последовательности вентилей \(N\):

\[ \langle F_n \rangle_\mathrm{seq}(N)\sim e^{-F_1n} \]

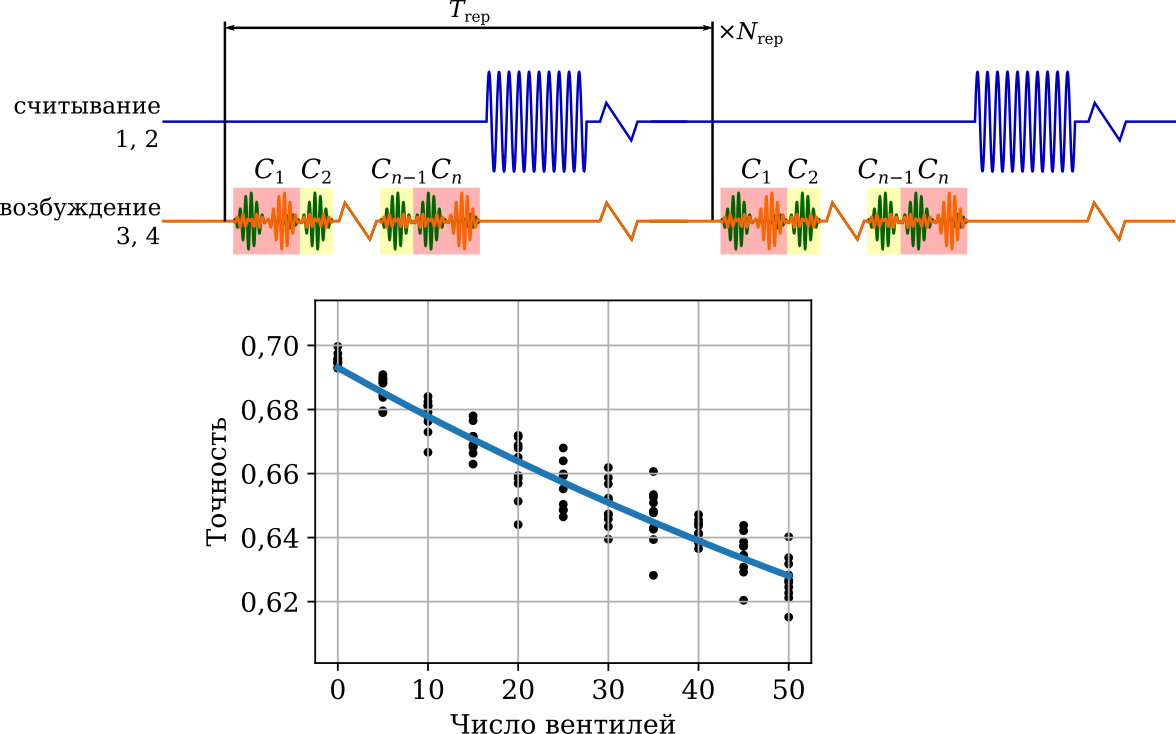
Fig. 54 Схема микроволновых импульсов и пример результатов рандомизированного тестирования вентилей из группы Клиффорда. Каналы 1 и 2 генератора сигналов произволной формы подключены к линии считывания, каналы 3 и 4 – к линии управления кубитом. Измерена населенность кубита после случайных последовательностей вентилей разных длин; константа экспоненциального затухания населенности дает точность в расчете на один вентиль \(F_1 = 0.993\).

Двухкубитные вентили

Для трансмонов существует целый ряд способов реализации двухкубитных операций. Как правило, для этого трансмоны связывают емкостным способом, напрямую или через элемент связи. Мы будем рассматривать двухкубитную операцию iSWAP, реализуемую при помощи параметрического изменения эффективной константы связи между кубитами.

Так же, как в случае кубита, связанного с резонатором, гамильтониан двух связанных трансмонов описывается в первом приближении соотношением

\[ \hat{H}/\hbar = \left( \omega_1+\frac{1}{2}\delta_q \left( \hat{a}^\dagger\hat{a}-1 \right) \right)\hat{a}^\dagger\hat{a} + \left( \omega_2+\frac{1}{2}\delta_r \left( \hat{b}^\dagger\hat{b}-1 \right) \right)\hat{b}^\dagger\hat{b} + \chi \left( \hat{a}^\dagger\hat{a}+\frac{1}{2} \right) \left( \hat{b}^\dagger\hat{b}+\frac{1}{2} \right), \]

где \(\hat{a}, \hat{a}^\dagger\) – операторы уничтожения и рождения одной степени свободы (трансмона), а \(\hat{b}, \hat{b}^\dagger\) – операторы другой степени свободы (трансмона).

Принцип работы элемента связи в том, что вместо одного джозефсоновского контакта, в нем есть два джозефсоновских контакта, соединенных параллельно. Такая цепь называется ПТ-СКВИД, или просто СКВИД (Superconducting Quantum Interference Device). Если у нас есть два джозефсоновских контакта в кольце, то такая структура будет вести себя по отношению к внешней цепи так же, как один контакт, но с управляемым критическим током. Управление критическим током можно осуществлять при помощи магнитного потока \(\Phi_x\), который проходит через кольцо СКВИДа. Соотношение для критического тока выглядит следующим образом:

\[ I_{\mathrm{C SQUID}}(\Phi_x) = \sqrt{\left(I_{\mathrm{Cc1}} + I_{\mathrm{Cc2}}\right)^2 \cos^2 \left( \pi\Phi_x/\Phi_0 \right) + \left(I_{\mathrm{Cc1}} - I_{\mathrm{Cc2}}\right)^2 \sin^2 \left( \pi\Phi_x/\Phi_0 \right)}. \]

Таким образом, элемент связи представляет собой слабо нелинейный LC-контур с перестраиваемой индуктивностью, а значит и частотой. В зависимости от его частоты будет менять эффективная константа связи между кубитами \(\chi\), а также – в меньшей мере – и остальные параметры системы.

Когда нет двухкубитной операции, желательно, чтобы кубиты не взаимодействовали, то есть \(\chi=0\). Все константы этого гамильтониана зависят от внешнего параметра – потока в СКВИДе элемента связи \(\Phi_x\). При быстром изменении этого параметра появляется дополнительное (диабатическое) слагаемое

\[ \hat{V} = i\hbar \hat{U}\frac{\partial \hat{U}^\dagger}{\partial \Phi_x}\frac{\partial \Phi_x}{\partial t} \sim \Omega\left(\hat{a}^\dagger + \hat{a}\right)\left(\hat{b}^\dagger + \hat{b}\right). \]

Мы не будем здесь подробно рассматривать природу этого слагаемого; подробнее об этом можно почитать, например, в работе [RGM+17]. Ограничимся тем, что это взаимодействие является поперечным, то есть \(xx\)-взаимодействием. Если модулировать поток в СКВИДе в резонансе с разностью частот между кубитами (\(n \omega_m = \omega_1 - \omega_2\), где \(n\) – номер гармоники), то возбуждение с одного кубита будет переходить на другой, и обратно.

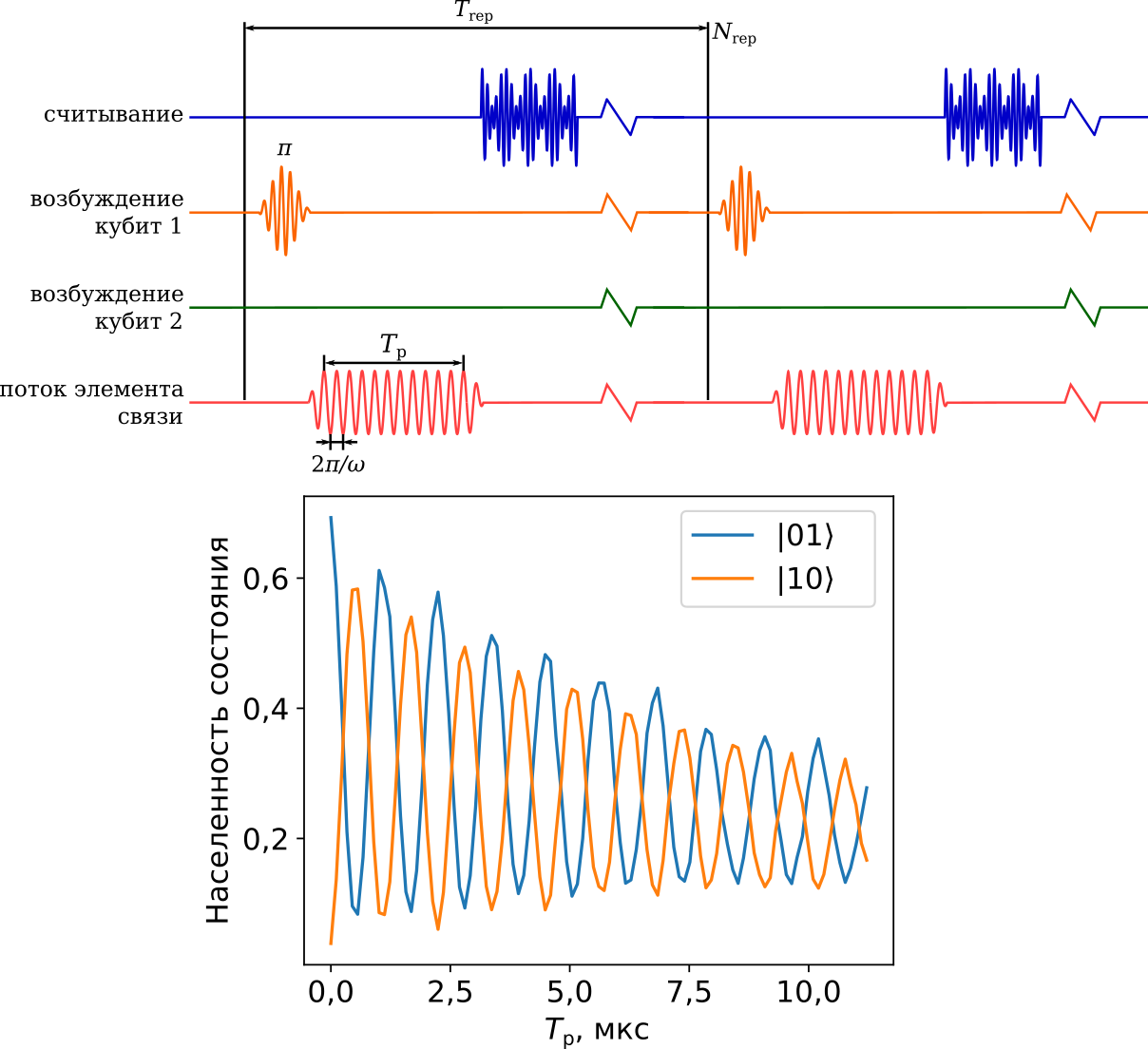
Fig. 55 Последовательность сигналов, которую нужно подать, чтобы наблюдать осцилляции населенности между кубитами, и результат из наблюдения. iSWAP получается при длительности вентиля \(T_p=500~\mathrm{ns}\)

Унитарная матрица этого вентиля имеет вид

\[\begin{split} \hat{U}(t) = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos\Omega_g t & i \sin \Omega_g t & 0 \\ 0 & i \sin \Omega_g t & \cos\Omega_g t & 0 \\ 0 & 0 & 0 & 1 \end{pmatrix}. \end{split}\]

Помимо вентиля iSWAP, на трансмонах делают CPHASE, который физически можно реализовать импульсным увеличением константы \(\chi\), или, например, как IBM Quantum Experience – при помощи кросс-резонансных вентилей.

Что почитать для дальнейшего изучения вопроса?

• Introduction to Quantum Computing and Quantum Hardware

• A Quantum Engineer’s Guide to Superconducting Qubits [KKY+19]