Квантово-классический SVM#

Автор(ы):

Описание лекции#

Лекция будет построена следующим образом:

  • посмотрим, как можно использовать VQC как ядро SVM;

  • напишем и применим код обучения смешанного SVM.

Перед тем как приступить, рекомендуется освежить материал по классическому методу опорных векторов, в частности, нужно понимать, как работает ядерный трюк.

VQC как ядерная функция#

Как мы много говорили в более ранних лекциях, квантовые схемы позволяют нам оперировать в гильбертовых пространствах волновых функций. Эти пространства имеют экспоненциально большую размерность, при этом они параметризуются линейным количеством параметров. А еще в этих пространствах определены скалярные произведения волновых функций, более того, именно результат выборки из скалярного произведения мы чаще всего и получаем как результат измерений!

Давайте попробуем посмотреть, что общего у VQC и ядер.

  • оба оперируют в пространстве большой (или бесконечной размерности);

  • и там, и там работа идет в гильбертовом пространстве и определено скалярное произведение;

  • и там, и там результат вычисляется как скалярное произведение.

Note

Это интересно, что многие специалисты в области QML сегодня даже предлагают вместо термина “квантовая нейросеть” использовать термин “квантовое ядро”, так как математически VQC гораздо ближе именно к ядрам, чем к слоям современных глубоких сетей.

Очевидная идея – попробовать как-то воспользоваться квантовой схемой, чтобы реализовать скалярное произведение двух классических векторов. Именно это и сделали авторы работы [HavlivcekCorcolesT+19].

Преобразование состояния#

На самом деле, если просто использовать какие-то простые квантовые операции, мы не получим какого-то преимущества над классическим ядерным SVM – ведь все то же самое можно будет сделать и на классическом компьютере.

Чтобы получить реальное преимущество, нам необходимо использовать запутывание и прочие “фишки” квантовых вычислений.

Дальше мы не станем изобретать велосипеды, а вместо этого воспользуемся примерами хороших преобразований из работы [SYG+20]. Рассмотрим, что именно там описано.

Общая схема#

Для простоты формул мы не будем выписывать обобщенные формулы, а все будем писать для нашего двумерного пространства. Тогда наша схема может быть разделена на несколько частей:

  • гейты Адамара и гейты \(CNOT\);

  • операции, основанные на элементах входного вектора;

  • попарные операции над парами элементов вектора.

Мы начинаем с того, что переводим кубиты в состояние суперпозиции, применяя операторы Адамара. Далее мы применяем однокубитные параметризованные операции и снова гейты Адамара. После этого мы применяем связку \(CNOT \to\) параметризованная парой операция \(\to CNOT\).

Выбор операции#

Следуя идее упомянутой статьи, в качестве что одно-элементной, что двух-элементной операции мы будем использовать гейт \(U_1\). Разница будет лишь в том, что мы передаем на вход в качестве параметра.

Feature function#

В качестве параметров на входе гейта \(U_1\), как мы уже говорили, выступают один или два элемента вектора \(x\). Строго это можно записать как функцию такого вида:

\[\begin{split} \phi(x_1, x_2) = \begin{cases} \phi(x),\text{ }x_1 = x_2 \\ \phi(x_1, x_2),\text{ }x_1 \neq x_2 \end{cases} \end{split}\]

Мы будем называть ее feature function. В некотором смысле можно сказать, что именно эта функция определяет тип ядра по аналогии с классическим SVM. В работе [SYG+20] описано много разных вариантов таких feature function, мы будем использовать следующую:

\[\begin{split} \begin{gathered} \phi(x) = x \\ \phi(x_1, x_2) = \pi \cos{x_1} \cos{x_2} \end{gathered} \end{split}\]

Скалярное произведение#

Все что мы описали выше, обозначим как квантовую схему \(U(x)\). Она преобразует нам вектор классических данных \(x\) в квантовое состояние \(\ket{\Psi}\). Но нам то нужно получить скалярное произведение \(\braket{U(x_1)|U(x_2)}\)! Выглядит сложно, но на самом деле существует эффективный способ получить эту величину без необходимости восстанавливать весь вектор состояния. Можно показать, что величина \(\braket{U(x_1)|U(x_2)}\) равна вероятности нулевой битовой строки (\(\ket{0, 0, ...., 0}\)) при измерении другой схемы: \(U(x_1)U(x_2)^\dagger\).

Все это может казаться сложным и запутанным, но должно стать гораздо понятнее, когда мы посмотрим на пример реализации от начала и до конца.

Пример реализации#

Схема#

Для начала необходимые импорты.

import pennylane as qml
from pennylane import numpy as np
from sklearn.datasets import make_moons

import matplotlib.pyplot as plt
%config InlineBackend.figure_format = 'retina'

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
  warnings.warn("Setuptools is replacing distutils.")

Помимо всех привычных, нам еще потребуется классический SVM из scikit-learn:

from sklearn.svm import SVC

Мы будем работать с уже привычным нам набором “Tow Moons”. Только в этом случае мы будем использовать чуть-чуть другую нормализацию – для нашего ядра элементы вектора \(x\) должны быть в интервале \([-1, 1]\). Сразу переведем наши данные в этот диапазон:

def normalize(x):
    """Переводит значения в интервал от -1 до 1"""

    return 2 * (x - x.min()) / (x.max() - x.min()) - 1

x_samples, y_samples = make_moons(n_samples=50)
y_samples = y_samples * 2 - 1

x_samples[:, 0] = normalize(x_samples[:, 0])
x_samples[:, 1] = normalize(x_samples[:, 1])

plt.figure(figsize=(4, 3))
cb = plt.scatter(x_samples[:, 0], x_samples[:, 1], c=y_samples)
plt.colorbar(cb)
plt.show()
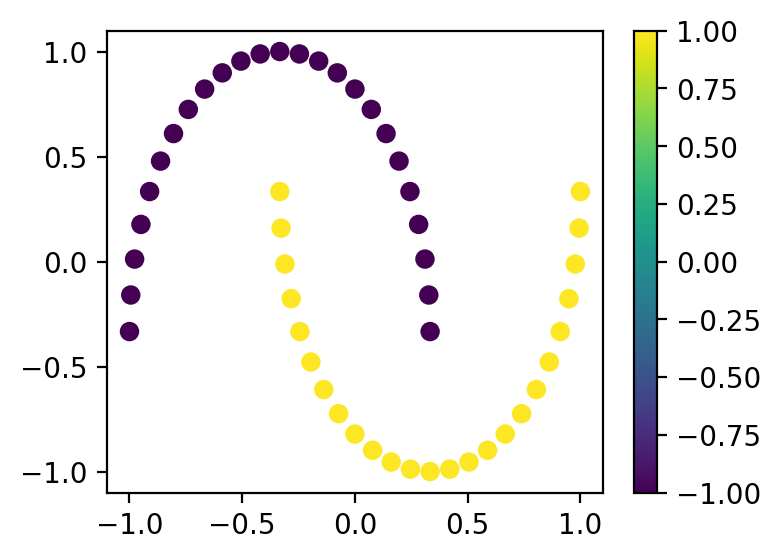
../../../_images/hybridsvm_6_0.png

И привычное нам объявление устройства.

dev = qml.device("default.qubit", 2)

Теперь давайте для начала реализуем наше преобразование над одним из векторов (\(U(x)\)).

def var_layer(x):
    qml.Hadamard(wires=0)
    qml.Hadamard(wires=1)

    qml.U1(x[0], wires=0)
    qml.U1(x[1], wires=1)

    qml.Hadamard(wires=0)
    qml.Hadamard(wires=1)

    qml.CNOT(wires=[0, 1])
    qml.U1(np.pi * np.cos(x[0]) * np.cos(x[1]), wires=1)
    qml.CNOT(wires=[0, 1])

А теперь реализуем

\[ \braket{U(x_1)|U(x_2)} = \bra{U(x_1)U(x_2)^\dagger \Psi} M_0 \ket{U(x_1)U(x_2)^\dagger \Psi}, \]

где \(M_0\) – проектор на один из собственных векторов системы кубитов, а именно на “нулевой”:

\[ M_0 = \ket{0, ..., 0}\bra{0, ..., 0}. \]

Проще говоря, мы реализуем схему, которая нам дает вероятности каждой из битовых строк (а дальше мы просто возьмем первую, она и отвечает строке \(0,...0\)):

@qml.qnode(dev)
def dot_prod(x1, x2):
    var_layer(x1)
    qml.adjoint(var_layer)(x2)

    return qml.probs(wires=[0, 1])

Ну и сразу вспомогательную функцию, которая нам считает то, что нам было нужно:

def q_dot_prod(x, i, j):
    x1 = (x[i, 0], x[i, 1])
    x2 = (x[j, 0], x[j, 1])

    return dot_prod(x1, x2)[0]

Для самопроверки убедимся в том, что наше “скалярное произведение” симметрично:

print(np.allclose(q_dot_prod(x_samples, 0, 1), q_dot_prod(x_samples, 1, 0)))

True

И сразу посмотрим на то, как выглядит наша схема:

print(qml.draw(dot_prod)(x_samples, y_samples))

 0: ──H──U1(M0)──H──╭C──────────╭C──╭C──────────────╭C──H──U1(-1)──H──╭┤ Probs 
 1: ──H──U1(M1)──H──╰X──U1(M2)──╰X──╰X──U1(-0.917)──╰X──H──U1(1)───H──╰┤ Probs 
M0 =
[-0.33333333  0.33333333]
M1 =
[-0.50587936  0.95456777]
M2 =
[2.59684003 1.71577697]

Гибридный SVM#

Мы не будем сами с нуля писать решение задачи квадратичного программирования, просто воспользуемся готовой рутиной из scikit-learn. Используемая там реализация позволяет вместо ядерной функции передать сразу матрицу Грама (Gram matrix). На самом деле это просто матрица всех попарных скалярных произведений наших векторов. Вычислим ее, сразу воспользовавшись тем, что

\[ \braket{U(x)|U(x)} = 1 \quad \text{и} \quad \braket{U(x_1)|U(x_2)} = \braket{U(x_2)|U(x_1)} \]
gram_mat = np.zeros((x_samples.shape[0], x_samples.shape[0]))

for i in range(x_samples.shape[0]):
    for j in range(x_samples.shape[0]):
        if i == j:
            gram_mat[i, j] = 1
        if i > j:
            r = q_dot_prod(x_samples, i, j)
            gram_mat[i, j] = r
            gram_mat[j, i] = r

Обучим нашу модель:

model = SVC(kernel="precomputed")
model.fit(gram_mat, y_samples)

SVC(kernel='precomputed')
In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.

Посчитаем предсказания и посмотрим на результат:

preds = model.predict(X=gram_mat)

plt.figure(figsize=(4, 3))
cb = plt.scatter(x_samples[:, 0], x_samples[:, 1], c=preds)
plt.colorbar(cb)
plt.show()
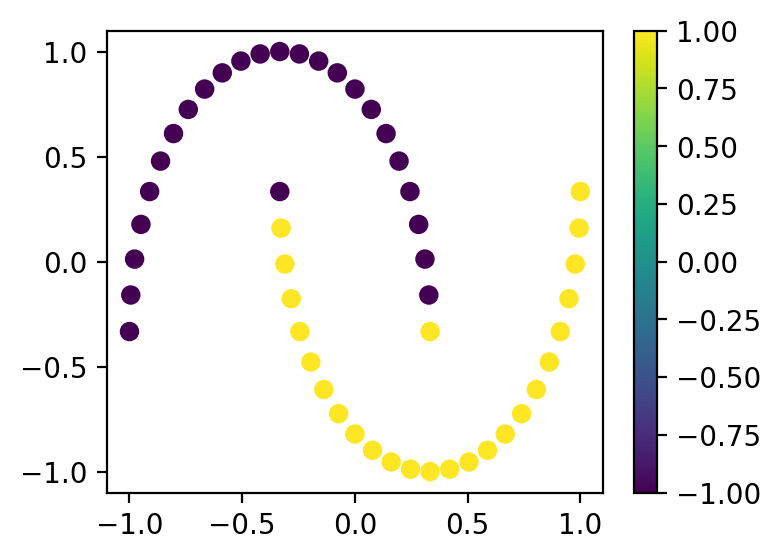
../../../_images/hybridsvm_24_0.png

Результат выглядит неплохо!

Заключение#

Расчет полной матрицы скалярных произведений дает нам сложность \(O(N^2)\) вызовов. Но основной потенциал гибридного SVM в том, что задачу квадратичной оптимизации на самом деле можно тоже решать на квантовом компьютере, используя алгоритм Гровера (про него рассказано в ранних лекциях), причем за сложность всего \(O(N)\) и без расчета полной матрицы Грама!

Многие считают, что NISQ квантовые компьютеры могут стать для SVM чем-то типа видеокарт для нейронных сетей и вернуть этот алгоритм на пьедестал лучших алгоритмов машинного обучения!