Обзор и классификация физических платформ для квантовых вычислений

Автор(ы):

• Беседин Илья

Радиочастотные и оптические кубиты

Первый признак, по которому можно классифицировать разные кубиты, это характер тех двух квантовых состояний, в которых хранится информация. Рассмотрим, например, фрагмент структуры уровней для иона Yb-171+ [Mon]. Этот ион часто используют для квантовых вычислений.

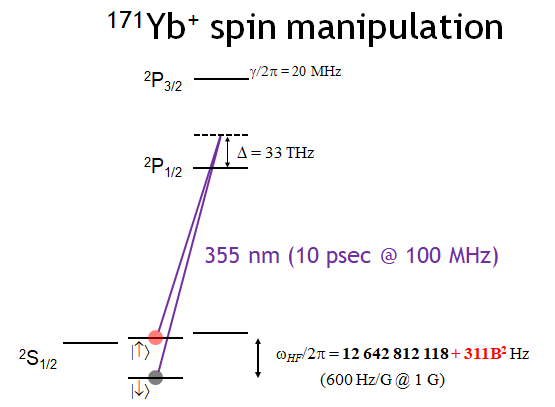
Fig. 39 Фрагмент структуры энергетических уровней иона Yb-171+. У типичного атома очень много степеней свободы: спин ядра, спин электронной подсистемы, радиус орбитали электрона и проекция момента орбитали электрона. Переходы между состояниями имеют очень разные частоты, времена когерентности и восприимчивости к частот к внешним полям. Чтобы сделать из иона кубит, надо определиться, какой уровень будет “0”, а какой – “1”.

На сегодняшнем этапе все платформы для квантовых вычислений можно разделить на два класса: те, которые работают со сравнительно низкими \(\omega/2\pi\sim10^{5}\dots10^{10}~\mathrm{Hz}\) частотами (вплоть до микроволновых), и те, которые работают на высоких частотах \(\omega/2\pi\sim10^{13}\dots10^{15}~\mathrm{Hz}\). К первым относятся:

• сверхпроводниковые квантовые схемы;

• кубиты на тонком и сверхтонком расщеплении в нейтральных атомах;

• кубиты на сверхтонком расщеплении в ионах;

• кубиты спинах в квантовых точках;

• кубиты на экзотических квазичастицах, вроде Майорановских фермионов.

К второй группе относятся:

• оптические и телекоммуникационные фотонах;

• кубиты на оптических переходах в атомах и ионах.

Квантовые компьютеры первого типа надо сильно охлаждать, так как они самовозбуждаются под действием броуновского движения и теплового излучения тел, находящихся при комнатной температуре.

Природа степени свободы для кодирования информации

Можно классифицировать популярные платформы для квантовых вычислений и по другим признакам. Например, есть кубиты на естественных степенях свободы и кубиты на коллективных степенях свободы.

Естественные степени свободы – это:

• любые переходы в уединенных атомах и ионах;

• фотоны в открытом пространстве.

Кубиты на естественных степенях свободы автоматически получаются одинаковыми: вы берете одинаковые атомы, и у них обязательно будут одинаковые переходы. Впрочем, если поместить их в какую-нибудь ловушку, то из-за того, что ловушки немного влияют на частоты переходов в атомах, эту эквивалентность легко испортить.

Fig. 40 Фотография уединенного атома в ловушке. Источник: [ion]

Кубиты на искусственных степенях свободы получаются когда имеет место коллективная динамика большого числа частиц, например поляризация в материала оптоволокна, или коллективное движение электронов в сверхпроводнике. Примеры искусственных степеней свободы:

• сверхпроводниковые электрические цепи;

• фотоны в интегрально-оптической схеме;

• фотоны в оптоволокне;

• спины в квантовых точках;

• любые квазичастицы в твердотельных системах.

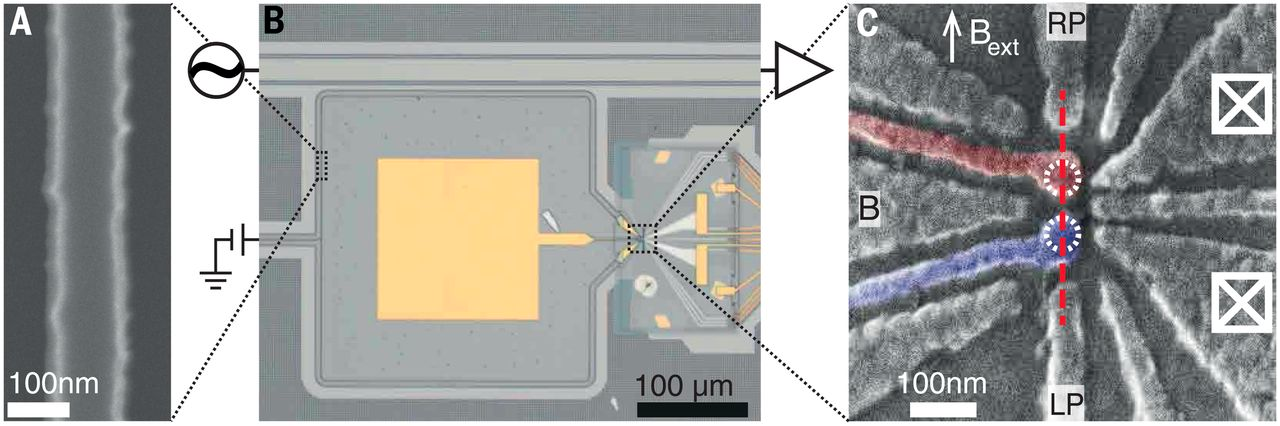
Fig. 41 Изображение кремниевой микросхемой с кубитом на квантовой точке. Источник: [SZK+18]

На самом деле граница между естественными степенями свободы и искусственными вовсе не такая очевидная, как может показаться на первый взгляд. Так, например, фотон, находящийся в открытом пространстве, можно поместить между двумя зеркалами, которые образуют резонатор. Но в таком случае в зеркалах, и в носителях заряда в зеркале будет храниться часть энергии фотона – получается так называемый “поляритон”, который уже не совсем естественная степень свободы. Абсолютно тождественными могут быть только те носители информации, которые ни с чем не связаны.

Способ кодирования информации

Только системы, где есть всего два уровня, а больше никакие не используются и не учитываются, строго говоря являются кубитами. Такими являются, например:

• потоковые сверхпроводниковые кубиты;

• логические кубиты, которые получаются выполнением кодов коррекции на большом числе физических кубитов любой природы.

Помимо “чистых” кубитов, у которых есть всего два дискретных состояния, существуют также “кудиты”, которые имеют \(d\) (\(d>2\)) состояний. Таковыми являются, например:

• ионы со сложной структурой уровней и правилами отбора переходов между ними;

• сверхпроводниковые кубиты-трансмоны;

• атомы и ридберговские состояния в них.

Fig. 42 Потенциал и уровни энергии в сверхпровониковом кубите-трансмоне. Построено с помощью scqubits [GK21]. Как правило используются нижние два уровня, однако и остальные уровни можно использовать для алгоритмов

Бывают модели квантовых вычислений на непрерывных степенях свободы, например:

• оптические вычисления на непрерывных переменных;

• колебательное движение ионов в радиочастотных ловушках;

• состояния микроволнового поля в сверхпроводниковых резонаторах.

Способ выполнения операций

Модели вычислений в квантовых компьютерах можно классифицировать по признаку способа реализации операций в них. Самый простой и очевидный способ – воздействие на кубит (кудит, непрерывную переменную) при помощи короткого аналогового сигнала на резонансной частоте этой системы, причем амплитуда и фаза этого сигнала будет определять унитарную матрицу операции. Так работают

• сверхпроводниковые кубиты-трансмоны и потоковые кубиты;

• кубиты на ионах в радиочастотных ловушках;

• кубиты на нейтральных атомах в дипольных ловушках.

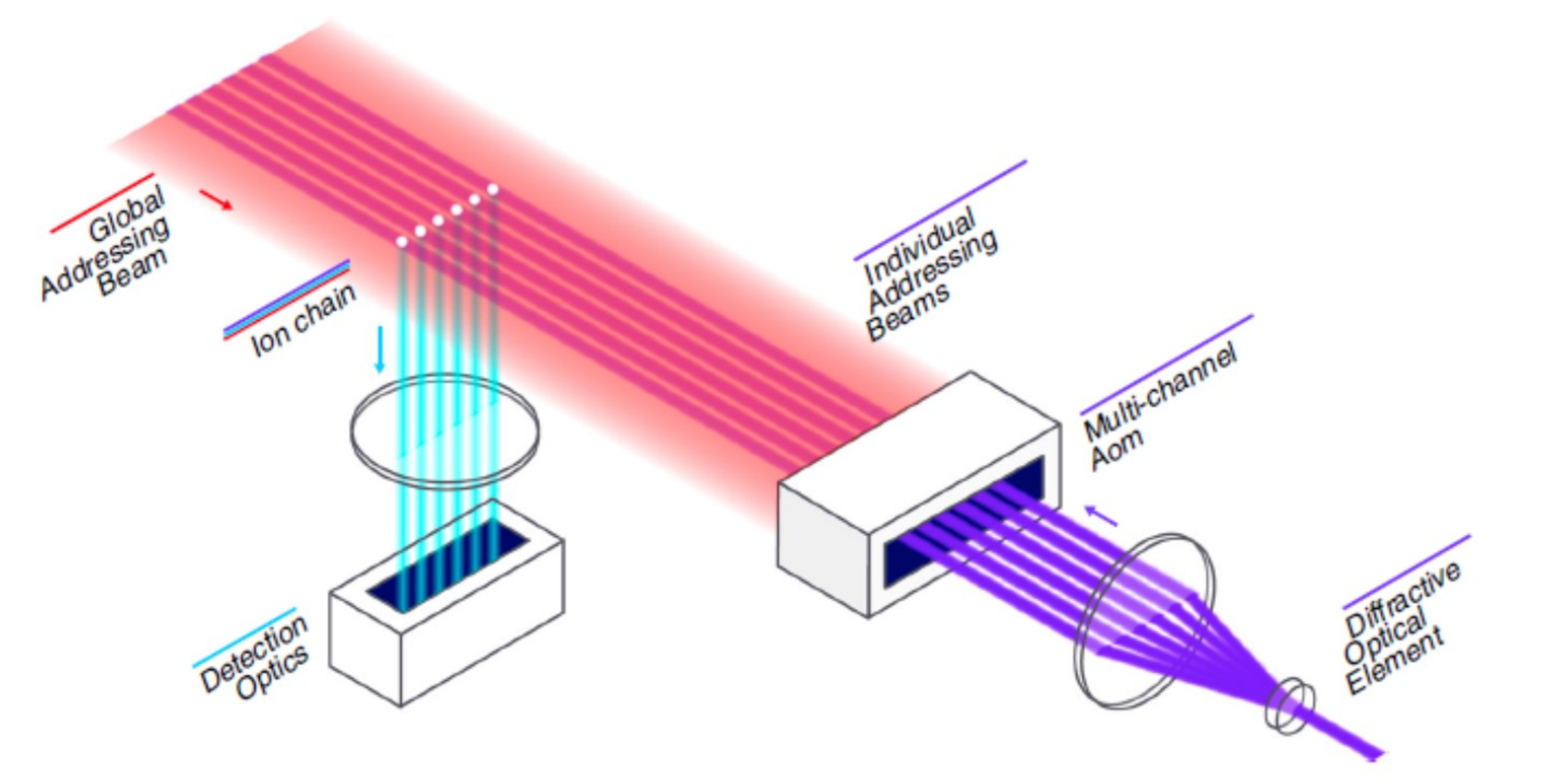
Fig. 43 Схема квантового компьютера на ионах. Источник: [WBD+19]. Кубиты расположены рядом друг с другом в вакуумной камере, а управляющие сигналы представляют собой лазерные лучи, направленные на каждый ион. Для однокубитных и двухкубитных операций используют разные лазеры, для считывания – еще лазер. Рассеянное на ионе излучение последнего лазера детектируется, чтобы определить состояние кубита. Похожим образом работают и кубиты на нейтральных атомах (там есть дополнительный оптический пинцет), и сверхпроводникые кубиты (там вместо лазеров используются микроволновые кабели).

Бывают вычислительные модели, в которых вместо временной последовательности управляющих сигналов носитель информации движется по “конвейеру”, вдоль которого с ним выполняются операции. Так работают, например, вычисления на:

• фотонах в интегральной оптике;

• фотонах в открытом пространстве.

Некоторые модели вычислений вовсе не предполагают выполнения каких-то изолированных операций. Впрочем, для таких моделей вычислений и не выполняется большинство утверждений и теоретических предсказаний, связанных с квантовыми вычислениями. Таковыми моделями является, например, квантовый аннилер D-Wave. Важно отметить, что классические компьютеры работают совсем иначе, чем все вышеперечисленные квантовые компьютеры. В них операции осуществляются цифровыми сигналами, то есть от непосредственного значения уровня сигнала слабо зависит то, какая операция будет выполнена, главное, чтобы сигнал вовремя превысил некоторое пороговое значение. Цифровой характер классических компьютеров имеет очень важное значение для масштабирования алгоритмов, ведь именно он обеспечивает воспроизводимость и возможность безошибочной работы квантового компьютера. К моделям квантовых вычислений, нечувствительным к аналоговым ошибкам управляющих сигналов, или с пониженной чувствительностью к ним, можно отнести:

• кубиты на майорановских фермионах;

• логические кубиты, которые получаются в результате работы алгоритмов квантовой коррекции ошибок на физических кубитах любой природы;

• сверхпроводниковые 0-пи кубиты, при условии, что гейты будут производиться специальным помехозащищенным образом, а не через промежуточные уровни.

Наборы инструкций и универсальность

Разные модели вычислений дают разные наборы инструкций для реализации квантовых алгоритмов. В зависимости от вероятности успешной реализации инструкций (квантовые компьютеры делают ошибки!) эти модели вычислений могут быть ближе, либо дальше от создания универсального масштабируемого квантового компьютера. По этому признаку:

• сверхпроводниковые кубиты;

• нейтральные атомы;

• ионы в радиочастотных ловушках

являются самыми очевидными. Набор инструкций в них содержит однокубитные и двухкубитные операции, инициализацию кубита в определенном состоянии и считывание. Чем выше точность операций – тем лучше, и все операции на сегодняшний день продемонстрированы с вероятностью положительного исхода выше 99% – этого все еще мало для многих применений, но это уже что-то.

Для вычислений на линейнооптических схемах используются источники единичных эквивалентных фотонов, либо источники запутанных фотонов, либо источники сжатого света. Вероятность успеха операции по созданию такого излучения (либо степень сжатия света) на сегодняшний день сильно далека от того, что нужно для универсальности квантовых вычислений; здесь идет речь о сжатии порядка 10 дБ (грубо переводя на язык “успешного выполнения операции” 0,9), и вероятности испускания фотона 0,9. Однако отсутствие универсальности не означает, что линейнооптические схемы должны быть для всех задач вычислительно слабее, чем другие платформы: напротив, самое сильное квантовое превосходство на сегодняшний день достигнуто именно на таких устройствах.

Причина, по которой линейнооптические системы выделяются среди других заключается в том, что для полноценного компьютера (что классического, что квантового) нужны нелинейные элементы. В классическом компьютере это транзисторы. На одних линейных индуктивностях и емкостях можно, в зависимости от способа кодирования информации, выполнять какой-то набор операций, но универсальным он не будет, потому что функция отклика линейной цепи является линейным. Алгоритмы, которые не сводятся к умножению матрицы на вектор в некотором представлении данных, на линейной системе выполнить не получится. Чтобы обойти это ограничение, линейно-оптические системы для квантовых вычислений принимают на часть своих входов, в дополнение к входным данным, сложные неклассические сигналы, а на выходе производится считывание числа фотонов, которое является квадратичным по отношению к амплитудам сигналов. Дополнение линейной оптики наборами нелинейных операций может сделать такие модели вычислений универсальными.

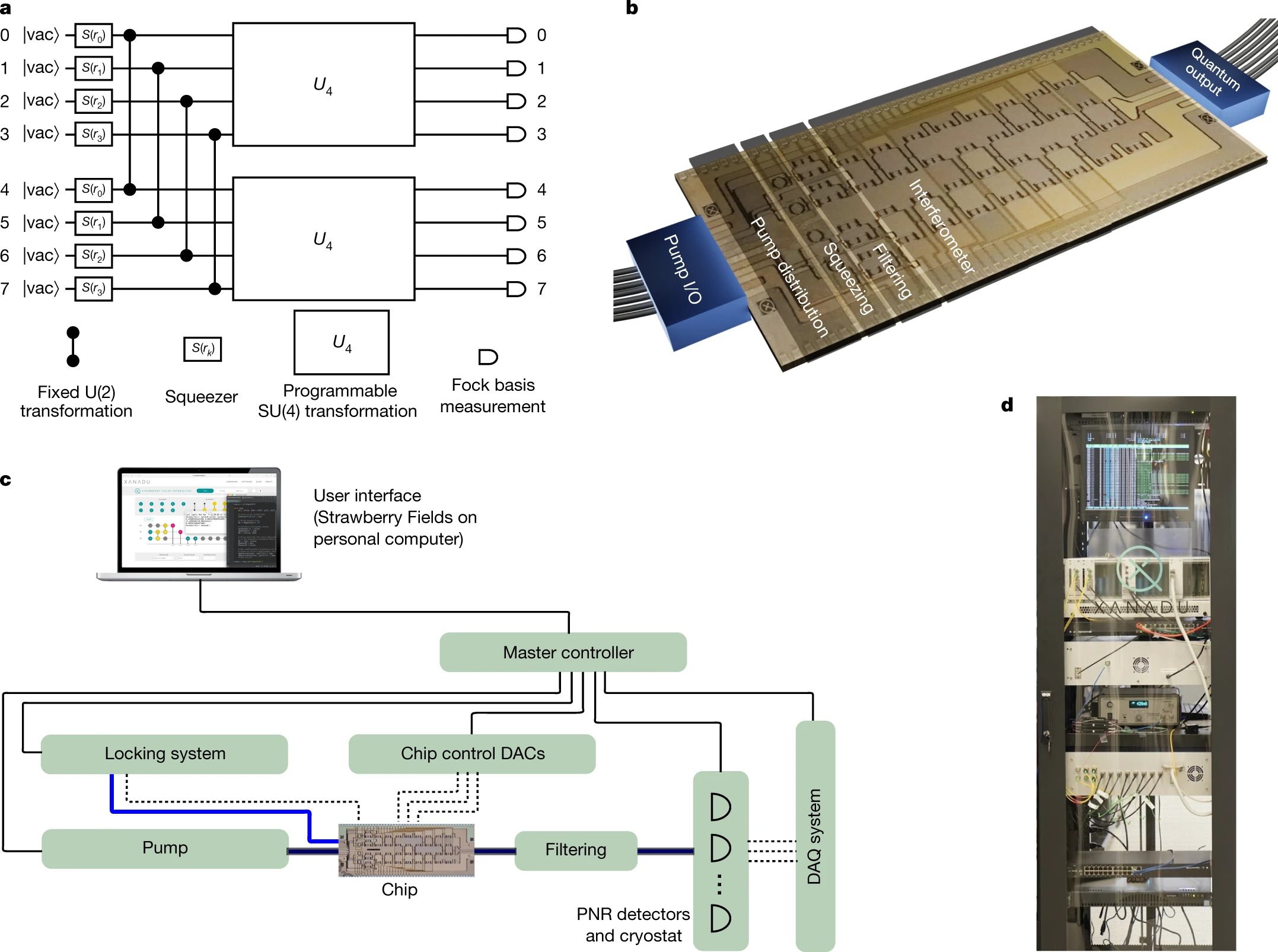
Fig. 44 Принципиальная схема работы оптического квантого чипа Xanadu. Вязто из работы [ABBradler+21]. a – квантовый алгоритм, выполняемый схемой: 1) сжатие света до 8 модах и создание запутанности (формирование двухмодового сжатового состояния света, эквивлент однокубитных гейтов), 2) программируемые двухкубитные гейты в каждом четырехмодовом подпространстве, 3) считывание всех 8 мод в фоковском базисе; b – изображение чипа, на котором видны основные модули; c – схема управляющих сигналов и приборов; d – фотография всей системы (кроме управления детектором фотонов) в серверной стойке.

Наконец, кубиты с дискретными операциями, такие как логические кубиты и кубиты на майорановских фермионах, сами по себе не дают полный набор квантовых логических операций – в дополнение к ним нужны обычные кубиты. Впрочем, задача построения кубита на майорановских фермионах или на коррекции ошибок сама по себе настолько сложная, что необходимость связать с ним обыкновенные дополнительные кубиты не кажется такой сложной.

Успехи в практической реализации

Платформы для квантовых вычислений можно отсортировать по максимальному размеру гильбертова пространства и точности операций (не только унитарных гейтов, но и считыванию и инициализации), которое удавалось реализовать экспериментально. В этом рейтинге только три верхние платформы находятся относительно близко к режиму квантового превосходства в подтвержденных экспериментальных работах. Итак, рейтинг:

• линейная оптика (фотоны) в открытом пространстве;

• сверхпроводниковые кубиты-трансмоны;

• ионы в линейных радиочастотных ловушках;

• интегральнооптические фотоны;

• нейтральные атомы в дипольных ловушках;

• спины в квантовых точках.

Другие платформы существуют на сегодняшний день в лучшем случае в виде двухкубитной системы, чаще – одного кубита, а лучше вообще в виде теоретической концепции – которая может оказаться вовсе нереализуемой на практике.