Алгоритм HHL#

Автор(ы):

Сегодня пришла пора поговорить о знаменитом алгоритме Харроу, Хассидима и Ллойда, более известном как HHL-алгоритме, способном решать системы линейных уравнений.

Очень надеюсь, что к данному занятию у вас уже есть представление об алгоритме фазовой оценки (QPE), использующем обратное квантовое преобразование Фурье, на котором и базируется HHL. Глубокое понимание всех тонкостей этого алгоритма потребует от вас уверенного владения математическим аппаратом. За детальным описанием вы всегда можете обратиться к статьям [DHM+18], [HHL09], и [HZL+17]. Приготовьтесь потратить время и умственные ресурсы, если алгоритм вас зацепит и вы решите в нем как следует покопаться. Мы же поможем вам заинтересоваться, рассмотрим основные принципы и небольшой пример.

Note

Именно HHL-алгоритм произвел настоящую революцию в области квантового машинного обучения. Ведь решение систем линейных уравнений так или иначе находится “под капотом” почти любого известного алгоритма машинного обучения. И действительно:

классические линейная и логистическая регрессия сводятся именно к этой задаче;
задача SVM может быть переформулирована в терминах решений систем линейных уравнений;
задача нахождения обартной матрицы (часто используется в глубоком обучении) внутри обычно решается через решение линейной системы;

И это только малая часть примеров!

Так что знакомство с QML не будет полным без ознакомления с этим прекрасным, но очень сложным алгоритмом!

../../../_images/614px-Seth_Lloyd.jpg — Fig. 64 Сет Ллойд, профессор MIT и один из создателей HHL-алгоритма#

Задача#

Представим обычную систему линейных уравнений:

\begin{array}{r} {\begin{cases} a_{11} x_{1} + a_{12} x_{2} = b_{1} \\ a_{21} x_{1} + a_{22} x_{2} = b_{2} \end{cases} \end{array}

Что в операторной форме можно переписать как:

A \vec{x} = \vec{b},

где $A$ – эрмитова матрица.

Мы будем решать задачу на квантовом компьютере, то нам нужно перейти к квантовым состояниям:

A | x ⟩ = | b ⟩

Чтобы найти искомый вектор $| x ⟩$ , все что нам по сути нужно сделать – это найти обратный к $A$ оператор (обозначаемый $A^{- 1}$ ), который находится из равенства:

A A^{- 1} = A^{- 1} A = I

Распишем применительно к нашей задаче поиска вектора $| b ⟩$ :

\begin{array}{r} A | x ⟩ = | b ⟩ \\ A^{- 1} A | x ⟩ = A^{- 1} | b ⟩ \\ | x ⟩ = A^{- 1} | b ⟩ \end{array}

Оказывается, что и это все можно провернуть с помощью известных квантовых преобразований. Принципиальный вид нашей схемы представлен следующим образом:

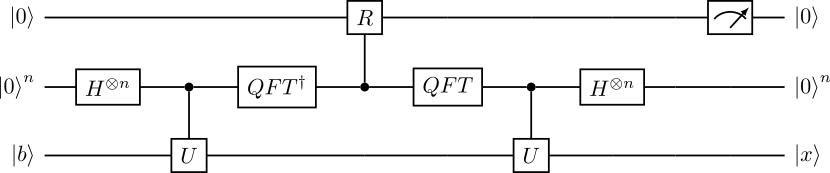
../../../_images/hhl_circuit.png — Fig. 65 Квантовая схема, реализующая алгоритм HHL#

В нижний регистр загружается вектор $| b ⟩$ , средний и нижний регистры участвуют в фазовой оценке, а верхний дополнительный кубит нужен для так называемого вращения, обусловленного собственными значениями. Давайте разбираться.

Реализация HHL#

Для начала мы должны подготовить наши регистры по всем квантовым законам: $| b ⟩$ и $| x ⟩$ должны быть пронормированы, а оператор $A$ должен быть эрмитовым. Надеемся, что Вы помните про ортонормированный базис, сферу Блоха, комплексное представление векторов $| 0 ⟩$ и $| 1 ⟩$ … Если нет, то обратитесь к предыдущим разделам курса.

Мы будем использовать оператор $U = e^{i A t}$ , и нужно, чтобы он был обратим –- для этого $А$ должна быть эрмитовой.

Note

В случае, когда $A$ не является эрмитовой, нужно перейти к эрмитовой матрице $C$ :

\begin{array}{r} C = (\begin{array}{c} 0 & A \\ A^{†} & 0 \end{array}) \end{array}

И рассматривается задача $C \vec{y} = (\begin{array}{l} \vec{b} \\ 0 \end{array})$ для того, чтобы найти решение $y = (\begin{array}{l} 0 \\ \vec{x} \end{array})$

Вспомним, что эрмитову матрицу $A$ можно представить в виде суммы собственных векторов, умноженных на собственные значения, т.е. в виде спектрального разложения:

\begin{array}{r} \begin{aligned} A = \sum_{j = 0}^{N - 1} λ_{j} | u_{j} ⟩ ⟨ u_{j} | \\ A^{- 1} = \sum_{j = 0}^{N - 1} λ_{j}^{- 1} | u_{j} ⟩ ⟨ u_{j} | \end{aligned} \end{array}

Тогда вектор $| b ⟩$ можно представить через собственные векторы $A$ :

| b ⟩ = \sum_{j = 0}^{N - 1} b_{j} | u_{j} ⟩

Чтобы понять, почему это тоже ключевой момент, давайте вспомним, что значит собственный вектор и собственное значение матрицы.

Note

Собственным вектором $| u ⟩$ оператора $A$ называется такой ненулевой вектор, для которого выполняется:

A | u ⟩ = λ | u ⟩

$λ$ – собственное значение оператора $A$ .

Таким образом, искомый вектор $| x ⟩$ – не что иное, как:

| x ⟩ = A^{- 1} | b ⟩ = \sum_{j = 0}^{N - 1} λ_{j}^{- 1} b_{j} | u_{j} ⟩

Итак, фазовая оценка. Мы применяем к кубитам второго регистра матрицы Адамара, тем самым приводим их в суперпозицию. Следом запускаем оператор $U$ :

U = e^{i A t} = \sum_{j = 0}^{N - 1} e^{i λ_{j} t} | u_{j} ⟩ ⟨ u_{j} |

Для того, чтобы узнать собственное значение оператора $U$ , получения фазы (Quantum Phase Estimation – QPE), результатом которого получится следующее состояние:

Q P E (U, | 0 ⟩ | u ⟩) =

\frac{1}{2^{m / 2}} (| 0 ⟩ + e^{2 π i 2^{m - 1} ψ} | 1 ⟩) \otimes (| 0 ⟩ + e^{2 π i 2^{m - 2} ψ} | 1 ⟩) \otimes \dots \otimes (| 0 ⟩ + e^{2 π i 2^{0} ψ} | 1 ⟩) \otimes | u ⟩ =

\frac{1}{2^{m / 2}} \sum_{j = 0}^{2^{m - 1}} e^{2 π i ψ j} | j ⟩ | u ⟩ = | ψ_{u} ⟩ | u ⟩

Параметр $t$ это нормировочная константа в случае $U = e^{i A t}$ :

e^{2 π i ψ} = e^{i λ_{j} t}

ψ = \frac{λ_{j} t}{2 π}

Параметр $t$ подбирается с учетом того, что на выходе алгоритма QPE собственные значения $λ_{j}$ нормализуются к виду $0 \leq λ_{j} \leq 1$ и обычно мы располагаем ограниченным числом кубитов, которое можно использовать для аппроксимации.

Алгоритм обратного квантового Фурье переводит фазу в конкретный вектор.

Принципиальная схема QPE выглядит следующим образом:

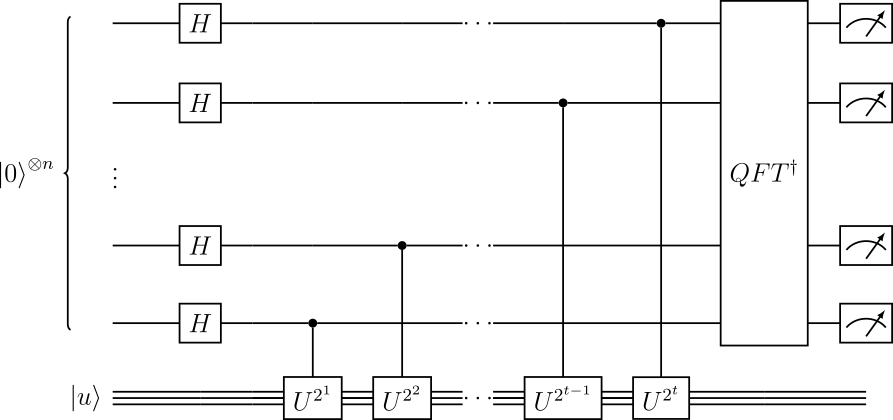
../../../_images/hhl_circuit2.png — Fig. 66 Схема алгоритма QPE#

Итак, мы подготовились, вспомнили много хорошего, теперь пошагово распишем наш алгоритм.

Стартуем мы со следующим состоянием:

| 0 ⟩_{a} | 0 ⟩_{r} | b ⟩_{m}

Т.е. наше состояние будет храниться в трех регистрах, в каждом из которых содержится столько кубитов, сколько нужно для решения задачи.

Применение QPE с использованием преобразования $e^{i A t}$ , после чего мы получим собственное значение оператора $A$ во втором регистре:

$| 0 ⟩_{a} | 0 ⟩_{r} | b ⟩_{m} \to \sum_{j = 0}^{N - 1} b_{j} | 0 ⟩_{a} | λ_{j} ⟩_{r} | u_{j} ⟩_{m}$
Поворачиваем первый кубит (с индексом $a$ ), используя специальный оператор вращения $R$ :

$R | 0 ⟩_{a} = \sum_{j = 0}^{N - 1} (\sqrt{1 - \frac{C^{2}}{λ_{j}^{2}}} | 0 ⟩_{a} + \frac{C}{λ_{j}} | 1 ⟩_{a}),$

где $C$ – константа, которая должна быть меньше минимального из лямбда: $| C | < λ_{m i n}$ [Почему?].

Переводим первый кубит $| 0 ⟩_{a}$ :

$\sum_{j = 0}^{N - 1} b_{j} | 0 ⟩_{a} | λ_{j} ⟩_{r} | u_{j} ⟩_{m} \to$

$\sum_{j = 0}^{N - 1} (\sqrt{1 - \frac{C^{2}}{λ_{j}^{2}}} | 0 ⟩ + \frac{C}{λ_{j}} | 1 ⟩) b_{j} {| λ_{j} ⟩}_{n} {| u_{j} ⟩}_{m}$
Применяем $Q P E^{†}$ (т.е. обратное получение фазы) и получаем следующее состояние:

$\sum_{j = 0}^{N - 1} (\sqrt{1 - \frac{C^{2}}{λ_{j}^{2}}} | 0 ⟩ + \frac{C}{λ_{j}} | 1 ⟩) b_{j} | 0 ⟩_{n} {| u_{j} ⟩}_{m}$

В конце мы измеряем верхний кубит и если получаем единицу, то знаем, что в нижнем регистре хранится искомый $| x ⟩$ с учетом нормировки:

$| x ⟩ \approx \sum_{j = 0}^{N - 1} C (\frac{b_{j}}{λ_{j}}) | u_{j} ⟩$

Пример#

Рассмотрим небольшой, но удобный пример. Удобный в том отношении, что, вообще говоря, алгоритм HHL имеет определенное приближение. Если собственные значения не представимы в бинарной форме, то о 100% точности говорить не приходится. Мы также опустим ряд вопросов, связанных с подбором параметров и количества кубитов второго регистра. Главное сейчас – понять, что происходит, и для этого наша матрица $А$ эрмитова, все условия подобраны, а преобразования точны. Стоит помнить, что знать заранее значение собственных векторов и собственных значений нам совершенно не обязательно – это нужно лишь для наглядности.

Итак, пусть задача выглядит так :

\begin{array}{r} \begin{aligned} A = (\begin{array}{ll} 1 & \frac{3}{5} \\ \frac{3}{5} & 1 \end{array}) \\ | b ⟩ = | 1 ⟩ = [\begin{matrix} 0 \\ 1 \end{matrix}] \end{aligned} \end{array}

\begin{array}{r} {\begin{cases} x_{1} + \frac{3}{5} x_{2} = 0 \\ \frac{3}{5} x_{1} + x_{2} = 1 \end{cases} \end{array}

Собственные значения и соответствующие собственные векторы:

\begin{array}{r} \begin{aligned} λ_{0} = \frac{2}{5}, | u_{0} ⟩ = [\begin{array}{c} - 1 \\ 1 \end{array}] \\ λ_{1} = \frac{8}{5}, | u_{1} ⟩ = [\begin{matrix} 1 \\ 1 \end{matrix}] \end{aligned} \end{array}

Зададим параметр $t$ и проанализируем фазу:

t = 2 π \frac{5}{16}

e^{2 π i ψ} = e^{i λ_{j} t}

ψ = \frac{λ_{j} t}{2 π}

\frac{λ_{0} t}{2 π} = \frac{1}{8}, \frac{λ_{1} t}{2 π} = \frac{1}{2}

Как мы видим, для перевода угла $ψ$ в векторную форму, нам понадобятся три кубита. После преобразования QPE мы имеем следующее состояние:

\begin{aligned} Q P E (| 0 ⟩_{a} | 0 ⟩_{r} | b ⟩_{m}) = \sum_{j = 0}^{1} \frac{1}{\sqrt{2}} | 0 ⟩_{a} | λ_{j} ⟩_{r} | u_{j} ⟩ = \frac{1}{\sqrt{2}} (| 0 ⟩_{a} | 001 ⟩_{r} | u_{0} ⟩ + | 0 ⟩_{a} | 100 ⟩_{r} | u_{1} ⟩) \end{aligned}

Подберем константу $C$ (как мы помним, она должна быть меньше наименьшего из собственных чисел) и произведем вращение:

\begin{array}{r} \begin{aligned} \frac{1}{\sqrt{2}} (\sqrt{1 - \frac{(1 / 16)^{2}}{(1 / 8)^{2}}} | 0 ⟩ + \frac{1 / 16}{1 / 8} | 1 ⟩) | 001 ⟩_{r} {| u_{0} ⟩}_{m} + \\ + \frac{1}{\sqrt{2}} (\sqrt{1 - \frac{(1 / 16)^{2}}{(1 / 2)^{2}}} | 0 ⟩_{a} + \frac{1 / 16}{1 / 2} | 1 ⟩_{a}) | 100 ⟩_{r} | u_{1} ⟩_{m} \end{aligned} \end{array}

В конце мы производим измерение верхнего кубита (с индексом $a$ ) и при получении единицы можем быть уверены, что нижний регистр содержит искомое решение с учетом нормировки:

\begin{array}{r} \begin{matrix} \frac{1}{2 \sqrt{2}} | 1 ⟩_{a} | 000 ⟩_{r} {| u_{0} ⟩}_{m} + \frac{1}{8 \sqrt{2}} | 1 ⟩_{a} | 000 ⟩_{r} {| u_{1} ⟩}_{m} \end{matrix} \end{array}

| x ⟩ \approx \frac{1}{2 \sqrt{2}} / (\sqrt{\frac{17}{128}}) | u_{0} ⟩ + \frac{1}{8 \sqrt{2}} / (\sqrt{\frac{17}{128}}) | u_{1} ⟩

QMLCourse

Алгоритм HHL

Contents

Алгоритм HHL#

Задача#

Реализация HHL#

Пример#