Смешанные состояния и матрицы плотности
Contents
Смешанные состояния и матрицы плотности#
Автор(ы):
Описание лекции#
Из этой лекции мы узнаем:
Что такое матрица плотности
Как ввести в описание квантовых состояний новый уровень случайности
Как связаны смешанные (mixed) и запутанные (entangled) состояния
Как можно описать насколько “сильно” квантовое состояние является смешанным
Смешанные состояния#
Эта глава кратко рассматривает довольно сложный, но крайне важный аспект квантового описания мира: как описать квантовую систему, в которой случайным является не только результат измерения, но и само состояние квантовой системы, иными словами, когда мы не можем описать квантовую систему определенным вектором состояния.
Как могут появиться такие ситуации?
Прежде всего, в любой реалистичной ситуации квантовая система будет испытывать влияние окружающей среды. Это воздействие окружающей среды на квантовый компьютер, как правило, может быть охарактеризовано некоторой температурой этой самой среды и скоростью термализации системы с ней. В отличие от классических компьютеров, где шумы редко приводят к ошибкам в вычислениях, квантовые компьютеры очень плохо защищены от шумов. Любое масштабное квантовое вычисление является гонкой с процессами декогеренции и релаксации: за время выполнения алгоритма шумы не должны испортить результат вычислений настолько, чтобы его нельзя было использовать.
Вторая, более важная причина использования смешанных состояний состоит в их тесной связи с запутанными состояниями, как показано ниже.
Почему нельзя обойтись волновой функцией#
Рассмотрим реальный физический кубит в состоянии равновесия, например, спин ядра атома в магнитном поле. Статистическая физика говорит нам, что вероятность обнаружить этот спин ориентированным вдоль внешнего поля выше, чем в противоположном полю направлении. Для расчета отношений этих вероятностей можно использовать распределение Больцмана: \(p_\uparrow/p_\downarrow = e^{\frac{2\mu \Delta H}{k_\mathrm{B}T}}\), где \(2\mu \Delta H\) – разность энергий состояний со спином вдоль поля и в противоположном полю направлений, \(k_B\) – постоянная Больцмана, а \(T\) – температура. Так как состояний у этой системы всего два, сумма их вероятностей должна давать единицу: \(p_\uparrow + p_\downarrow = 1\). Таким образом, вероятности состояний однозначно определены.
Волновую функцию, отвечающую такому тепловому состоянию, можно записать в виде
где значение фазы \(\phi\) не определено. Однако \(\phi\) определяет поведение системы не в меньшей мере, чем вероятности \(p_\uparrow\) и \(p_\downarrow\). \(\phi\) может равновероятно принимать любые значения. Таким образом, уже даже состояние теплового равновесия нельзя описать одной волновой функцией – это будет распределением вероятности по волновым функциям с разным \(\phi\).
Матрица плотности#
Оказывается, что вместо распределения вероятностей по волновым функциям можно использовать более простую конструкцию – матрицу плотности. Если система находится в состояниях \(\Phi_n\) с вероятностями \(p_n\), то матрицу плотности можно определить как
Выражение \(\ket{\Phi_n}\bra{\Phi_n}\) обозначает произведение вектора-столбца на вектор-строку – результатом будет матрица. Важно, что значение любой ожидаемой величины (отвечающей оператору \(\hat{A}\)) можно записать через \(\rho\):
Математическое обоснование этой циклической перестановки можно получить, расписав матричные произведения покомпонентно:
Любую наблюдаемую физическую величину можно выразить в виде ожидаемой величины некоторого эрмитова оператора – а значит, описание с помощью матрицы плотности является универсальным для любых случайных квантовых систем.
Стоит заметить, что матрица плотности для подсистем была впервые введена в научный оборот знаменитым советским физиком, лауреатом Нобелевской премии Львом Ландау. [15a]
Fig. 25 Лев Ландау, 1908-1968#
Чистые и смешанные состояния#
Состояния, которые описываются одной единственной волновой функцией \(\Psi\), называются чистыми (англ. pure states). Для таких состояний выражение для матрицы плотности получается тривиальным:
Матрица плотности чистого состояния является оператором-проектором: действие оператора на волновую функцию произвольного состояния \(\Phi\) дает проекцию \(\Phi\) на \(\Psi\). Состояния, которые нельзя описать одним вектором состояния, а можно лишь матрицей плотности, называются смешанными (англ. mixed states).
Чистота состояния#
Можно легко показать, для оператора-проектора (2) выполняется тождество
и следовательно, для чистого состояния
(напомним, что мы всегда считаем вектора состояния нормированными на единицу).
Аналогичным образом, но после более длинных выкладок можно показать, что в общем случае
причем знак равенства в последней формуле возможен, только если в формуле (1) сумма имеет лишь одно слагаемое (т.е. состояние является чистым). Последнее свойство матрицы плотности позволяет ввести ряд величин, характеризующих смешанные и запутанные состояния, о чем будет рассказано в заключительном разделе этой лекции. Величина
называется чистотой состояния (quantum state purity).
Энтропия#
Энтропия фон Неймана – это другая численная характеристика того, насколько сильно наша система смешанная. Ее выражение очень похоже на выражение для классической энтропии Шеннона. Только в отличие от классики, в квантовой механике мы имеем матрицу плотности, поэтому в выражении у нас фигурирует матричный логарифм:
Спектральная декомпозиция матрицы плотности#
Определение матрицы плотности (1) представляет собой сумму матриц плотностей чистых состояний, взятых с некоторыми вероятностями. Интересно, что совершенно разным комбинациям чистых состояний могут соответствовать одинаковые матрицы плотности. Например, состояние кубита, который с вероятностью 50% находится в состоянии \(\ket{0}\) и с вероятностью 50% в состоянии \(\ket{1}\) совершенно неотличимо от такой же равновероятной смеси состояний \(\ket{+}\) и \(\ket{-}\):
Соотношение (1) также можно рассматривать как спектральную декомпозицию матрицы плотности. В этом случае состояния \(\Psi_n\) образуют ортонормированный базис, а вероятности \(p_n\) – это собственные значения \(\rho\). Как чистота (3), так и энтропия (4) зависят лишь от этих собственных значений.
Смешанные состояния и запутанность#
Рассмотрим ситуацию, когда описываемую квантовую систему \(\Phi\) можно разделить на две подсистемы, \(\phi\) и \(\psi\), и состояние этой системы \(\ket{\Phi}\) является суперпозицией состояний двух подсистем:
Здесь два ортонормированных набора векторов состояния \(\ket{\phi_i}\) и \(\ket{\psi_j}\) описывают две части всей системы. Для такого состояния не всегда можно сказать, в каком именно состоянии находится каждая подсистема.
Note
Вспомним обсуждение кота Шредингера в лекции про кубит – упрощая до предела, можно считать, что радиоактивный атом является одной системой, а несчастный кот – второй.
До измерения ни атом, ни кот не имеют определенного состояния, а находятся в суперпозиции возможных состояний.
Что же мы можем сделать, если у нас есть доступ лишь к одной из двух подсистем, а измерить состояние второй мы уже не можем? В таком случае, все наши наблюдаемые величины будут отвечать операторами \(A_\psi\), которые действует только на вторую подсистему. В примере кота Шредингера можно допустить, что экспериментально пронаблюдать мы можем лишь состояние кота, а состояние радиоактивного атома недоступно нам для измерения. В таком случае состояние второй подсистемы можно полностью описать используя редуцированную матрицу плотности. Редуцированная матрица плотности получается из матрицы плотности чистого состояния всей системы суммированием по вероятностям различных состояний первой подсистемы:
где
а \(\operatorname{Tr}_\phi\) означает частичный след по второй подсистеме, звездочка – комплексное сопряжение. В таких обозначениях значение для среднего от оператора \(A\) вычисляется по формуле
Здесь след матрицы уже вычисляется по первой подсистеме.
Чаще всего при обсуждении смешанных состояний рассматривают только одну “подсистему”, считая, что вторая – это некоторый макроскопический объект (“резервуар”, например лаборатория или даже вся Вселенная). В этом случае определение матрицы плотности (1) можно рассматривать как редуцированную матрицу плотности (5), из которой убрали нерелевантные и неконтролируемые степени свободы.
Запутанные и сепарабельные состояния#
Давайте вернемся к представлению состояния составной системы и зададимся вопросом: что можно сказать о связи между частями системы с точки зрения квантового описания? Для системы из двух кубитов такая составная система в общем случае может быть записана в явном виде (в этом разделе мы в основном следуем изложению из книги [01]):
где индексы \(A\) и \(B\) здесь обозначают первый и второй кубиты, соответственно, а условие нормировки дает
Теперь, как можно показать, состояние типа (6) может быть представлено в виде произведения состояний двух отдельных кубитов, если \(ad = dc\):
где для выражения (6)
В других случаях, когда \(ad \neq dc\), состояние составной системы не представимо в виде произведения состояний подсистем, такие состояния называют несепарабельными (nonseparable). Другими словами, результат измерения состояния подсистемы \(A\) будет зависеть от состояния подсистемы \(B\). Это означает, что для квантовых систем возможна нелокальная корреляция. Такое свойство квантовых систем называется запутыванием (entanglement), а сами состояния запутанными (entangled).
Note
В отличие от анлийского языка, в русском языке не сложилось единой терминологии в отношении запутанных состояний. На момент написания этой лекции (осень 2021 года) в статье Квантовая запутанность русскоязычной Википедии указывается восемь (!) отличающихся терминов для этого явления, например, “запутанность”, “перепутанность” или “сцепленность”. Сделать с этим что-то сложно, остается только иметь в виду имеющиеся обстоятельства. Мы будем стараться употреблять термин запутанность и, соответственно, запутанные состояния.
Приведем пару примеров запутанных состояний:
\(b = c = 0, a = d = \pm 1/\sqrt{2}\) – состояние “шредингеровского кота”, см. [01] и [07], такая формула для вектора состояния возникает для суперпозиции двух макроскопически различимых состояний одной из подсистем, например, живой или мертвый кот.
\(a = d = 0, b = -c = \pm 1/\sqrt{2}\) – такое состояние называется ЭПР-парой (EPR, от Einstein-Podolsky-Rosen) и это очень важный пример из истории изучения запутанности в квантовой физике.
Note
в 1930-е происходили многочисленные споры об “интерпретации” (сути) квантовой механики. Именно тогда Эйнштейн, Шредингер и их коллеги обратили внимание на несепарабельные состояния и затем Эйнштейном, Подольским и Розеном был сформулирован “парадокс” – что квантовая механика либо нелокальна (т.е. несовместима с теорией относительности), либо неполна (мы учитываем не все параметры при описании состяния квантовых систем). Именно с дискуссией о сути запутанности связана знаменитая цитата Эйнштейна “Бог не играет в кости” и менее известный ответ Нильса Бора, “Альберт, не указывай Богу, что ему делать.”
Довольно долго изучение запутанности и связанных с ней трудностей считались сложным, но не основными вопросами квантовой физики. Но с развитием квантовой информатики стало понятно, что без запутанности нельзя разрабатывать квантовые компьютеры и системы квантовой связи. В настоящее время существуют устоявшиеся методы создания запутанных состояний в эксперименте. А для целей нашего курса, в симуляциях, достаточно использовать двухкубитные гейты, которые обсуждались в предыдущей лекции, например CNOT или CZ, который используется в лекции про Градиенты квантовых схем.
В качестве примера давайте посмотрим, как можно создать запутанное состояние в PennyLane. Начнем с импортов и создания двухкубитной схемы:
import pennylane as qml
from pennylane import numpy as np
dev = qml.device("default.qubit", wires=2)
/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
warnings.warn("Setuptools is replacing distutils.")
Далее применим к первому кубиту операцию поворота \(\hat{RX}\), запутаем кубиты с помощью \(\hat{CNOT}\) и далее оценим запутанность с помощью измерения оператора Паули \(\hat{\sigma^z}\):
@qml.qnode(dev)
def circuit(param):
qml.RX(param, wires=0)
qml.CNOT(wires=[0, 1])
return qml.expval(qml.PauliZ(0)), qml.expval(qml.PauliZ(1))
В этом примере значение переменной param определяет степень запутанности, и для \(\pi/2\) запутанности будет максимальна. В результате оба кубита будут максимально смешанными и средний результат измерения будет нулевым:
print(circuit(np.pi / 2))
[2.22044605e-16 2.22044605e-16]
(код взят из официальной демонстрации для библиотеки PennyLane)
Разложение Шмидта#
В этом разделе мы познакомимся с важной процедурой – разложением Шмидта, которое тесно связано со спектром редуцированных матриц плотности состояния составной квантовой системы и благодаря которому легко увидеть, является ли состояние системы запутанным или нет.
Снова запишем чистое двухчастичное состояние \(\ket{\Phi}\) квантовой системы, в пространстве \(H_{\phi} \otimes H_{\psi}\) двух подсистем \(\phi\) и \(\psi\). Покажем тогда, что существуют ортонормированные состояния \(\ket{i_{\phi}}\) системы \(\phi\) и ортонормированные состояния \(\ket{i_{\psi}}\) системы \(\psi\), которые дадут нам разложение:
где \(\lambda_i\) – неотрицательные числа (коэффициенты Шмидта), удовлетворяющие условию \(\sum_{i} \lambda_{i}^{2} = 1\).
Для доказательства рассмотрим случай, когда обе подсистемы имеют пространство одинаковой размерности. Пусть тогда \(\ket{n}\) и \(\ket{k}\) состояния образуют произвольный ортонормированный базис для подсистем \(\phi\) и \(\psi\). Соответственно, тогда состояние системы \(\ket{\Phi}\) может быть представлено в виде разложения:
Константы разложения \(a_{nk}\) образуют эрмитово-сопряженную комплексную матрицу \(A\), которую можно привести к диагональному виду. Для этого применим к этой матрице сингулярное разложение (или SVD-разложение) вида: \(A=U \cdot S \cdot V^{*}\), где \(U\) и \(V\) – унитарные матрицы, а \(S\) – диагональная матрица с неотрицательными действительными числами на диагонали (эти числа называют сингулярными числами матрицы \(A\), и их набор однозначно определяется матрицей). Тогда разложение (8) можно привести к виду:
Теперь переопределим базис состояний в подсистемах \(\phi\) и \(\psi\):
и обозначим \(s_{ii} \equiv \lambda_{i}\). В результате разложение (9) преобразуется к виду:
В силу унитарности \(U\) и \(V\) наборы базисных состояний \(\ket{i_{\phi}}\) и \(\ket{i_{\psi}}\) в (10) образуют полную ортонормированную систему, или базис Шмидта, а само представление (7) называют разложением Шмидта. Число ненулевых значений коэффициентов Шмидта \(\lambda_i\) называется числом (или рангом \(rank(A)=dim{s_{ii} : s_{ii} > 0}\)) Шмидта для состояния \(\ket{\Phi}\). В теории мер квантовой запутанности это число характеризует степень (или меру) запутанности состояний сложной системы. Чистое двухчастичное состояние запутанно тогда и только тогда, когда его число Шмидта \(> 1\), и чем больше число Шмидта, тем сильнее запутано состояние.
Следствием приведенных выше свойств является важная связь между коэффициентами Шмидта чистого запутанного состояния со спектром его редуцированных матриц плотности \(\rho_{\phi} = \mbox{Tr}_{\psi} \left( \ket{\Phi}\bra{\Phi}\right)\) и \(\rho_{\psi} = \mbox{Tr}_{\phi} \left( \ket{\Phi}\bra{\Phi}\right)\). Несложно убедиться, что собственные значения редуцированных матриц \(\rho_{\phi}\) и \(\rho_{\psi}\) совпадают и представляют собой квадраты коэффициентов Шмидта, а их собственные вектора представляют собой состояния \(\ket{i_{\phi}}\) и \(\ket{i_{\psi}}\) соответственно. Эти свойства дают нам удобный алгоритм вычисления разложения Шмидта двухчастичного состояния \(\ket{\Phi}\) через редуцированные матрицы его подсистем: (1) на первом этапе следует вычислить редуцированные матрицы плотности \(\rho_{\phi}\) и \(\rho_{\psi}\); (2) на втором этапе найти общие собственные значения \(a_i\) и соответствующие им собственные векторы \(\ket{i_{\phi}}\) и \(\ket{i_{\psi}}\) для матриц \(\rho_{\phi}\) и \(\rho_{\psi}\); (3) записать разложение Шмидта в виде:
Описания эволюции смешанного состояния#
Квантовая динамика#
Напомним, что квантовая динамика в терминах волновых функций \(\ket{\Psi}\) описывается при помощи уравнения Шредингера:
Аналогичное уравнение можно получить и для матриц плотности. Оно называется уравнением фон Неймана и записывается через коммутатор \([]\), который определен как \([\hat{A}, \hat{B}] = \hat{A}\hat{B} - \hat{B}\hat{A}\):
Аналогично, если действие каких-то унитарных операций изменяет вектор состояния \(\ket{\Psi}\) на \(\hat{U} \ket{\Psi}\), то матрицу плотности оно должно изменять как
Важное свойство унитарных матриц – их собственные значения по модулю равны единице. Действие унитарного оператора не изменяет собственных значений матрицы плотности, но вращает собственный ее базис. Исходя из этого можно сделать вывод о том, что ни чистота, ни энтропия не могут изменяться в результате унитарных операций.
Измерения и томография#
Квантовая механика работает так, что любое измерение приводит к коллапсу волновой функции и является необратимым. А еще измерения, например, состояния \(\ket{+}\) и \(\ket{-}\) не различимы при измерениях по оси \(\mathbf{Z}\) – для обоих состояний мы будем получать \(\ket{1}\) и \(\ket{0}\) с вероятностью \(0.5\), то есть нам нужно измерять по всем базисам. В общем, получается, что восстановить амплитуду и фазу волновой функции \(\Psi\) это большая проблема, если добавить сюда вероятностный характер измерения.
Note
Строго говоря это не просто “большая” проблема, а настоящая NP-полная задача оптимизации!
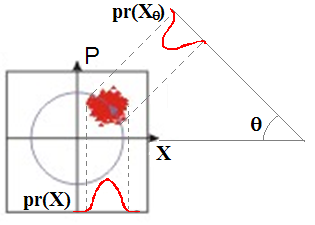
Fig. 26 Иллюстрация фазовой проблемы.#
Эта задача обычно решается при помощи квантовой томографии, и восстанавливают как раз не волновую функцию \(\Psi\), а матрицу плотности \(\rho\) (потому что в реальных экспериментах и задачах почти не бывает чистых состояний). Представим, что наша квантовая система описывается базисом \(y_i\) – набором из \(2^N\) векторов, причем каждому из этих базисных векторов соответствует свое собственное значение – результат измерения (подробнее об этом было в лекции про кубит). Тогда если у нас будет достаточно много результатов измерений, то мы сможем восстановить нашу матрицу плотности \(\rho\) методом максимизации правдоподобия. Выражение для правдоподобия в этом случае можно записать как:
где \(q_i\) – это частота получения собственного значения, соответствующего волновой функции \(\ket{y_i}\) (потому что измерение переводит наше состояние в базисный вектор, соответствующий результату измерения). В итоге увеличивая число измерений мы приближаем частоты \(q_i\) к вероятностям \(\bra{\Psi}(\ket{y_i}\bra{y_i})\ket{\Psi}\), а нашу матрицу \(\rho\) к ее истинному виду.
Методы квантовой томографии являются критической частью, в том числе, квантовой связи, так как системы там обычно небольшие, но восстанавливать надо всю матрицу плотности.
Что мы узнали?#
Формализм матрицы плотности позволяет описывать составные системы (например, один кубит в многокубитной системе)
Чаще всего в реальных экспериментах у нас ситуация “мы приготовили состояние, но точно не знаем какое” и волновая функция нам не подходит
Что такое квантовая запутанность и как ее можно описать
Состояние части запутанного состояния – смешанное
Отличие смешанного состояния от чистого можно охарактеризовать параметром типа энтропии