Quantum K-nearest neighbor

Автор(ы):

• Токарев Игорь

Введение

Если вы занимались машинным обучением, то, скорее всего, знакомы с классическим алгоритмом $k$ ближайших соседей. Он относительно прост, применяется как в задачах классификации, так и в регрессии. Кстати, классический knn можно вспомнить обратившись к лекции от ODS по классическому машинному обучению.

Давайте немножко вспомним задачу классификации с использованием классического $kNN$ алгоритма:

У нас есть $\overrightarrow{x}\in \{0,1{\}}^N$ – тестовый образец, а также тренировочные образцы – это набор векторов $\overrightarrow{v_i}\in \{0,1{\}}^N$, в котором каждый вектор уже размечен. И наша задача подобрать правильную метку тестовому образцу.

Тогда мы пройдём следующие шаги:

1. Вычислим похожесть между тестовым образцом и каждым тренировочным образцом.

2. Найдем $k$ ближайших к тестовому образцу соседей.

3. Подсчитаем количество представителей для каждого класса и приписываем метку самого часто встречающегося класса к тестовому образцу.

Самой трудозатратным шагом является вычисление расстояния от тестового образца к каждому тренировочному. Также и в квантовой версии алгоритма.

Note

На текущий момент разработано несколько разных версий квантового алгоритма поиска ближайших соседей. Есть версия основанная расстоянии Хэмминга [LTG21]:

Расстояние Хэмминга между векторами $\overrightarrow{x}$ и $\overrightarrow{v_i}$:

$$d_i=|\overrightarrow{x}-\overrightarrow{v_i}|=\sum _{j=1}^N(x_j\oplus v_{ij})$$

Но в данной работе мы обратим внимание на версию, которая вычисляет fidelity между двумя векторами состояниями.

Пусть задано Гильбертово пространство $n$ кубитов, размерности $N=2^n$. Вектор $|\psi ⟩\in H$ – это тестовое состояние, для которого нам нужно определить метку.

Пусть $\{|\varphi ⟩:j\in \{0,...,M-1\}\}\subset H$ - это набор тренировочных состояний, для которых мы знаем их метки. $M=2^m,m\in \mathbb{Z}$

Определим fidelity между тестовым состоянием и $j$-тым тренировочным $|{\varphi }_j⟩$ как

$$F_j=F(\psi ,{\varphi }_j)=|⟨\psi |{\varphi }_j⟩{|}^2$$

В свою очередь $F=[F_0,F_1,...,F_{M-1}]$ - это таблица fidelity значений между тестовым состоянием и каждым из тренировочных.

Заметим, что задача нахождения $k$ ближайших соседей сводится к задаче нахождения $k$ максимумов значений fidelity из таблицы $F$. Для этого мы должны реализовать оракула

$$O_{y,A}|j⟩|0⟩=|j⟩|f_{y,A}(j)⟩,$$

где $f_{y,A}$ - это булева функция определённая как

$$\begin{array}{r}{f}_{y,A}(j)=\{\begin{array}{l}1:F_j>F_y\text{ and }j\notin A,\\ 0:\text{ otherwise },\end{array}\end{array}$$

Алгоритм

Далее мы алгоритм представленный в работе [BAG21].

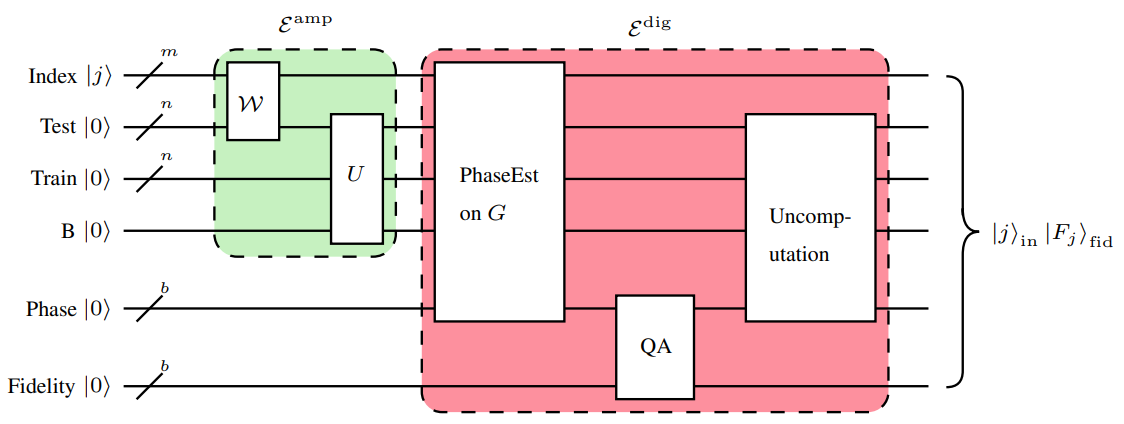
Fig. 67 Принципиальная схема QkNN алгоритма. Взято из работы [BAG21].

Квантовый алгоритм поиска $k$ ближайших соседей будет состоять из двух основных шагов:

1. Используй оракул $O_{y,A}$ (для алгоритма Гровера) мы находим $k$ состояний $\{|{\varphi }_{j1}⟩,...,|{\varphi }_{jk}⟩\}$ для которых значение fidelity с тестовым состоянием максимально.

2. Найти преобладающую метку среди $k$ найденных состояний и присвоить её тестовому состоянию.

Самой нетривиальной задачей для нас будет построение оракула $O_{y,A}$.

1. Вначале нужно составить оператор $\mathcal{F}$, который выполняет преобразование вида:

   $$\mathcal{F}|j⟩|0⟩=|j⟩|F_j⟩$$

   для $j\in \{0,...,M-1\}$. $|F_j⟩$ – это одно из базисных состояний вычислительного базиса (выражающее двоичное представление числа $F_j$).

   • Выполняется преобразование: ${\xi }^{amp}|j⟩|0⟩=|j⟩|{\psi }_j⟩$. В амплитуду состояния $|{\psi }_j⟩$ закодирована информация о числе $F_j$ Делается это с помощью Swap test.

     Swap test это применение контролируемой операции $Swap$, которым можно пользоваться для того, чтобы статистически определять fidelity: $F(\psi ,\varphi )=|⟨\psi |\varphi ⟩{|}^2$ между двумя произвольными чистыми состояниями $|\psi ⟩$ и $|\varphi ⟩$.

     $$\begin{array}{r}CSWAP(|0⟩|\psi ⟩|\varphi ⟩)=|0⟩|\psi ⟩|\varphi ⟩\\ CSWAP(|1⟩|\psi ⟩|\varphi ⟩)=|1⟩|\psi ⟩|\varphi ⟩\end{array}$$

     

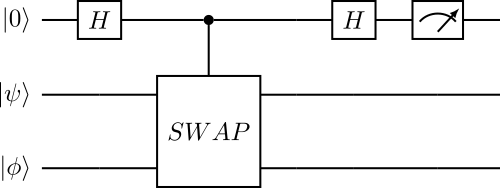
     Fig. 68 Схема Swap test

   • Выполняется преобразование ${\xi }^{dig}|j⟩|{\psi }_j⟩=|j⟩|F_j⟩$

     И тогда $\mathcal{F}={\xi }^{dig}{\xi }^{amp}$.

2. Берём 2 пары регистров $i_1,f_1;i_2,f_2$. Инициализируются они в форме $|j{⟩}_{i_1}|0{⟩}_{f_1}|y{⟩}_{i_2}|0{⟩}_{f_2}$

   Применяется $\mathcal{F}$ на каждой паре:

   $$\mathcal{F}(|j{⟩}_{i_1}|0{⟩}_{f_1})\mathcal{F}(|y{⟩}_{i_2}|0{⟩}_{f_2})=|j{⟩}_{i_1}|F_j{⟩}_{f_1}|y{⟩}_{i_2}|F_y{⟩}_{f_2}$$

3. Теперь информация закодирована в регистры и нам нужно реализовать функцию $f_{y,A}$. И пусть $\mathcal{C}$ это оператор, реализующий $f_{y,A}$.

   $$\mathcal{C}(|j{⟩}_{i_1}|F_j{⟩}_{f_1}|y{⟩}_{i_2}|F_y{⟩}_{f_2})=|j{⟩}_{i_1}|0{⟩}_{f_1}|f_{y,A}{⟩}_{i_2}|0{⟩}_{f_2}$$

Теперь займёмся вопросом конструирования оракула $O_{y,A}$. Просьба держаться за ваши кресла.

Вначале мы подготовим состояния. Но чтобы это сделать нам нужны оракулы $\mathcal{V},\mathcal{W}$. Как их имплементировать указано в статье, которая указывалась выше.

$$\mathcal{V}|0^n⟩=|\psi ⟩$$

$$\mathcal{W}|j⟩|0^n⟩=|j⟩|\varphi ⟩$$

для всех $j\in \{0,...,M-1\}$.

1. Инициализируем 4 регистра $i$, $tr$, $tst$, $B$ с соответствующим количеством кубитов в каждом $m$, $n$, $n$, $1$, где $n=\log (N)$, $m=\log (M)$.

   $$|j{⟩}_i|0^{\otimes n}{⟩}_{tr}|0^{\otimes n}{⟩}_{tst}|0{⟩}_B$$

2. Применяем $\mathcal{W}$

   $$\mathcal{W}(|j{⟩}_i|0^{\otimes n}{⟩}_{tr}|0^{\otimes n}{⟩}_{tst}|0{⟩}_B)=|j{⟩}_i|{\varphi }_j{⟩}_{tr}|0^{\otimes n}{⟩}_{tst}|0{⟩}_B$$

3. Применяем $\mathcal{V}$

   $$\mathcal{V}(|j{⟩}_i|{\varphi }_j{⟩}_{tr}|0^{\otimes n}{⟩}_{tst}|0{⟩}_B)=|j{⟩}_i|{\varphi }_j{⟩}_{tr}|{\psi }_j{⟩}_{tst}|0{⟩}_B$$

4. Применяем swap test между тренировочным регистром $tr$ и тестовым регистром $tst$, а регистр $B$ будет выступать в качестве контрольного.

   $$\frac{1}{2}[(|{\varphi }_j⟩|\psi {⟩}_{tst}+|{\psi }_j⟩|\varphi {⟩}_{tst})|0{⟩}_B+(|{\varphi }_j⟩|\psi {⟩}_{tst}-|{\psi }_j⟩|\varphi {⟩}_{tst})|1{⟩}_B]=|j{⟩}_i|{\psi }_j{⟩}_{tr,tst,B}$$

   Определим $U$ как унитарное преобразование, которое объединяет шаги 3-4. Кстати, если мы сейчас произведём измерение регистра $B$, то будем иметь

   $$\begin{array}{r}Pr(B=0)=\frac{1+F_j}{2}\\ Pr(B=1)=\frac{1-F_j}{2}\end{array}$$

   На этом шаге информация о $fidelity$ теперь закодирована в амплитуды. Теперь же мы должны перевести $fidelity$ из амплитуды в число.

5. Теперь мы будем конструировать новый гейт G. Вообще говоря, он описан в работе [MKF19], где вы можете подробнее с ним ознакомиться.

   $$G=U_{tr,tst,B}{\mathcal{W}}_{i,tr}{S}_{0_{tr,tst,B}}{\mathcal{W}}_{i,tr}^{†}{U}_{tr,tst,B}^{†}{Z}_B,$$

   где $Z_B$ – это действие гейта $Z$ на регистре $B$, $S_0=I-2|0⟩⟨0|$.

6. Текущее состояние $|\psi {⟩}_{tr,tst,B}$ может быть представлено в виде композиции двух состояний

   $$|{\psi }_j⟩=\frac{-i}{\sqrt{2}}(e^{i\pi {\theta }_j}|{\psi }_{j+}⟩-e^{-i\pi {\theta }_j}|{\psi }_{j-}⟩)$$

7. Теперь применяем алгоритм QPE (Quantum Phase Estimation), чтобы перевести значение фазы ${\theta }_j$ в числовое представление.

   $$QPE(|{\psi }_j⟩)=\frac{-i}{\sqrt{2}}|j{⟩}_i[e^{i\pi {\theta }_j}|{\theta }_j{⟩}_{ph}|{\psi }_{j+}{⟩}_{tr,tst,B}-e^{-i\pi {\theta }_j}|1-{\theta }_j{⟩}_{ph}|{\psi }_{j-}{⟩}_{tr,tst,B}]=|j{⟩}_i|{\psi }_{j,AE}{⟩}_{ph,tr,tst,B}$$

8. Применяем алгоритм квантовой арифметики:

   $$|j⟩|F_j{⟩}_{fid}|{\psi }_{j,AE}{⟩}_{ph,tr,tst,B}$$

9. Обнуляем регистры $ph,tr,tst,B$ и получаем $|j{⟩}_i|F_j{⟩}_{fid}$ На самом деле шаги 5-9 составляют оператор ${\xi }^{dig}$, который мы упоминали ранее.

10. Теперь применяем оператор $\mathcal{F}$

    $$|j{⟩}_{i1}|F_j{⟩}_{f1}|y{⟩}_{i2}|F_y{⟩}_{f2}$$

11. Добавим кубит $Q_1$ для выполнения сравнения

    $$\begin{array}{r}J|a⟩|b⟩|0⟩=\{\begin{array}{l}|a⟩|b⟩|1⟩:a>b,\\ |a⟩|b⟩|0⟩:a\le b,\end{array}\end{array}$$
    $$|j{⟩}_{i1}|F_j{⟩}_{f1}|y{⟩}_{i2}|F_y{⟩}_{f2}|g(j){⟩}_{Q_1},$$

    где

    $$\begin{array}{r}g(j)=\{\begin{array}{l}1:F_j>F_y,\\ 0:F_j\le F_y,\end{array}\end{array}$$

    По кубиту $Q_1$ мы сможем распознать все индексы $j$ для которых $F_j>F_y$.

12. Обнуляем регистры $i2$, $f2$.

13. Добавляем ещё один кубит $Q_2$ для каждого $i_l\in A$, применяя гейт $D^{(i_l)}$

    $$\begin{array}{r}{D}^{(i_l)}|j⟩|0⟩=\{\begin{array}{l}|j⟩|1⟩:j=i_l,\\ |j⟩|0⟩:j\ne i_l,\end{array}\end{array}$$

    на индексах регистра. И в результате получим состояние

    $$|j{⟩}_{i1}|F_j{⟩}_{f1}|g(j){⟩}_{Q_1}|{\chi }_A(j){⟩}_{Q_2}$$

14. О да… Теперь мы добавляем ещё один кубит $Q_3$. Применяем гейт $X$ на кубите $Q_2$ и гейт Тоффоли с контролирующими $(Q_1,Q_2)$ и целевой $Q_3$

    $$|j{⟩}_{i1}|F_j{⟩}_{f1}|g(j){⟩}_{Q_1}|{\chi }_A(j){⟩}_{Q_2}|f_{y,A}(j){⟩}_{Q_3}$$

15. Обнуляем все регистры, кроме $Q_3$

    $$|j{⟩}_{i1}|f_{y,A}(j){⟩}_{Q_3}$$

    Что ж, вот мы и построили преобразование $O_{y,A}$ которое так хотели

    $$O_{y,A}|j⟩|0⟩=|j⟩|f_{y,A}(j)⟩$$