Классический SVM
Contents
Классический SVM#
Автор(ы):
Описание лекции#
В этой лекции мы рассмотрим классический метод опорных векторов (SVM) и разберем стоящую за ним математику. С согласия Евгения Соколова, мы во многом переиспользуем конспекты лекций курса “Машинное обучение”, читаемого на ФКН ВШЭ.
План лекции такой:
линейная классификация;
интуиция метода опорных векторов;
метод опорных векторов для линейно-разделимой выборки;
метод опорных векторов для линейно-неразделимой выборки;
решение задачи метода опорных векторов;
ядерный переход;
плюсы и минусы SVM.
Линейная классификация#
Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на два полупространства, в каждом из которых прогнозируется одно из двух значений целевого класса. Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.
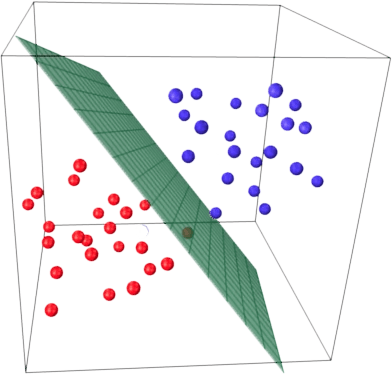
Fig. 71 Линейная классификация#
Рассмотрим задачу бинарной классификации, в которой
Линейная модель классификации определяется следующим образом:
где
Note
Хорошо бы для векторов ставить стрелку и писать
Часто считают, что среди признаков
есть константа,
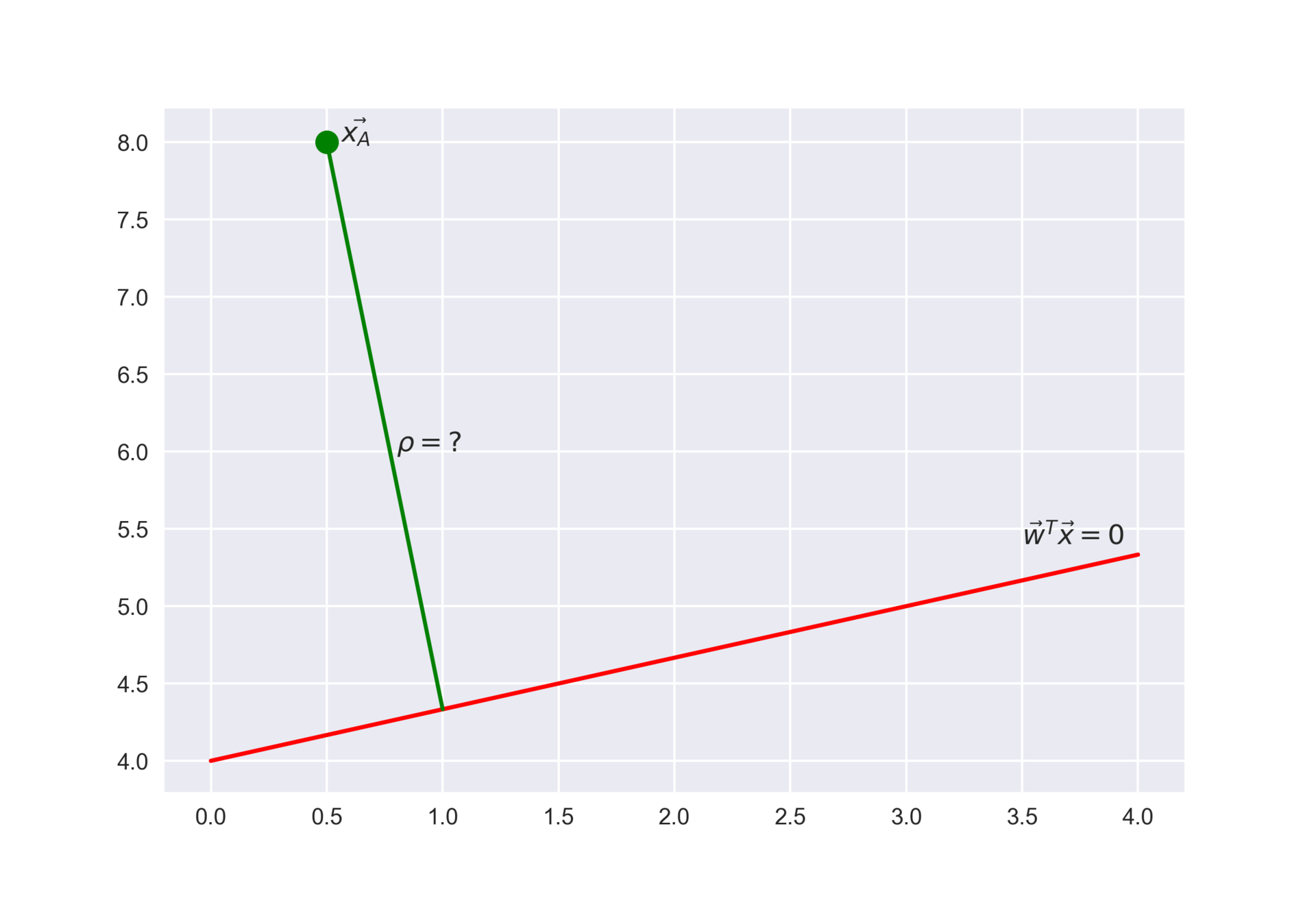
Fig. 72 Расстояние от точки до плоскости#
Геометрически линейный классификатор соответствует гиперплоскости с вектором нормали
Упражнение на метод Лагранжа
Метод Лагранжа – очень важный метод оптимизации функций при наличии органичений. Этот же метод вовсю используется ниже в методе опорных векторов.
Рекомендуется ознакомиться с методом Лагранжа и решить (ручками!) простую оптимизационную задачу вида
А мы выведем указанную выше формулу расстояния от точки до плоскости. Вообще это можно сделать разными способами – алгебраически и геометрически. Но давайте посмотрим на эту задачу (внезапно) как на задачу оптимизации и решим ее методом Лагранжа. Это послужит неплохой тренировкой перед тем как окунуться в SVM.
Итак, представим задачу в таком виде: хотим найти точку
Лагранжиан:
Далее надо приравнять нулю частные производные лагранжиана по его аргументам. Из
Теперь домножим это уравнение скалярно на
Тогда наконец
Таким образом, линейный классификатор разделяет пространство на две части с помощью гиперплоскости, и при этом одно полупространство относит к положительному классу, а другое – к отрицательному.
Пожалуй, самый известный и популярный на практике представитель семейства линейных классификаторов – логистическая регрессия. На русском языке про нее можно почитать в статье открытого курса по машинному обучению или в упомянутых лекциях Евгения Соколова. В этих лекциях также объясняется, как происходит обучение модели (подбор весов
Отступ классификации#
Оказывается полезным рассмотреть выражение
Это отступ классификации (margin) для объекта обучающей выборки
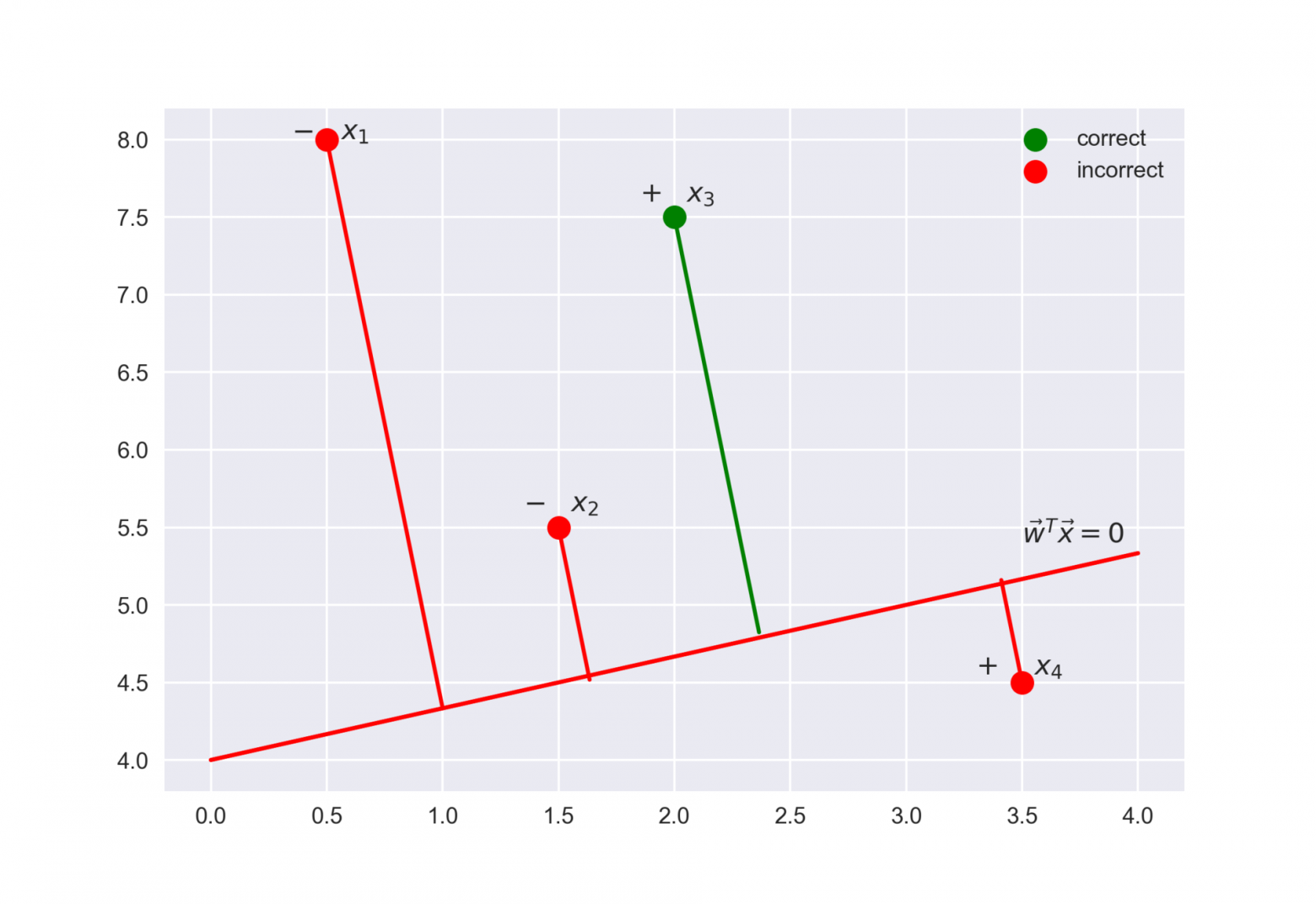
Fig. 73 Иллюстрация к понятию отступа классификации#
Отступ – это своего рода “уверенность” модели в классификации объекта
если отступ большой (по модулю) и положительный, это значит, что метка класса поставлена правильно, а объект находится далеко от разделяющей гиперплоскости (такой объект классифицируется уверенно). На рисунке –
если отступ большой (по модулю) и отрицательный, значит метка класса поставлена неправильно, а объект находится далеко от разделяющей гиперплоскости (скорее всего такой объект – аномалия, например, его метка в обучающей выборке поставлена неправильно). На рисунке –
если отступ малый (по модулю), то объект находится близко к разделяющей гиперплоскости, а знак отступа определяет, правильно ли объект классифицирован. На рисунке –
Далее увидим, что понятие отступа классификации – часть функции потерь, которая оптимизируется в методе опорных векторов.
Интуиция метода опорных векторов#
Метод опорных векторов (Support Vector Machine, SVM) основан на идее максимизации зазора между классами. Пока не вводим этот термин формально, но передадим интуицию метода. На Рис. Fig. 74 показана линейно-разделимая выборка, кружки соответствуют положительным примерам, а квадраты – отрицательным (или наоборот), а оси – некоторым признакам этих примеров. На рисунке слева показаны две прямые (в общем случае – гиперплоскости), разделяющие выборку. Кажется, что синяя прямая лучше тем, что она дальше отстоит от примеров обучающей выборки, чем красная прямая (зазор – больше), и потому лучше будет разделять другие примеры из того же распределения, что и примеры обучающей выборки. То есть такой линейный классификатор будет лучше обобщаться на новые данные. Теория подтверждает описанную интуицию [MRT18].
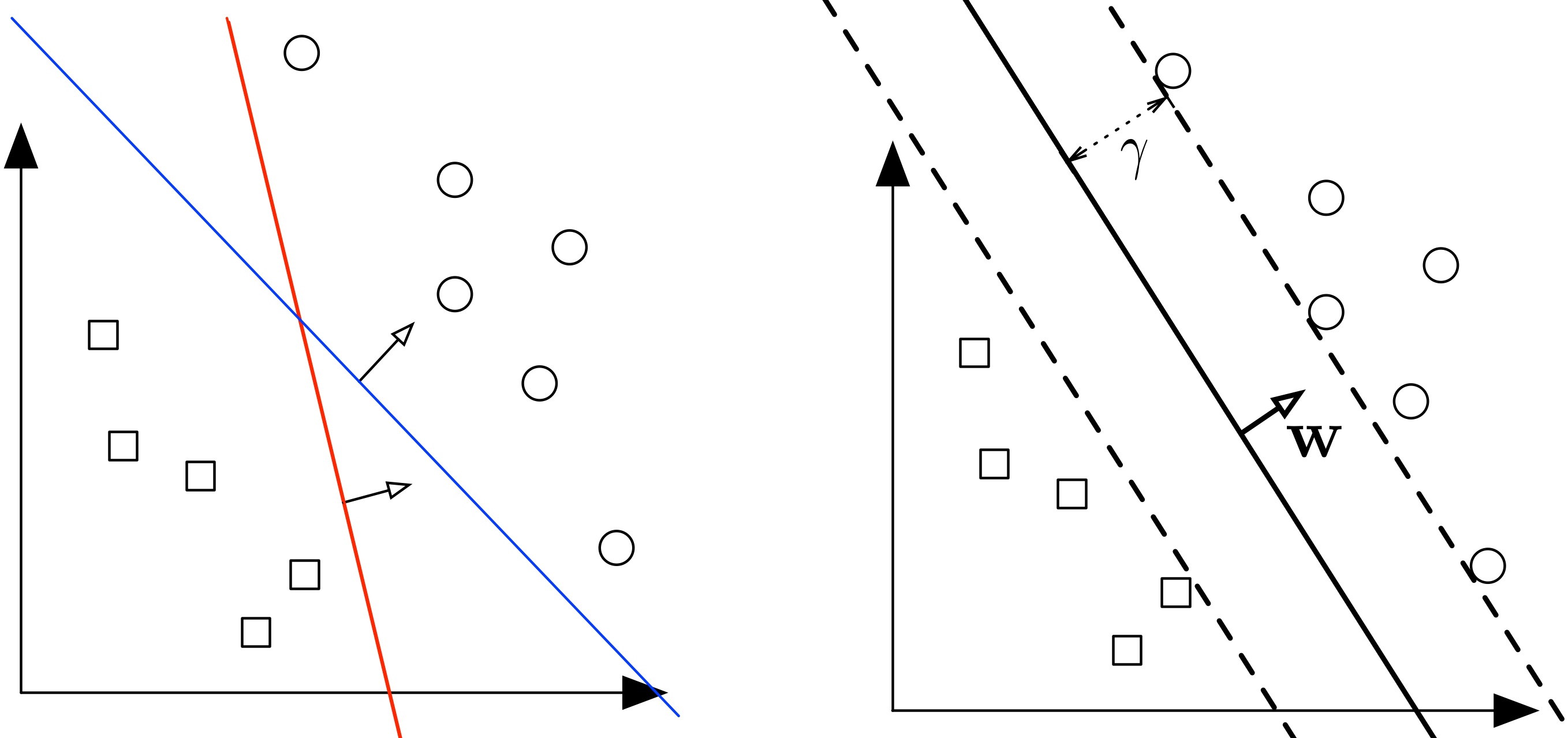
Fig. 74 Слева показаны две прямые (в общем случае – гиперплоскости), разделяющие выборку. Справа показана прямая, максимизирующая зазор между классами. Источник: лекция Cornell#
Note
Одним из ключевых авторов алгоритма SVM является Владимир Вапник – советский и американский (с 1991-го года) ученый, который также сделал огромный вклад в теорию классического машинного обучения. Его имя носит одно из ключевых теоретических понятий машинного обучения – размерность Вапника-Червоненкиса.
Метод опорных векторов для линейно-разделимой выборки#
Будем рассматривать линейные классификаторы вида
Заметьте, что мы вернули сдвиг (bias)
Заметим, что если одновременно умножить параметры
Как мы увидели выше, расстояние от произвольной точки
Тогда расстояние от гиперплоскости до ближайшего примера из обучающей выборки равно
Данная величина также называется зазором (margin). Опять же, эту величину очень легко перепутать с отступом классификации, про который мы говорили выше и который тоже margin в англоязычном варианте. Заметим, что отступ – функция параметров
Таким образом, если классификатор без ошибок разделяет обучающую выборку, то ширина его разделяющей полосы равна
Итак, требуется построить классификатор, идеально разделяющий обучающую выборку, и при этом имеющий максимальный отступ.
Запишем соответствующую оптимизационную задачу, которая и будет определять метод опорных векторов для линейно разделимой выборки (hard margin support vector machine):
Здесь мы воспользовались тем, что линейный классификатор дает правильный ответ на примере
В данной задаче функционал является строго выпуклым, а ограничения линейными, поэтому сама задача является выпуклой и имеет единственное решение. Более того, задача является квадратичной и может быть решена крайне эффективно.
Метод опорных векторов для линейно-неразделимой выборки#
Рассмотрим теперь общий случай, когда выборку
невозможно идеально разделить гиперплоскостью.
Это означает, что какие бы
Сделаем эти ограничения мягкими, введя штраф
Отметим, что если отступ объекта лежит между нулем и
единицей (
Величина
Эти две задачи противоречат друг другу: как правило, излишняя подгонка под выборку приводит к маленькому зазору, и наоборот – максимизация зазора приводит к большой ошибке на обучении. В качестве компромисса будем минимизировать взвешенную сумму двух указанных величин.
Приходим к оптимизационной задаче, соответствующей методу опорных векторов для линейно неразделимой выборки (soft margin support vector machine):
Чем больше здесь параметр
Сведение к безусловной задаче оптимизации#
Покажем, что задачу метода опорных векторов можно свести к задаче безусловной оптимизации функционала, который имеет вид верхней оценки на долю неправильных ответов.
Перепишем условия задачи:
Поскольку при этом в функционале требуется, чтобы штрафы
Данное выражение для
Эта задача является негладкой, поэтому решать её может быть достаточно тяжело. Тем не менее, она показывает, что метод опорных векторов, по сути, как и логистическая регрессия, строит верхнюю оценку на долю ошибок и добавляет к ней стандартную квадратичную регуляризацию. Только если в случае логистической регрессии этой верхней оценкой была логистическая функция потерь (опять сделаем отсылку к статье из открытого курса машинного обучения), то в случае метода опорных векторов это функция вида
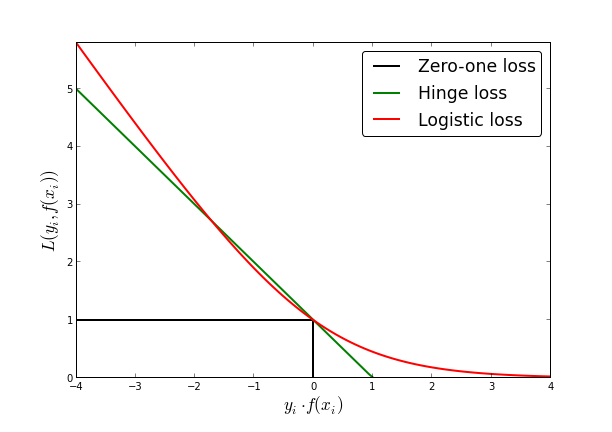
Fig. 75 Пороговая, кусочно-линейная и логистическая функции потерь#
Это становится понятнее в терминах упомянутого выше отступа
Note
Бытует мнение, что метод опорных векторов сегодня нигде не используется из-за его сложности (как минимум квадратичной по числу примеров). Однако, это не так. Линейный SVM вполне неплохо можно применять в задачах с высокой размерностью объектов обучающей выборки, например, для классификации текстов с Tf-Idf или любым другим разреженным представлением. В частности, Vowpal Wabbit – очень эффективная утилита для решения многих задачах машинного обучения – по умолчанию использует hinge-loss для задач классификации, то есть по сути в этом сценарии применения является линейным SVM. Кусочно-линейная функция потерь хороша тем, что у нее очень простая производная – положительная константа либо ноль. Это удобно использовать с SGD и большими выборками, когда приходится делать миллиарды обновлений весов.
Про прелести Vowpal Wabbit и обучение на гигабайтах данных за считанные минуты можно почитать в статье открытого курса машинного обучения.
Решение задачи метода опорных векторов#
Итак, метод опорных векторов сводится к решению задачи оптимизации
Для решения таких условных задач оптимизации с условиями в виде неравенств или равенств часто используют лагранжиан и двойственную задачу оптимизации. Этот подход исчерпывающе описан в классической книге Бойда по оптимизации [BV04], а на русском языке можно обратиться к конспекту Евгения Соколова. Также для понимания материала рекомендуется рассмотреть “игрушечный” пример решения задачи метода опорных векторов в случае линейно-разделимой выборки из 5 примеров.
Построим двойственную задачу к задаче метода опорных векторов. Запишем лагранжиан:
Выпишем условия Куна-Таккера:
Проанализируем полученные условия. Из (12) следует, что вектор весов, полученный в результате настройки SVM, можно записать как линейную комбинацию объектов, причем веса в этой линейной комбинации можно найти как решение двойственной задачи.
В зависимости от значений
Отметим, что варианта
Итак, итоговый классификатор зависит только от объектов, лежащих на границе разделяющей полосы, и от объектов-нарушителей (с
Построим двойственную функцию. Для этого подставим выражение (12) в лагранжиан и воспользуемся уравнениями (13) и (14) (данные
три уравнения выполнены для точки минимума лагранжиана при
любых фиксированных
Мы должны потребовать выполнения условий (13) и (14) (если они не выполнены, то двойственная функция обращается в минус бесконечность), а также неотрицательность двойственных переменных
Она также является вогнутой, квадратичной и имеет единственный максимум.
Ядерный переход#
Двойственная задача SVM (18) зависит только от скалярных произведений объектов – отдельные признаковые описания никак не входят в неё.
Note
Обратите внимание, как много это значит: решение SVM зависит только от скалярных произведений объектов (то есть похожести, если упрощать), но не от их признаковых описаний объектов. Это значит, что метод обобщается и на те случаи, когда признаковых описаний объектов нет или их получить очень дорого, но зато есть способ задать расстояние (то есть “измерить сходство”) между объектами.
Значит, можно сделать ядерный переход:
Здесь
Вернемся к тому, какое представление классификатора дает двойственная задача. Из уравнения (12) следует, что вектор весов
Таким образом, классификатор измеряет сходство нового объекта с объектами из обучающей выборки, вычисляя скалярное произведение между ними. Это выражение также зависит только от скалярных произведений, поэтому в нём тоже можно перейти к ядру.
Note
Опять подчеркнем, что классификация нового примера зависит только от скалярных произведений – “похожести” нового примера на примеры из обучающей выборки, и то не все, а только опорные.
Note
В указанном выше представлении фигурирует переменная сдвига
Как правило, для численной устойчивости берут медиану данной величины по всем граничным опорным объектам:
Fig. 76 – пожалуй, самый известный рисунок в контексте SVM, он иллюстрирует ядерный трюк, в свою очередь, одну из самых красивых идей в истории машинного обучения. За счет ядерного перехода можно достигнуть линейной разделимости выборки даже в том случае, когда исходная обучающая выборка не является линейно разделимой.
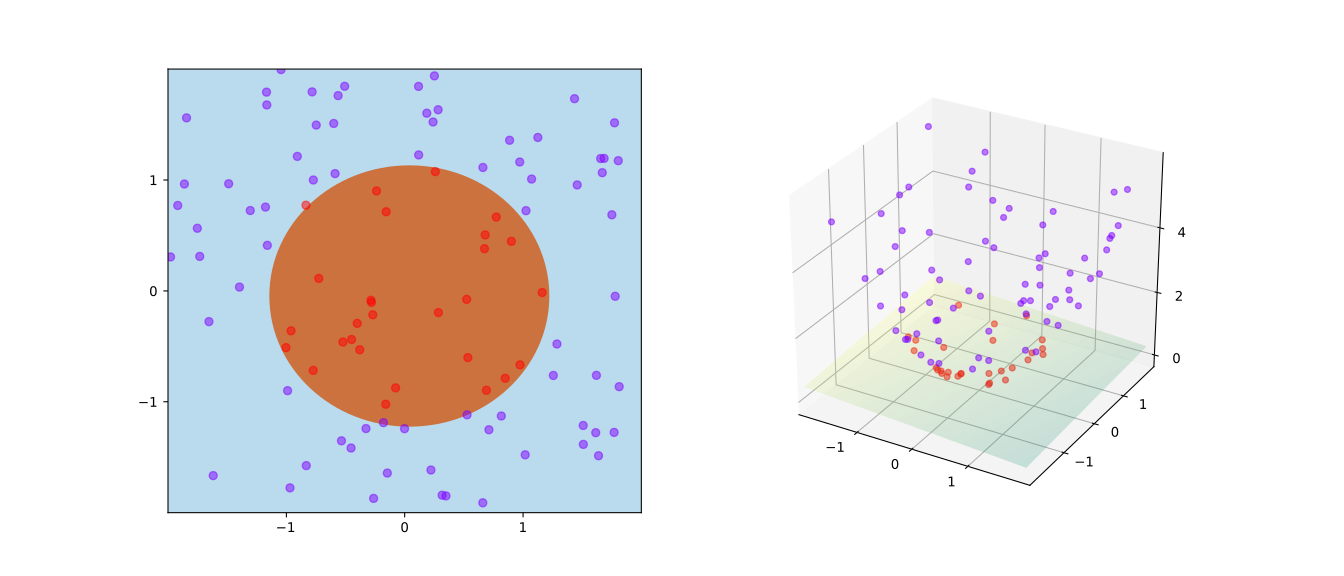
Fig. 76 Пример разделимости в новом пространстве#
Наиболее часто используемые ядра:
Линейное
Полиномиальное ядро
Гауссово ядро, также известное как RBF (radial-basis functions)
Плюсы и минусы SVM#
Плюсы:
хорошо изучены, есть важные теоретические результаты;
красиво формулируется как задача оптимизации;
линейный SVM быстрый, может работать на очень больших выборках;
линейный SVM так же хорошо интерпретируется, как и прочие линейные модели;
решение зависит только от скалярных произведений векторов, а идея “ядерного трюка” – одно из самых красивых в истории машинного обучения;
нелинейный SVM обобщается на работу с самыми разными типами данных (последовательности, графы и т.д.) за счет специфичных ядер.
Минусы:
нелинейный SVM имеет высокую вычислительную сложность и принципиально плохо масштабируется (оптимизационную задачу нельзя “решить на подвыборках” и как-то объединить решения);
нелинейный SVM по сути не интерпретируется (“black box”);
в задачах классификации часто хочется выдать вероятность отнесения к классу, SVM это не умеет делать, а эвристики, как правило, приводят к плохо откалиброванным вероятностям;
ядерный SVM уступает специфичным нейронным сетям уже во многих задачах, например, в в приложениях к графам
