Проблема собственных значений

Автор(ы):

• Синченко Семен

Введение

Мы с вами узнали, что задачи комбинаторной оптимизации и квантовой химии могут быть сведены к решению проблемы поиска минимального собственного значения большого эрмитова оператора – гамильтониана. Для оптимизационных задач это осуществляется при помощи сведения к QUBO-матрице и гамильтониану типа Изинга. А для электронных орбиталей из квантовой химии можно применить преобразование Жордана-Вигнера и также перейти к спиновому гамильтониану.

Теперь перед нами встает вопрос, а как же искать основное состояние этого гамильтониана? В этой лекции рассмотрим классические методы решения этой проблемы, то есть без квантовых компьютеров. Рассмотрение этих методов и их недостатков покажет то, зачем тут так нужен будет квантовый компьютер.

О проблеме (повторение)

Эта тема обсуждалась во вводных лекциях по линейной алгебре, в части про собственные вектора и собственные значения.

Итак, пусть у имеется диагонализируемая матрица $A$ размерности $n\times n$, она же является линейным оператором $\hat{A}$. Из линейной алгебры знаем, что у этой матрицы есть $n$ таких чисел $e_i$ и векторов ${\mathrm{\Psi }}_i$, что для них выполняется условие:

$$A{\mathrm{\Psi }}_i=e_i{\mathrm{\Psi }}_i$$

или в нотации Дирака, которая используется в области квантовых вычислений:

$$\hat{A}|{\mathrm{\Psi }}_i⟩=e_i|{\mathrm{\Psi }}_i⟩$$

Таким образом, собственные вектора – это такие вектора, которые при применении оператора не меняют свое направление. Например, в примере ниже собственный вектор – это ось симметрии оператора:

Fig. 98 Синий вектор, в отличии от красного, при применении оператора не меняет направление так как является его собственным вектором.

Итеративные алгоритмы

В целом, задача нахождения собственных значений является очень трудной с вычислительной точки зрения, особенно для больших матриц. Для матриц размера более, чем $3\times 3$ в общем случае не существует алгоритма нахождения собственных значений и собственных векторов. Однако существует несколько итеративных алгоритмов. Рассмотрим лишь два из них, причем без особых деталей, так как эти алгоритмы, а также доказательство их сходимости являются достаточно сложными.

Степенной метод

Один из самых простых для понимания алгоритмов, который, тем не менее находит интересные применения. Суть его в том, что берем некоторый случайный вектор $|\mathrm{\Psi }⟩$ и начинаем последовательно действовать на него оператором $\hat{A}$ (другими словами умножать, на нашу матрицу), при этом нормируя:

$$|{\mathrm{\Psi }}_{i+1}⟩=\frac{\hat{A}|{\mathrm{\Psi }}_i⟩}{||\hat{A}||}$$

И так повторяем до тех пор, пока изменение вектора не будет меньше, чем некоторое заданное маленькое значение $ϵ$. Когда достигли этого условия, это значит что нашли первый собственный вектор, который соответствует наибольшему собственному значению. В частном случае интересных нам эрмитовых операторов, можно так же последовательно находить все собственные вектора и собственные значения.

Note

На самом деле, сеть интернета является графом – множеством связанных между собой вершин. А любой граф можно представить в виде большой-большой, но очень разреженной матрицы, каждый элемент которой это 1 если между соответствующими вершинами есть ребро и 0, если нет. Например, элемент $L_{ij}$ будет 1, если между вершинами $i$ и $j$ есть ребро.иВ 1998-м году, Ларри Пейдж и Сергей Брин нашли очень эффективный способ подсчета первого собственного вектора этой матрицы, используя именно модификацию степенного метода. Этот алгоритм получил название PageRank, причем Page это фамилия автора, а не отсылка к веб-страницам, как можно было бы подумать. Этот алгоритм лег в основу поисковика Google, который в дальнейшем вырос в транснациональную корпорацию!

Итерация Арнольди

Это гораздо более сложный метод, который, однако, является одним из самых эффективных применительно к разреженным матрицам [Arn51]. Объяснить его легко, к сожалению, не получится, так как алгоритм требует понимания Крыловских подпространств и других концептов из области линейной алгебры разреженных систем. Но пока достаточно лишь того, что этот алгоритм имеет очень эффективную реализацию – ARPACK, написанную в середине 90-х годов на языке FORTRAN77. Именно эта библиотека используется “под капотом” у SciPy, а также во многих других научных пакетах. Давайте посмотрим, как она работает.

Сгенерируем большую разреженную матрицу.

import numpy as np
from scipy import sparse

np.random.seed(42)
x = np.random.random(10000)
np.random.seed(42)
y = np.random.random(10000)
px = np.where(x > 0.2)
py = np.where(y > 0.2)
num_elements = max([px[0].shape[0], py[0].shape[0]])
spmat = sparse.coo_matrix(
    (
        (np.ones(num_elements),
        (px[0][:num_elements], py[0][:num_elements]))
    )
)

print(spmat.__repr__())

<10000x10000 sparse matrix of type '<class 'numpy.float64'>'
	with 7957 stored elements in COOrdinate format>

Матрица размера $10000\times 10000$ это большая матрица и работать с ней в “плотном” (dense) представлении было бы очень трудно. Но ARPACK позволяет найти минимальное собственное значение за доли секунд, используя разреженность матрицы:

from scipy.sparse import linalg as sl

max_eigval = sl.eigs(spmat, k=1, which="LR", return_eigenvectors=False)[0]
min_eigval = sl.eigs(spmat, k=1, which="SR", return_eigenvectors=False)[0]

print(f"Min E: {min_eigval}\nMax E: {max_eigval}")

Min E: (-1.1102230246251565e-16+0j)
Max E: (1.0000000000000007+0j)

Для тех кто забыл, какие параметры принимает функция eigs из scipy.linalg.spare напомним, что первый параметр это разреженная матрица, k – сколько именно собственных значений хотим получить, which указывает на собственные значения:

• SM – smallest magnitude – наименьшие по модулю числа

• LM – largest magnitude – наибольшие по модулю числа

• SR – smallers real – числа с наименьшей действительной частью

• LR – largest real – числа с наибольшей действительной частью

• SI – smallest image – числа с наименьшей мнимой частью

• LI – largest image – числа с наибольшей мнимой частью

Наконец, параметр return_eigenvectors – хотим ли получить только собственные значения, или еще и собственные вектора.

Более подробна работа с scipy.sparse, а также с scipy.sparse.linalg разбирается в [вводном блоке по линейной алгебре](пока пусто).

Note

Не у всех матриц все собственные значения являются действительными, поэтому ARPACK по умолчанию считает комплексные значения, хотя в этом конкретном случае видим, что мнимая часть равна нулю.

Алгоритм Ланкзоша

Итерация Ланкзоша (англ. Lanzos) [Lan50] – это модификация итерации Арнольди, которая работает с эрмитовыми матрицами и находит максимально широкое применение в том числе для квантовых гамильтонианов. Этот алгоритм по умолчанию включен в большинство математических пакетов, включая ARPACK и, соответственно, SciPy:

max_eigval = sl.eigsh(spmat, k=1, which="LM", return_eigenvectors=False)[0]
min_eigval = sl.eigsh(spmat, k=1, which="SM", return_eigenvectors=False)[0]

print(f"Min E: {min_eigval}\nMax E: {max_eigval}")

Min E: -8.323011768995762e-25
Max E: 1.0000000000000002

У этой процедуры из ARPACK немного другие варианты параметра which, так как мы помним, что у эрмитовых матриц собственные значения вещественны:

• LM – largest magnitude – наибольшие по модулю

• SM – smallest magnitude – наименьшие по модулю

• LA – largest algebraic – алгебраически наибольшие, т.е. с учетом знака

• SA – smallest algebraic – алгебраически наименьшие, т.е. с учетом знака

Вариационные алгоритмы

В этом разделе поговорим о существующих алгоритмах решения задачи об основном состоянии уже в контексте квантовой механики. Хотя, как помним, задачи оптимизации и квантовой физики тесно связаны. В каком-то смысле, вариационные алгоритмы, а в особенности, квантовый Монте-Карло и различные его модификации в чем-то сильно похожи на классический алгоритм имитации отжига.

Вариационный Монте-Карло

Variational Monte-Carlo, или просто VMC это очень простой и в тоже время эффективный алгоритм нахождения основного состояния квантомеханической системы.

Note

Замечание – в классическом VMC обычно работают при нулевой температуре. Хотя в общем случае, температура оказывает значительное влияние на то, в каком состоянии находится физическая система.

Давайте еще раз запишем ожидаемое значение энергии гамильтониана в состоянии $|\mathrm{\Psi }⟩$:

$$E=\frac{⟨\mathrm{\Psi }|\hat{H}|\mathrm{\Psi }⟩}{⟨\mathrm{\Psi }|\mathrm{\Psi }⟩}$$

Если ввести вектор $X$, который описывает конфигурацию системы (например, ориентации спинов), то выражение для энергии можно переписать в интегральной форме:

$$E=\frac{\int |\mathrm{\Psi }(X){|}^2\frac{\hat{H}\mathrm{\Psi }(X)}{\mathrm{\Psi }(X)}dX}{\int |\mathrm{\Psi }(X){|}^{2}dX}$$

В данном случае, выражение

$$\frac{|\mathrm{\Psi }(X){|}^2}{\int |\mathrm{\Psi }(X){|}^{2}dX}$$

дает распределение вероятностей, а значит можно из него семплировать, используя методы Монте-Карло. Это очень похоже на то, как ранее семплировали из распределения Больцмана в классическом методе Монте-Карло. Вопрос лишь в том, как представить волновую функцию $|\mathrm{\Psi }⟩$? В этом помогут так называемые trial wave functions – параметризированные функции от $X$. В этом случае меняем или варьируем параметры trial wave function в процессе:

• семплируем из $\frac{|\mathrm{\Psi }(X){|}^2}{\int |\mathrm{\Psi }(X){|}^{2}dX}$ конфигурации;

• обновляем параметризацию trial function так, чтобы минимизировать энергию.

Повторяем до сходимости. Ну а дальше посмотрим на некоторые примеры trial wave functions.

Jastrow Function

Когда есть задача из $N$ квантовых частиц, каждая из которых описывается координатой или радиус вектором, то можно построить trial wave function в виде суммы попарных функций двухчастичных взаимодействий:

$$\mathrm{\Psi }(X)=e^{-\sum _{i,j}u(r_i,r_j)},$$

где $r_i,r_j$ – это радиус-векторы частиц, а $u(r_i,r_j)$ – симметричная функция, описывающая двухчастичное взаимодействия. Такая функция называется Jastrow function [Jas55]. В этом случае, в процессе работы VMC будем просто варьировать радиус-векторы частиц также, как варьировали вершины графа в обычном отжиге, когда решали задачу комбинаторной оптимизации. Только теперь есть еще и параметризация обменных взаимодействий, которую “варьируем”.

Hartree-Fock (SCF)

Для задач квантовой химии, когда работаем с фермионами, существует вид trial wave function на основе Слэтеровского детерминанта, о котором писали в продвинутой лекции по квантовой химии:

$$\mathrm{\Psi }(R)=D^{\uparrow }{D}^{\downarrow },$$

где $D$ это матрица из одноэлектронных орбиталей:

$$\begin{array}{r}D=\left[\begin{array}{cccc}{\psi }_1(r_1)& {\psi }_1(r_2)& ...& {\psi }_1(r_{N/2})\\ ...& ...& ...& ...\\ {\psi }_{N/2}(r_1)& {\psi }_{N/2}(r_2)& ...& {\psi }_{N/2}(r_{N/2})\end{array}\right]\end{array}$$

Jastrow Function для спинов

Дальше нас будут интересовать как раз модели Изинга и спины, а не частицы в пространстве или орбитали из вторичного квантования. Для спинов можем записать Jastrow function следующим образом:

$$\mathrm{\Psi }(s)=e^{\sum _{i,j}{s}_i{W}_{i,j}{s}_j},$$

где матрица $W$ будет играть роль параметризации и отражать парные спиновые корреляции. Давайте посмотрим это на практике при помощи библиотеки NetKet [CCH+19].

import netket as nk

Моделировать будем простую модель Изинга для цепочки из 10 спинов (чтобы быстро считалось):

$$\hat{H}=-h\sum _i{\sigma }_i^x+J\sum _{i,j}{\sigma }_i^z{\sigma }_j^z$$

Параметры возьмем такими:

• $J=0.5$

• $h=1.321$

g = nk.graph.Hypercube(length=10, n_dim=1, pbc=True)
hi = nk.hilbert.Spin(s=0.5, N=g.n_nodes)
op = nk.operator.Ising(h=1.321, hilbert=hi, J=0.5, graph=g)

Поскольку модель относительно небольшая по числу частиц, то сразу можем получить точное решение методом Ланкзоша.

exact = nk.exact.lanczos_ed(op)[0]

Создадим модель на основе Jastrow и VMC:

sampler = nk.sampler.MetropolisLocal(hi)
model = nk.models.Jastrow(dtype=complex)
optimizer = nk.optimizer.Sgd(learning_rate=0.05)
sr = nk.optimizer.SR(diag_shift=0.01)
vmc = nk.driver.VMC(op, optimizer, sampler, model, n_samples=1008, preconditioner=sr)

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/netket/utils/deprecation.py:126: FutureWarning: 

**DEPRECATION_WARNING:**
    The `dtype` argument to neural-network layers and models is deprecated
    throughout NetKet to maintain consistency with new releases of flax.
    Please use `param_dtype` instead.

    This warning will become an error in a future version of NetKet.


  warn_deprecation(_dep_msg)
WARNING:absl:No GPU/TPU found, falling back to CPU. (Set TF_CPP_MIN_LOG_LEVEL=0 and rerun for more info.)

Note

Изучение документации библиотеки NetKet оставляем вам самим, так как объяснение абстракций графа и гильбертова пространства, а также использование метода stochastic reconfiguration для вычисления градиентов выходит за рамки лекции. Документаци представлена на сайте NetKet.

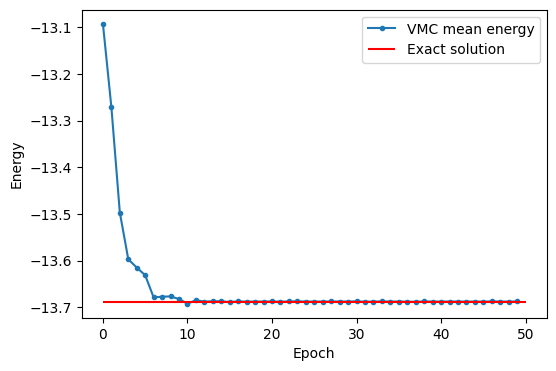
Запустим оптимизацию:

logger = nk.logging.RuntimeLog()
vmc.run(50, out=logger, show_progress=False)

(RuntimeLog():
  keys = ['Energy'],)

Посмотрим на результат:

import matplotlib.pyplot as plt

plt.figure(figsize=(6, 4))
plt.plot(list(range(50)), np.real(logger.data["Energy"]["Mean"]), ".-", label="VMC mean energy")
plt.xlabel("Epoch")
plt.ylabel("Energy")
plt.hlines(exact, 0, 50, label="Exact solution", color="red")
plt.legend()
plt.show()

Neural Network Quantum States

Еще более интересный подход к выбору trial wave function – это использование в качестве $\mathrm{\Psi }(X)$ нейронной сети [CT17]. Уже немного касались этой темы, когда речь шла о видах квантового машинного обучения. Хороший вариант, это использовать, например, полносвязную сеть – ограниченную машину Больцмана:

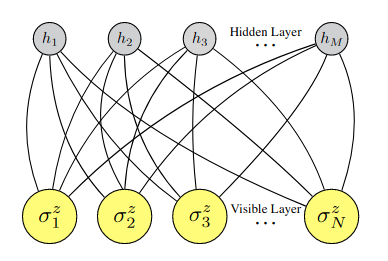
Fig. 99 Нейронная сеть в качестве trial wave function из работы [CT17].

Это также легко может быть реализовано с использованием библиотеки NetKet:

model = nk.models.RBM()
optimizer = nk.optimizer.Sgd(learning_rate=0.05)
sr = nk.optimizer.SR(diag_shift=0.01)
vmc = nk.driver.VMC(op, optimizer, sampler, model, n_samples=1000, preconditioner=sr)

logger = nk.logging.RuntimeLog()
vmc.run(50, out=logger, show_progress=False)

plt.figure(figsize=(6, 4))
plt.plot(list(range(50)), np.real(logger.data["Energy"]["Mean"]), ".-", label="VMC mean energy")
plt.xlabel("Epoch")
plt.ylabel("Energy")
plt.hlines(exact, 0, 50, label="Exact solution", color="red")
plt.legend()
plt.show()

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/netket/vqs/mc/mc_state/state.py:58: UserWarning: n_samples=1000 (1000 per MPI rank) does not divide n_chains=16, increased to 1008 (1008 per MPI rank)
  warnings.warn(

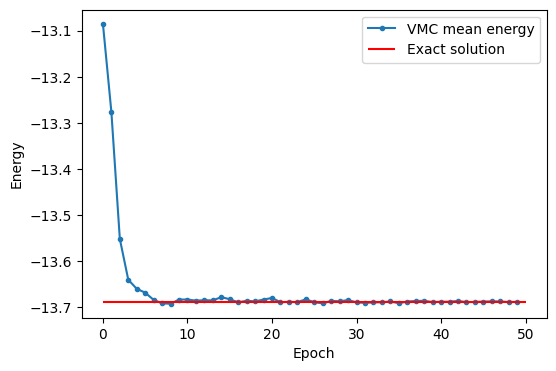
Преимущества использования нейронной сети трудно показать на таком небольшом примере с моделью Изинга и 10-ю спинами, но они полностью раскрываются, если нужно анализировать более сложные модели.

Note

Это интересно, но при помощи библиотеки NetKet можно по сути решать проблемы комбинаторной оптимизации [SB19] с помощью методов deep learning.

Проблемы с VMC

К сожалению, у метода VMC есть свои проблемы. Это относительно плохая масштабируемость – при росте размерности проблемы для того, чтобы подобрать реально хорошую аппроксимацию потребуется все больше итераций и семплов на каждой из них. Также у VMC есть ряд фундаментальных проблем, например, так называемая sign problem [LJGS+90].

Заключение

В этой лекции рассмотрены известные подходы к решению задачи о минимальном собственном значении на классическом компьютере. Как увидели, все эти методы не могут быть масштабированы на реально большие операторы. Так что для решения этих проблем действительно нужен квантовый компьютер.