Классический SVM

Автор(ы):

• Кашницкий Юрий

Описание лекции

В этой лекции мы рассмотрим классический метод опорных векторов (SVM) и разберем стоящую за ним математику. С согласия Евгения Соколова, мы во многом переиспользуем конспекты лекций курса “Машинное обучение”, читаемого на ФКН ВШЭ.

План лекции такой:

• линейная классификация;

• интуиция метода опорных векторов;

• метод опорных векторов для линейно-разделимой выборки;

• метод опорных векторов для линейно-неразделимой выборки;

• решение задачи метода опорных векторов;

• ядерный переход;

• плюсы и минусы SVM.

Линейная классификация

Основная идея линейного классификатора заключается в том, что признаковое пространство может быть разделено гиперплоскостью на два полупространства, в каждом из которых прогнозируется одно из двух значений целевого класса. Если это можно сделать без ошибок, то обучающая выборка называется линейно разделимой.

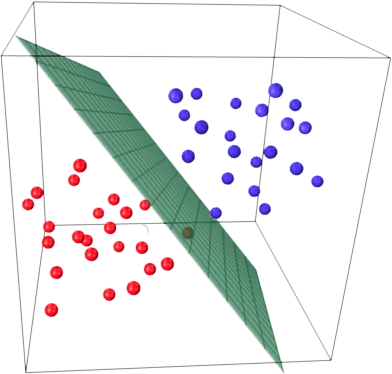
Fig. 71 Линейная классификация

Рассмотрим задачу бинарной классификации, в которой $\mathbb{X}={\mathbb{R}}^d$ – пространство объектов, $Y=\{-1,+1\}$ – множество допустимых ответов (целевой признак), $X=\{(x_i,y_i){\}}_{i=1}^{\ell }$ – обучающая выборка. Будем класс $+1$ называть положительным, а класс $-1$ – отрицательным. Здесь $d$ – размерность признакового пространства, $\ell$ – количество примеров в обучающей выборке.

Линейная модель классификации определяется следующим образом:

$$a(x)=\text{sign}(⟨w,x⟩+b)=\text{sign}(\sum _{j=1}^d{w}_j{x}_j+b),$$

где $w\in {\mathbb{R}}^d$ – вектор весов, $b\in \mathbb{R}$ – сдвиг (bias), $\text{sign}(\cdot )$ – функция “сигнум”, возвращающая знак своего аргумента, $a(x)$ – ответ классификатора на примере $x$.

Note

Хорошо бы для векторов ставить стрелку и писать $\overrightarrow{w}$, но мы этого не будем делать, предполагая, что из контекста ясно, что вектор, а что скаляр. В частности, в формуле выше $w$ и $x$ – вектора, а $a(x),w_j,x_j,d$ и $b$ – скаляры.

Часто считают, что среди признаков есть константа, $x_{d+1}=1$. В этом случае нет необходимости вводить сдвиг $b$, и линейный классификатор можно задавать как

$$a(x)=\text{sign}⟨w,x⟩.$$

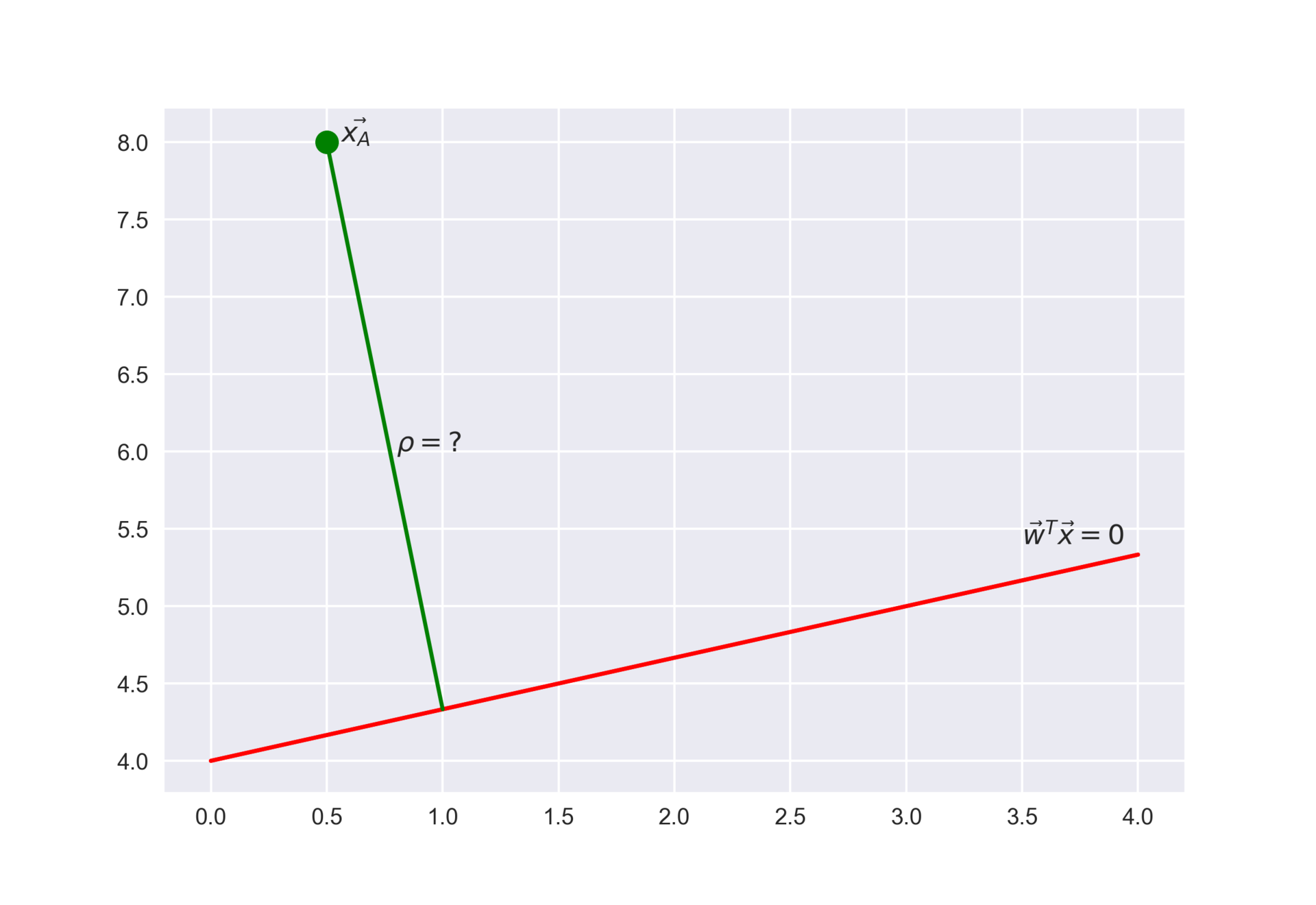
Fig. 72 Расстояние от точки до плоскости

Геометрически линейный классификатор соответствует гиперплоскости с вектором нормали $w$, которая задается уравнением $⟨w,x⟩=0$. Величина скалярного произведения $⟨w,x⟩$ пропорциональна расстоянию от гиперплоскости до точки $x$, а его знак показывает, с какой стороны от гиперплоскости находится данная точка. Если быть точным, расстояние от точки с радиус-вектором $x_A$ до плоскости $⟨w,x⟩=0$:

$$\rho (x_A,⟨w,x⟩=0)=\frac{⟨w,x_A⟩}{||w||}.$$

Упражнение на метод Лагранжа

Метод Лагранжа – очень важный метод оптимизации функций при наличии органичений. Этот же метод вовсю используется ниже в методе опорных векторов.

Рекомендуется ознакомиться с методом Лагранжа и решить (ручками!) простую оптимизационную задачу вида

$$\begin{array}{r}\{\begin{array}{rl}& x+y\to \underset{x,y}{min}\\ & x^2+y^2=1\end{array}\end{array}$$

А мы выведем указанную выше формулу расстояния от точки до плоскости. Вообще это можно сделать разными способами – алгебраически и геометрически. Но давайте посмотрим на эту задачу (внезапно) как на задачу оптимизации и решим ее методом Лагранжа. Это послужит неплохой тренировкой перед тем как окунуться в SVM.

Итак, представим задачу в таком виде: хотим найти точку $x$ на плоскости $⟨w,x⟩=0$ такую, что расстояние от $x$ до точки $x_0$ минимально:

$$\begin{array}{r}\{\begin{array}{rl}& \rho (x,x_0)\to \underset{x}{min}\\ & ⟨w,x⟩=0\end{array}\end{array}$$

Лагранжиан: $\mathcal{L}(x,\lambda )={||x-x_0||}^2+2\lambda ⟨w,x⟩$. Тут мы для $\rho (x,x_0)$ подставили квадрат расстояния ${||x-x_0||}^2$ (такой переход от росстояния к его квадрат хорошо бы обосновать монотонностью оптимизируемой функции, но мы это опустим), а также перед коэффициентом $\lambda$ для удобства поставили 2, что несущественно.

Далее надо приравнять нулю частные производные лагранжиана по его аргументам. Из $\frac{\partial \mathcal{L}}{\partial x}=0$ получаем: $2(x-x_0)+2\lambda w=0\Rightarrow x=x_0-\lambda w$.

Теперь домножим это уравнение скалярно на $w$ и выразим $\lambda$:

$$⟨w,x⟩=⟨w,x_0⟩-\lambda {||w||}^2\Rightarrow \lambda =\frac{⟨w,x_0⟩}{{||w||}^2}$$

Тогда наконец

$$\underset{x,⟨w,x⟩=0}{min}\rho (x,x_0)=||x-x_0||=||(x_0-\lambda w)-x_0||=|\lambda |||w||=\frac{⟨w,x_0⟩}{||w||}◻.$$

Таким образом, линейный классификатор разделяет пространство на две части с помощью гиперплоскости, и при этом одно полупространство относит к положительному классу, а другое – к отрицательному.

Пожалуй, самый известный и популярный на практике представитель семейства линейных классификаторов – логистическая регрессия. На русском языке про нее можно почитать в статье открытого курса по машинному обучению или в упомянутых лекциях Евгения Соколова. В этих лекциях также объясняется, как происходит обучение модели (подбор весов $w$) за счет минимизации функции потерь.

Отступ классификации

Оказывается полезным рассмотреть выражение $M(x_i,y_i,w)=y_i\cdot ⟨w,x⟩.$

Это отступ классификации (margin) для объекта обучающей выборки $(x_i,y_i)$. К сожалению, его очень легко перепутать с зазором классификации, который появится чуть ниже в изложении интуиции метода опорных векторов. Чтобы не путать: отступ определен на конкретном объекте обучающей выборки.

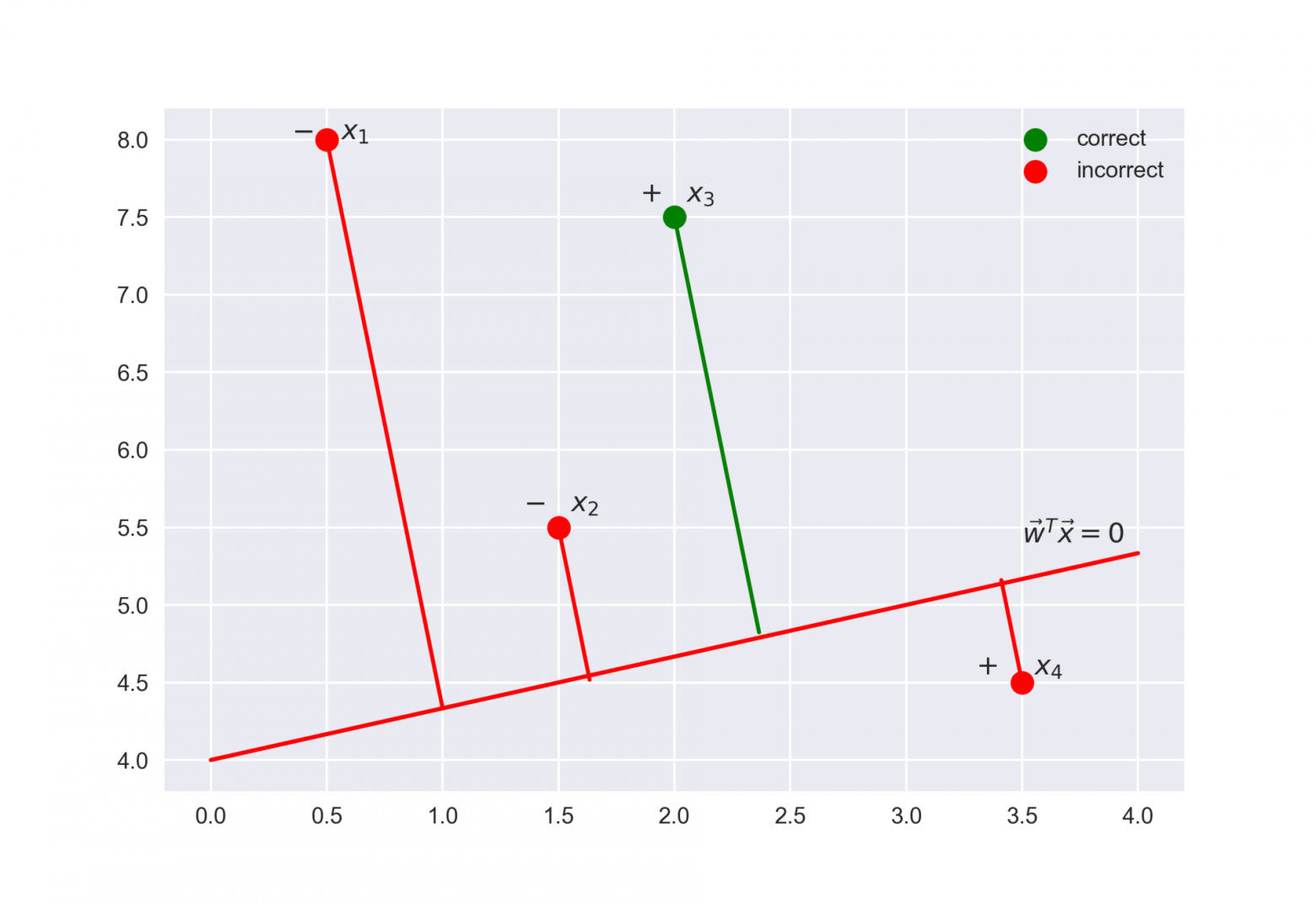
Fig. 73 Иллюстрация к понятию отступа классификации

Отступ – это своего рода “уверенность” модели в классификации объекта $(x_i,y_i)$:

• если отступ большой (по модулю) и положительный, это значит, что метка класса поставлена правильно, а объект находится далеко от разделяющей гиперплоскости (такой объект классифицируется уверенно). На рисунке – $x_3$.

• если отступ большой (по модулю) и отрицательный, значит метка класса поставлена неправильно, а объект находится далеко от разделяющей гиперплоскости (скорее всего такой объект – аномалия, например, его метка в обучающей выборке поставлена неправильно). На рисунке – $x_1$.

• если отступ малый (по модулю), то объект находится близко к разделяющей гиперплоскости, а знак отступа определяет, правильно ли объект классифицирован. На рисунке – $x_2$ и $x_4$.

Далее увидим, что понятие отступа классификации – часть функции потерь, которая оптимизируется в методе опорных векторов.

Интуиция метода опорных векторов

Метод опорных векторов (Support Vector Machine, SVM) основан на идее максимизации зазора между классами. Пока не вводим этот термин формально, но передадим интуицию метода. На Рис. Fig. 74 показана линейно-разделимая выборка, кружки соответствуют положительным примерам, а квадраты – отрицательным (или наоборот), а оси – некоторым признакам этих примеров. На рисунке слева показаны две прямые (в общем случае – гиперплоскости), разделяющие выборку. Кажется, что синяя прямая лучше тем, что она дальше отстоит от примеров обучающей выборки, чем красная прямая (зазор – больше), и потому лучше будет разделять другие примеры из того же распределения, что и примеры обучающей выборки. То есть такой линейный классификатор будет лучше обобщаться на новые данные. Теория подтверждает описанную интуицию [MRT18].

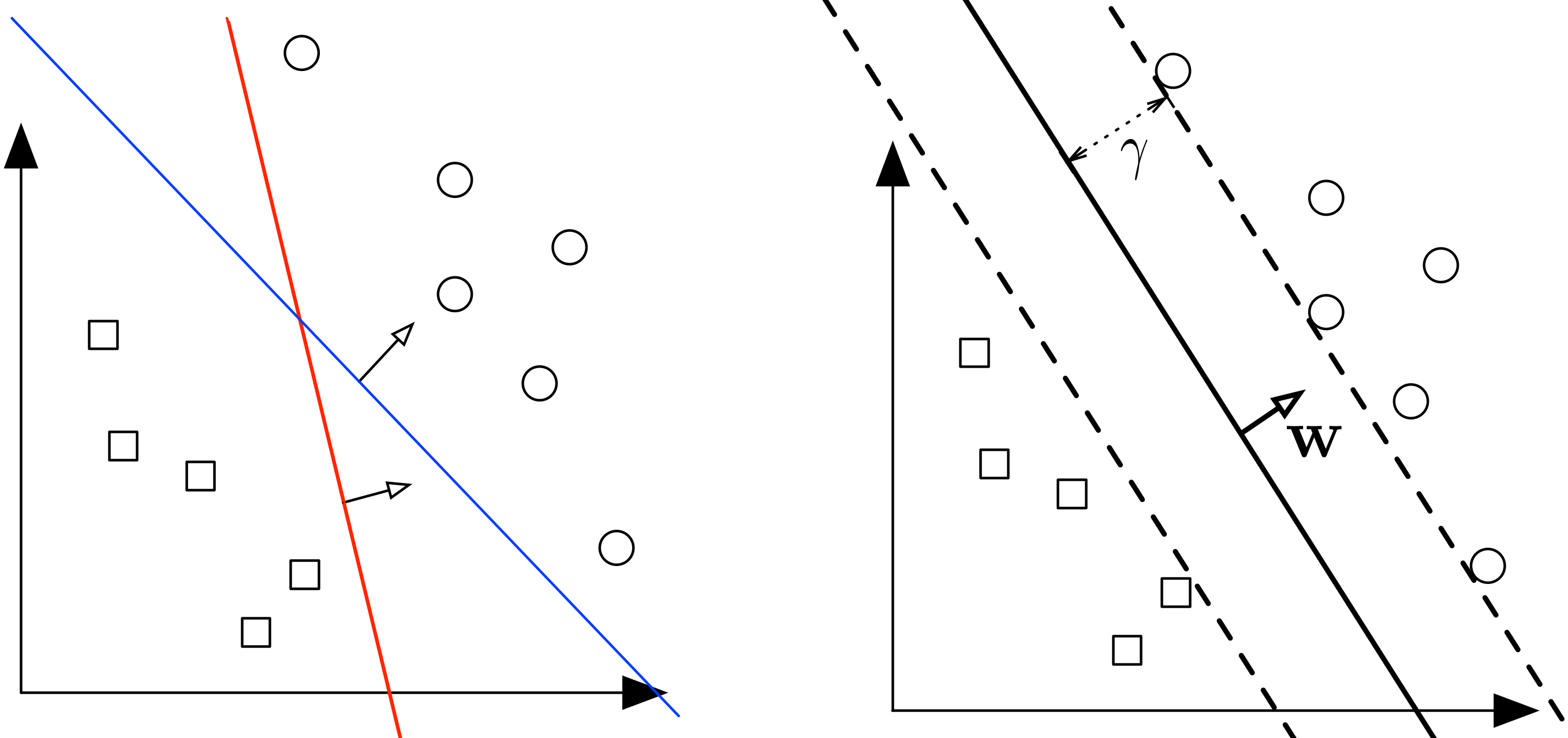
Fig. 74 Слева показаны две прямые (в общем случае – гиперплоскости), разделяющие выборку. Справа показана прямая, максимизирующая зазор между классами. Источник: лекция Cornell

Note

Одним из ключевых авторов алгоритма SVM является Владимир Вапник – советский и американский (с 1991-го года) ученый, который также сделал огромный вклад в теорию классического машинного обучения. Его имя носит одно из ключевых теоретических понятий машинного обучения – размерность Вапника-Червоненкиса.

Метод опорных векторов для линейно-разделимой выборки

Будем рассматривать линейные классификаторы вида

$$a(x)=\text{sign}(⟨w,x⟩+b),w\in {\mathbb{R}}^d,b\in \mathbb{R}.$$

Заметьте, что мы вернули сдвиг (bias) $b$. Будем считать, что существуют такие параметры $w_{\ast }$ и $b_{\ast }$, что соответствующий им классификатор $a(x)$ не допускает ни одной ошибки на обучающей выборке. В этом случае говорят, что выборка линейно разделима.

Заметим, что если одновременно умножить параметры $w$ и $b$ на одну и ту же положительную константу, то классификатор не изменится. Распорядимся этой свободой выбора и отнормируем параметры так, что

$$\underset{x\in X}{min}|⟨w,x⟩+b|=1.$$

Как мы увидели выше, расстояние от произвольной точки $x_0\in {\mathbb{R}}^d$ до гиперплоскости, определяемой данным классификатором, равно

$$\rho (x_0,a)=\frac{|⟨w,x⟩+b|}{\parallel w\parallel }.$$

Тогда расстояние от гиперплоскости до ближайшего примера из обучающей выборки равно

$$\underset{x\in X}{min}\frac{|⟨w,x⟩+b|}{\parallel w\parallel }=\frac{1}{\parallel w\parallel }\underset{x\in X}{min}|⟨w,x⟩+b|=\frac{1}{\parallel w\parallel }.$$

Данная величина также называется зазором (margin). Опять же, эту величину очень легко перепутать с отступом классификации, про который мы говорили выше и который тоже margin в англоязычном варианте. Заметим, что отступ – функция параметров $w$ и конкретного примера обучающей выборки $(x_i,y_i)$, а зазор – функция только параметров $w$ при описанном трюке с нормировкой $w$ и $b$ (в противном случае зазор – также функция сдвига $b$ и всех примеров $x$).

Таким образом, если классификатор без ошибок разделяет обучающую выборку, то ширина его разделяющей полосы равна $\frac{2}{\parallel w\parallel }$. Максимизация ширины разделяющей полосы приводит к повышению обобщающей способности классификатора [MRT18]. На повышение обобщающей способности направлена и регуляризация, которая штрафует большую норму весов – а чем больше норма весов, тем меньше ширина разделяющей полосы.

Итак, требуется построить классификатор, идеально разделяющий обучающую выборку, и при этом имеющий максимальный отступ.

Запишем соответствующую оптимизационную задачу, которая и будет определять метод опорных векторов для линейно разделимой выборки (hard margin support vector machine):

$$\begin{array}{r}\{\begin{array}{rl}& \frac{1}{2}\parallel w{\parallel }^2\to \underset{w,b}{min}\\ & y_i(⟨w,x_i⟩+b)\ge 1,i=1,\dots ,\ell .\end{array}\end{array}$$

Здесь мы воспользовались тем, что линейный классификатор дает правильный ответ на примере $x_i$ тогда и только тогда, когда $y_i(⟨w,x_i⟩+b)\ge 0$ (вспомним, что $M_i=y_i(⟨w,x_i⟩+b)$ – отступ классификации для примера $(x_i,y_i)$ обучающей выборки). Более того, из условия нормировки $\underset{x\in X}{min}|⟨w,x⟩+b|=1$ следует, что $y_i(⟨w,x_i⟩+b)\ge 1$.

В данной задаче функционал является строго выпуклым, а ограничения линейными, поэтому сама задача является выпуклой и имеет единственное решение. Более того, задача является квадратичной и может быть решена крайне эффективно.

Метод опорных векторов для линейно-неразделимой выборки

Рассмотрим теперь общий случай, когда выборку невозможно идеально разделить гиперплоскостью. Это означает, что какие бы $w$ и $b$ мы ни взяли, хотя бы одно из ограничений в предыдущей задаче будет нарушено:

$$\mathrm{\exists }{x}_i\in X:y_i(⟨w,x_i⟩+b)<1.$$

Сделаем эти ограничения мягкими, введя штраф ${\xi }_i\ge 0$ за их нарушение:

$$y_i(⟨w,x_i⟩+b)\ge 1-{\xi }_i,i=1,\dots ,\ell .$$

Отметим, что если отступ объекта лежит между нулем и единицей ($0\le y_i(⟨w,x_i⟩+b)<1$), то объект верно классифицируется, но имеет ненулевой штраф $\xi >0$. Таким образом, мы штрафуем объекты за попадание внутрь разделяющей полосы.

Величина $\frac{1}{\parallel w\parallel }$ в данном случае называется мягким зазором (soft margin). С одной стороны, мы хотим максимизировать зазор, с другой – минимизировать штраф за неидеальное разделение выборки $\sum _{i=1}^{\ell }{\xi }_i$.

Эти две задачи противоречат друг другу: как правило, излишняя подгонка под выборку приводит к маленькому зазору, и наоборот – максимизация зазора приводит к большой ошибке на обучении. В качестве компромисса будем минимизировать взвешенную сумму двух указанных величин.

Приходим к оптимизационной задаче, соответствующей методу опорных векторов для линейно неразделимой выборки (soft margin support vector machine):

$$\begin{array}{r}\{\begin{array}{rl}& \frac{1}{2}\parallel w{\parallel }^2+C\sum _{i=1}^{\ell }{\xi }_i\to \underset{w,b,\xi }{min}\\ & y_i(⟨w,x_i⟩+b)\ge 1-{\xi }_i,i=1,\dots ,\ell ,\\ & {\xi }_i\ge 0,i=1,\dots ,\ell .\end{array}\end{array}$$

Чем больше здесь параметр $C$, тем сильнее мы будем настраиваться на обучающую выборку. Данная задача также является выпуклой и имеет единственное решение.

Сведение к безусловной задаче оптимизации

Покажем, что задачу метода опорных векторов можно свести к задаче безусловной оптимизации функционала, который имеет вид верхней оценки на долю неправильных ответов.

Перепишем условия задачи:

$$\begin{array}{r}\{\begin{array}{rl}& {\xi }_i\ge 1-y_i(⟨w,x_i⟩+b)\\ & {\xi }_i\ge 0\end{array}\end{array}$$

Поскольку при этом в функционале требуется, чтобы штрафы ${\xi }_i$ были как можно меньше, то можно получить следующую явную формулу для них:

$${\xi }_i=max(0,1-y_i(⟨w,x_i⟩+b)).$$

Данное выражение для ${\xi }_i$ уже учитывает в себе все ограничения задачи, описанной выше. Значит, если подставить его в функционал, получим безусловную задачу оптимизации:

$$\frac{1}{2}\parallel w{\parallel }^2+C\sum _{i=1}^{\ell }max(0,1-y_i(⟨w,x_i⟩+b))\to \underset{w,b}{min}$$

Эта задача является негладкой, поэтому решать её может быть достаточно тяжело. Тем не менее, она показывает, что метод опорных векторов, по сути, как и логистическая регрессия, строит верхнюю оценку на долю ошибок и добавляет к ней стандартную квадратичную регуляризацию. Только если в случае логистической регрессии этой верхней оценкой была логистическая функция потерь (опять сделаем отсылку к статье из открытого курса машинного обучения), то в случае метода опорных векторов это функция вида $L(y,z)=max(0,1-yz)$, которая называется кусочно-линейной функцией потерь (hinge loss).

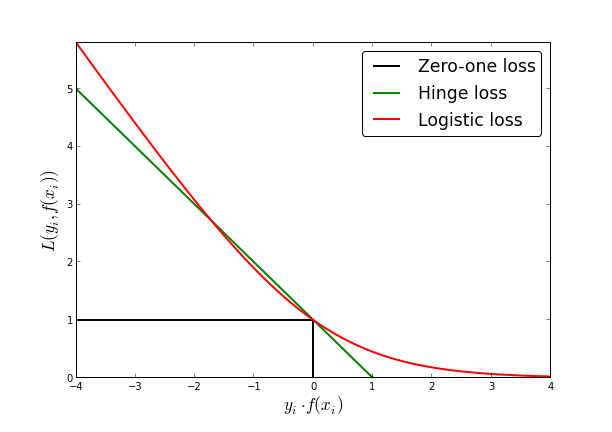
Fig. 75 Пороговая, кусочно-линейная и логистическая функции потерь

Это становится понятнее в терминах упомянутого выше отступа $M_i=y_i(⟨w,x_i⟩+b)$ на примере обучающей выборки. В идеале мы хотели бы штрафовать классификатор за ошибку на примере: $L_{1/0}(M_i)=[M_i<0]$. Это пороговая функция потерь (zero-one loss), ее график изображен черным на Fig. 75 как функция от отступа. К сожалению, напрямую мы не можем эффективно оптимизировать такую функцию градиентными методами из-за разрыва в нуле, поэтому оптимизируется верхняя оценка zero-one loss. В случае логистической регрессии – логистическая функция потерь $L(M_i)=\log (1+e^{-M_i})$ (красная на рисунке выше), а в случае метода опорных векторов – кусочно-линейная функция $L(M_i)=max(0,1-M_i)$ (зеленая на рисунке выше).

Note

Бытует мнение, что метод опорных векторов сегодня нигде не используется из-за его сложности (как минимум квадратичной по числу примеров). Однако, это не так. Линейный SVM вполне неплохо можно применять в задачах с высокой размерностью объектов обучающей выборки, например, для классификации текстов с Tf-Idf или любым другим разреженным представлением. В частности, Vowpal Wabbit – очень эффективная утилита для решения многих задачах машинного обучения – по умолчанию использует hinge-loss для задач классификации, то есть по сути в этом сценарии применения является линейным SVM. Кусочно-линейная функция потерь хороша тем, что у нее очень простая производная – положительная константа либо ноль. Это удобно использовать с SGD и большими выборками, когда приходится делать миллиарды обновлений весов.

Про прелести Vowpal Wabbit и обучение на гигабайтах данных за считанные минуты можно почитать в статье открытого курса машинного обучения.

Решение задачи метода опорных векторов

Итак, метод опорных векторов сводится к решению задачи оптимизации

$$\begin{array}{r}\{\begin{array}{rl}& \frac{1}{2}\parallel w{\parallel }^2+C\sum _{i=1}^{\ell }{\xi }_i\to \underset{w,b,\xi }{min}\\ & y_i(⟨w,x_i⟩+b)\ge 1-{\xi }_i,i=1,\dots ,\ell ,\\ & {\xi }_i\ge 0,i=1,\dots ,\ell .\end{array}\end{array}$$

Для решения таких условных задач оптимизации с условиями в виде неравенств или равенств часто используют лагранжиан и двойственную задачу оптимизации. Этот подход исчерпывающе описан в классической книге Бойда по оптимизации [BV04], а на русском языке можно обратиться к конспекту Евгения Соколова. Также для понимания материала рекомендуется рассмотреть “игрушечный” пример решения задачи метода опорных векторов в случае линейно-разделимой выборки из 5 примеров.

Построим двойственную задачу к задаче метода опорных векторов. Запишем лагранжиан:

$$L(w,b,\xi ,\lambda ,\mu )=\frac{1}{2}\parallel w{\parallel }^2+C\sum _{i=1}^{\ell }{\xi }_i-\sum _{i=1}^{\ell }{\lambda }_i[y_i(⟨w,x_i⟩+b)-1+{\xi }_i]-\sum _{i=1}^{\ell }{\mu }_i{\xi }_i.$$

Выпишем условия Куна-Таккера:

(12)$${\mathrm{\nabla }}_{w}L=w-\sum _{i=1}^{\ell }{\lambda }_i{y}_i{x}_i=0⟹w=\sum _{i=1}^{\ell }{\lambda }_i{y}_i{x}_i$$

(13)$${\mathrm{\nabla }}_{b}L=-\sum _{i=1}^{\ell }{\lambda }_i{y}_i=0⟹\sum _{i=1}^{\ell }{\lambda }_i{y}_i=0$$

(14)$${\mathrm{\nabla }}_{{\xi }_i}L=C-{\lambda }_i-{\mu }_i⟹{\lambda }_i+{\mu }_i=C$$

(15)$${\lambda }_i[y_i(⟨w,x_i⟩+b)-1+{\xi }_i]=0⟹({\lambda }_i=0)\text{или}(y_i(⟨w,x_i⟩+b)=1-{\xi }_i)$$

(16)$${\mu }_i{\xi }_i=0⟹({\mu }_i=0)\text{или}({\xi }_i=0)$$

(17)$${\xi }_i\ge 0,{\lambda }_i\ge 0,{\mu }_i\ge 0.$$

Проанализируем полученные условия. Из (12) следует, что вектор весов, полученный в результате настройки SVM, можно записать как линейную комбинацию объектов, причем веса в этой линейной комбинации можно найти как решение двойственной задачи.

В зависимости от значений ${\xi }_i$ и ${\lambda }_i$ объекты $x_i$ разбиваются на три категории:

• ${\xi }_i=0$, ${\lambda }_i=0$. Такие объекты не влияют решение $w$ (входят в него с нулевым весом ${\lambda }_i$), правильно классифицируются (${\xi }_i=0$) и лежат вне разделяющей полосы. Объекты этой категории называются периферийными.

• ${\xi }_i=0$, $0<{\lambda }_i<C$. Из условия (15) следует, что $y_i(⟨w,x_i⟩+b)=1$, то есть объект лежит строго на границе разделяющей полосы. Поскольку ${\lambda }_i>0$, объект влияет на решение $w$. Объекты этой категории называются опорными граничными.

• ${\xi }_i>0$, ${\lambda }_i=C$. Такие объекты могут лежать внутри разделяющей полосы ($0<{\xi }_i<2$) или выходить за ее пределы (${\xi }_i\ge 2$). При этом если $0<{\xi }_i<1$, то объект классифицируется правильно, в противном случае – неправильно. Объекты этой категории называются опорными нарушителями.

Отметим, что варианта ${\xi }_i>0$, ${\lambda }_i<C$ быть не может, поскольку при ${\xi }_i>0$ из условия дополняющей нежесткости (16) следует, что ${\mu }_i=0$, и отсюда из уравнения (14) получаем, что ${\lambda }_i=C$.

Итак, итоговый классификатор зависит только от объектов, лежащих на границе разделяющей полосы, и от объектов-нарушителей (с ${\xi }_i>0$).

Построим двойственную функцию. Для этого подставим выражение (12) в лагранжиан и воспользуемся уравнениями (13) и (14) (данные три уравнения выполнены для точки минимума лагранжиана при любых фиксированных $\lambda$ и $\mu$):

$$\begin{array}{r}\begin{array}{rl}L& =\frac{1}{2}{\Vert \sum _{i=1}^{\ell }{\lambda }_i{y}_i{x}_i\Vert }^2-\sum _{i,j=1}^{\ell }{\lambda }_i{\lambda }_j{y}_i{y}_j⟨x_i,x_j⟩-b\underset{0}{\underbrace{\sum _{i=1}^{\ell }{\lambda }_i{y}_i}}+\sum _{i=1}^{\ell }{\lambda }_i+\sum _{i=1}^{\ell }{\xi }_i\underset{0}{\underbrace{(C-{\lambda }_i-{\mu }_i)}}\\ & =\sum _{i=1}^{\ell }{\lambda }_i-\frac{1}{2}\sum _{i,j=1}^{\ell }{\lambda }_i{\lambda }_j{y}_i{y}_j⟨x_i,x_j⟩.\end{array}\end{array}$$

Мы должны потребовать выполнения условий (13) и (14) (если они не выполнены, то двойственная функция обращается в минус бесконечность), а также неотрицательность двойственных переменных ${\lambda }_i\ge 0$, ${\mu }_i\ge 0$. Ограничение на ${\mu }_i$ и условие (14), можно объединить, получив ${\lambda }_i\le C$. Приходим к следующей двойственной задаче:

(18)$$\begin{array}{r}\{\begin{array}{rl}& \sum _{i=1}^{\ell }{\lambda }_i-\frac{1}{2}\sum _{i,j=1}^{\ell }{\lambda }_i{\lambda }_j{y}_i{y}_j⟨x_i,x_j⟩\to \underset{\lambda }{max}\\ & 0\le {\lambda }_i\le C,i=1,\dots ,\ell ,\\ & \sum _{i=1}^{\ell }{\lambda }_i{y}_i=0.\end{array}\end{array}$$

Она также является вогнутой, квадратичной и имеет единственный максимум.

Ядерный переход

Двойственная задача SVM (18) зависит только от скалярных произведений объектов – отдельные признаковые описания никак не входят в неё.

Note

Обратите внимание, как много это значит: решение SVM зависит только от скалярных произведений объектов (то есть похожести, если упрощать), но не от их признаковых описаний объектов. Это значит, что метод обобщается и на те случаи, когда признаковых описаний объектов нет или их получить очень дорого, но зато есть способ задать расстояние (то есть “измерить сходство”) между объектами.

Значит, можно сделать ядерный переход:

$$\begin{array}{r}\{\begin{array}{rl}& \sum _{i=1}^{\ell }{\lambda }_i-\frac{1}{2}\sum _{i,j=1}^{\ell }{\lambda }_i{\lambda }_j{y}_i{y}_{j}K(x_i,x_j)\to \underset{\lambda }{max}\\ & 0\le {\lambda }_i\le C,i=1,\dots ,\ell ,\\ & \sum _{i=1}^{\ell }{\lambda }_i{y}_i=0.\end{array}\end{array}$$

Здесь $K(x_i,x_j)$ – это функция-ядро, определенная на парах векторов, которая должна быть симметричной и неотрицательно определенной (теорема Мерсера).

Вернемся к тому, какое представление классификатора дает двойственная задача. Из уравнения (12) следует, что вектор весов $w$ можно представить как линейную комбинацию объектов из обучающей выборки. Подставляя это представление $w$ в классификатор, получаем

$$a(x)=\text{sign}(\sum _{i=1}^{\ell }{\lambda }_i{y}_i⟨x_i,x⟩+b).$$

Таким образом, классификатор измеряет сходство нового объекта с объектами из обучающей выборки, вычисляя скалярное произведение между ними. Это выражение также зависит только от скалярных произведений, поэтому в нём тоже можно перейти к ядру.

Note

Опять подчеркнем, что классификация нового примера зависит только от скалярных произведений – “похожести” нового примера на примеры из обучающей выборки, и то не все, а только опорные.

Note

В указанном выше представлении фигурирует переменная сдвига $b$, которая не находится непосредственно в двойственной задаче. Однако ее легко восстановить по любому граничному опорному объекту $x_i$, для которого выполнено ${\xi }_i=0,0<{\lambda }_i<C$. Для него выполнено $y_i(⟨w,x_i⟩+b)=1$, откуда получаем

$$b=y_i-⟨w,x_i⟩.$$

Как правило, для численной устойчивости берут медиану данной величины по всем граничным опорным объектам:

$$b=med{y}_i-⟨w,x_i⟩,{\xi }_i=0,0<{\lambda }_i<C.$$

Fig. 76 – пожалуй, самый известный рисунок в контексте SVM, он иллюстрирует ядерный трюк, в свою очередь, одну из самых красивых идей в истории машинного обучения. За счет ядерного перехода можно достигнуть линейной разделимости выборки даже в том случае, когда исходная обучающая выборка не является линейно разделимой.

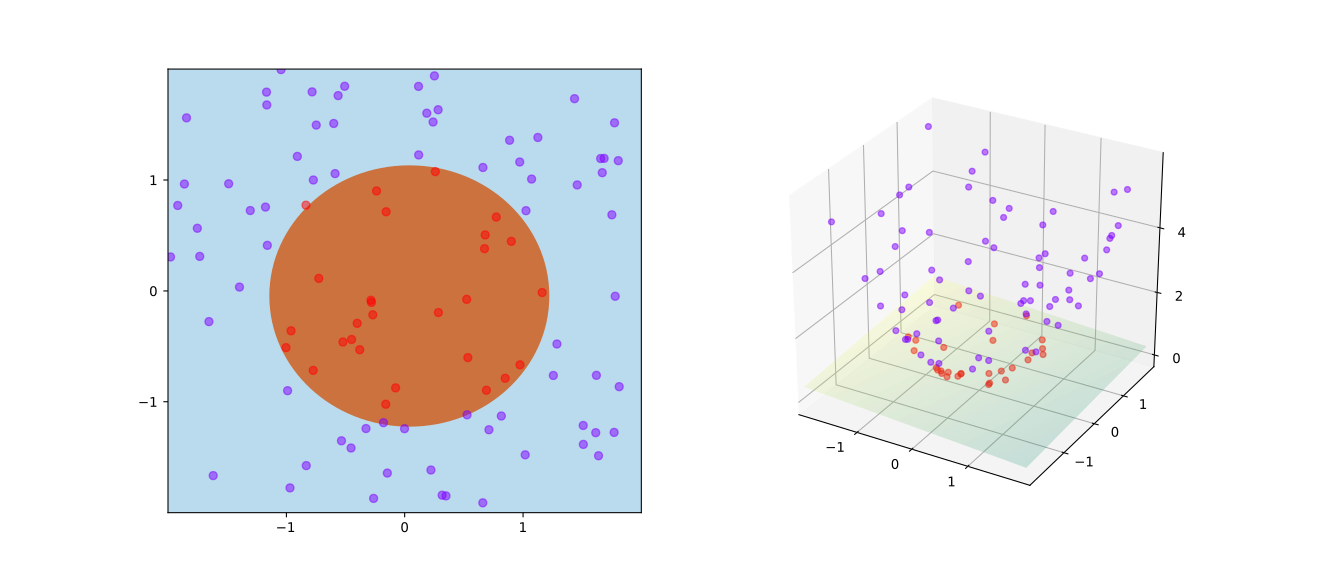
Fig. 76 Пример разделимости в новом пространстве

Наиболее часто используемые ядра:

• Линейное $K(x,y)=⟨x,y⟩$ – по сути, линейный SVM, рассмотренный выше;

• Полиномиальное ядро $K(x,y)=(⟨x,y⟩+c{)}^d$, определенное для степени ядра $d$ и параметра нормализации $c$;

• Гауссово ядро, также известное как RBF (radial-basis functions) $K(x,y)=e^{-\frac{||x-y|{|}^2}{\sigma }}$ c параметром ядра $\sigma$.

Плюсы и минусы SVM

Плюсы:

• хорошо изучены, есть важные теоретические результаты;

• красиво формулируется как задача оптимизации;

• линейный SVM быстрый, может работать на очень больших выборках;

• линейный SVM так же хорошо интерпретируется, как и прочие линейные модели;

• решение зависит только от скалярных произведений векторов, а идея “ядерного трюка” – одно из самых красивых в истории машинного обучения;

• нелинейный SVM обобщается на работу с самыми разными типами данных (последовательности, графы и т.д.) за счет специфичных ядер.

Минусы:

• нелинейный SVM имеет высокую вычислительную сложность и принципиально плохо масштабируется (оптимизационную задачу нельзя “решить на подвыборках” и как-то объединить решения);

• нелинейный SVM по сути не интерпретируется (“black box”);

• в задачах классификации часто хочется выдать вероятность отнесения к классу, SVM это не умеет делать, а эвристики, как правило, приводят к плохо откалиброванным вероятностям;

• ядерный SVM уступает специфичным нейронным сетям уже во многих задачах, например, в в приложениях к графам