Numpy#

Автор(ы):

Лукьяненко Андрей

Numpy – это широко используемая библиотека для вычислений с многомерными массивами. API большей частью вдохновлен MATLAB (великая и ужасная среда, язык и IDE для матричных вычислений), а теперь сам является примером для подражания API различных вычислительных пакетов. Более последовательный гайд стоит посмотреть на сайте библиотеки.

Массивы#

import numpy as np

a = np.array([1, 2, 3]) # создадим вектор
print(f"{a = }")

b = np.zeros((2, 2))
print(f"{b = }")

c = np.eye(3)
print(f"{c = }")

q = np.random.random((1, 20))
print(f"{q = }")

a = array([1, 2, 3])
b = array([[0., 0.],
       [0., 0.]])
c = array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]])
q = array([[0.53151625, 0.00934893, 0.97626252, 0.92762173, 0.83292922,
        0.79171128, 0.79835923, 0.26750344, 0.89347767, 0.65369853,
        0.82280163, 0.82373965, 0.49174471, 0.34821123, 0.14480575,
        0.61324825, 0.6170773 , 0.44544968, 0.8563237 , 0.36692683]])

Арифметические операции#

Для удобства использования np.ndarray арифметические операторы определены так, чтобы соответствовать ожиданиям:

a = np.array([1, 2, 3])
b = np.array([-1, 3, 4])

diff = a - b
print(f"{diff = }")

mult = a * b
print(f"{mult = }")

scalar_mult = a @ b
print(f"{scalar_mult = }")

diff = array([ 2, -1, -1])
mult = array([-1,  6, 12])
scalar_mult = 17

Indexing, slicing and sugar#

Numpy поддерживает, кажется, все разумные варианты индексации:

a = np.arange(16).reshape(4, 4)
print(f"{a = }")

# просто по индексам
print(f"\n{a[0, 1] = }")
print(f"{a[0][1] = }")

# по слайсам
print(f"\n{a[0, 1:3] = }")
print(f"{a[2] = }")
print(f"{a[2, :] = }")
print(f"{a[2, ...] = }")

# по маске
mask = (a % 3 == 0)
print(f"\n{mask = }")
print(f"{a[mask] = }")

first_rows = np.array([True, True, False, False])
print(f"\n{a[first_rows] = }")

a = array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])

a[0, 1] = 1
a[0][1] = 1

a[0, 1:3] = array([1, 2])
a[2] = array([ 8,  9, 10, 11])
a[2, :] = array([ 8,  9, 10, 11])
a[2, ...] = array([ 8,  9, 10, 11])

mask = array([[ True, False, False,  True],
       [False, False,  True, False],
       [False,  True, False, False],
       [ True, False, False,  True]])
a[mask] = array([ 0,  3,  6,  9, 12, 15])

a[first_rows] = array([[0, 1, 2, 3],
       [4, 5, 6, 7]])

Для работы с размерностями часто используются еще три конструкции: None, ... (ellipsis, многоточие) и : (двоеточие).

a = np.arange(16).reshape(4, 4)
print(f"{a = }")

# None добавляет ось размерности 1
print(f"\n{a[None].shape = }")
print(f"{a[:, :, None].shape = }")

# : превращается в slice (None), берет все элементы вдоль размерности
print(f"\n{a[2, :] = }")
print(f"{a[2, 0:None] = }")

# ... ellipsis, превращается в необходимое число двоеточий :,:,:
print(f"\n{a[...] = }")

# также ... удобен когда мы не знаем настоящий шейп массива или нужно не трогать несколько подряд идущих размерностей
z = np.arange(27).reshape(3, 3, 3)
print(f"\n{z[0, ..., 1] = }")
print(f"{z[0, :, 1] = }")

a = array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])

a[None].shape = (1, 4, 4)
a[:, :, None].shape = (4, 4, 1)

a[2, :] = array([ 8,  9, 10, 11])
a[2, 0:None] = array([ 8,  9, 10, 11])

a[...] = array([[ 0,  1,  2,  3],
       [ 4,  5,  6,  7],
       [ 8,  9, 10, 11],
       [12, 13, 14, 15]])

z[0, ..., 1] = array([1, 4, 7])
z[0, :, 1] = array([1, 4, 7])

В целом в NumPy очень здорово реализованы методы __getitem__/__setitem__.

a = np.array([1, 2, 3])
element = a[2]
print(f"{element = }")

a[2] = 5
print(f"{a = }")

element = 3
a = array([1, 2, 5])

Кроме того, мы можем делать индексацию по заданному условию с помощью np.where.

# создадим вектор
a = np.array([2, 4, 6, 8])

selection = np.where(a < 5)
print(f"{selection = }")

# дополнительно можем передать два значения или вектора, при выполнении условия выбираются элементы из первого значения/вектора, при невыполнении -- из второго
a2 = np.where(a < 5, 2, a * 2)
print(f"{a2 = }")

# np.where работает и с многомерными массивами
b = np.array([[8, 8, 2, 6], [0, 5, 3, 4]])
b_mult = np.where(b < 4, b, 1)
print(f"{b_mult = }")

selection = (array([0, 1]),)
a2 = array([ 2,  2, 12, 16])
b_mult = array([[1, 1, 2, 1],
       [0, 1, 3, 1]])

Broadcasting#

Что происходит, если мы хотим производить арифметические операции с массивами разных размеров?

a = np.array([1, 2, 3])
k = 2
broad = a * k
print(f"{broad = }")

broad = array([2, 4, 6])

С точки зрения математики, ничего интересного тут не происходит: мы подразумевали умножение всего вектора на скаляр. Однако матричные операции в numpy справляются и с менее очевидными случаями, например, при сложении или вычитании вектора и скаляра:

a = np.array([1, 2, 3])
k = 2
broad = a - k
print(broad)

[-1  0  1]

В numpy приняты следующие правила работы с массивами разного размера:

размерности сравниваются справа налево;
два массива совместимы в размерности, если она одинаковая, либо у одного из массивов единичная;
вдоль отсутствующих размерностей происходит расширение повторением (np.repeat).

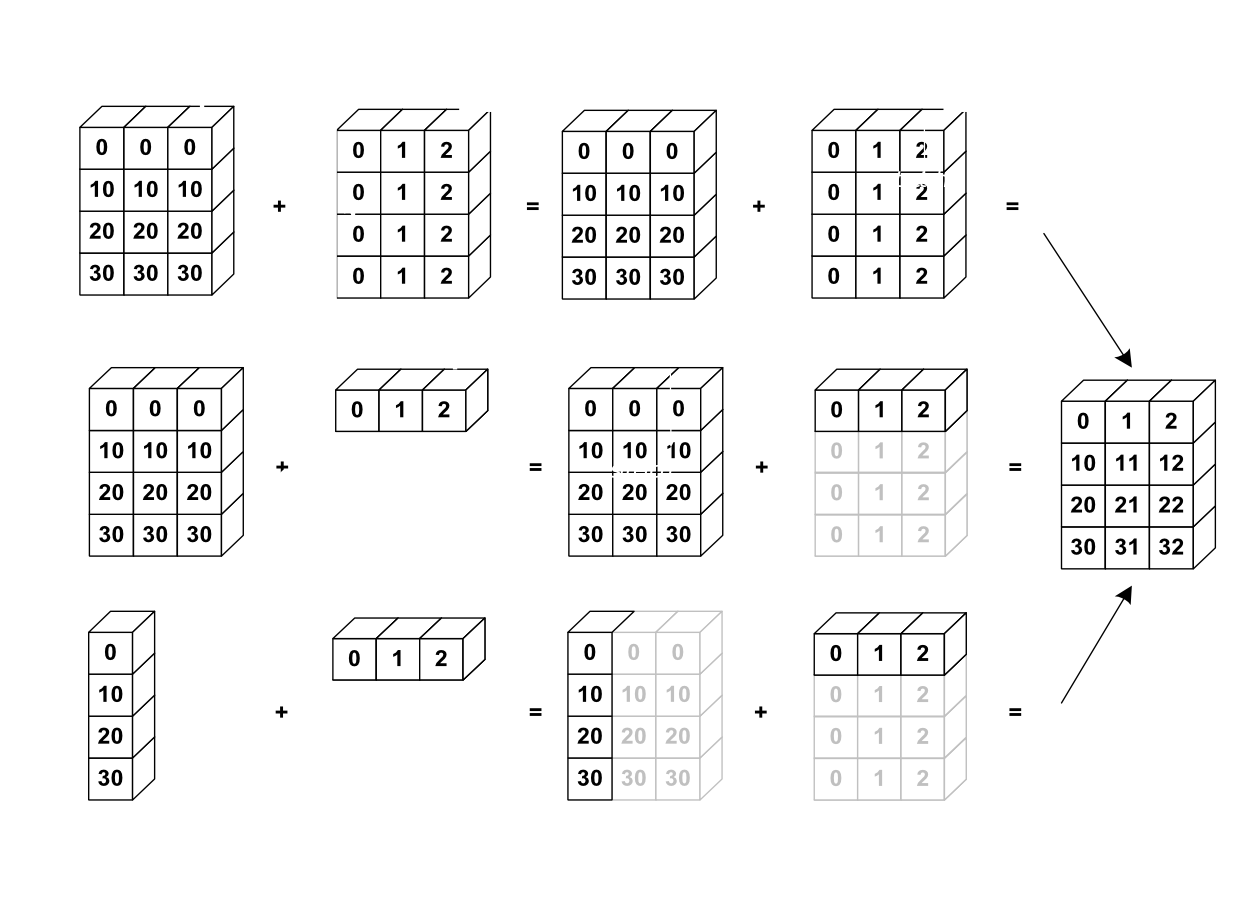
../../../_images/numpy_work_with_arrays.png

Attention

Be aware Автоматический броадкастинг легко приводит к ошибкам, так что лучше делать его самостоятельно в явной форме.

Операции с плавающей точкой#

Отдельно стоит поговорить про числа с плавающей точкой. Число с плавающей точкой (или число с плавающей запятой) – экспоненциальная форма представления вещественных (действительных) чисел, в которой число хранится в виде мантиссы и порядка (показателя степени). При этом число с плавающей точкой имеет фиксированную относительную точность и изменяющуюся абсолютную. В результате одно и то же значение может выглядеть по-разному, если хранить его с разной точностью.

f16 = np.float16("0.1")
f32 = np.float32(f16)
f64 = np.float64(f32)
print(f"{f16 = }, {f32 = }, {f64 = }")
print(f"{f16 == f32 == f64 = }")

f16 = np.float16("0.1")
f32 = np.float32("0.1")
f64 = np.float64("0.1")
print(f"{f16 = }, {f32 = }, {f64 = }")
print(f"{f16 == f32 == f64 = }")

f16 = 0.1, f32 = 0.099975586, f64 = 0.0999755859375
f16 == f32 == f64 = True
f16 = 0.1, f32 = 0.1, f64 = 0.1
f16 == f32 == f64 = False

Из-за этого для сравнения массивов с типом float используют np.allclose.

print(f"{np.allclose([1e10,1e-7], [1.00001e10,1e-8]) = }")
print(f"{np.allclose([1e10,1e-8], [1.00001e10,1e-9]) = }")

np.allclose([1e10,1e-7], [1.00001e10,1e-8]) = False
np.allclose([1e10,1e-8], [1.00001e10,1e-9]) = True

NumPy и линейная алгебра#

В Numpy много удобных функций, которые позволяют упростить код. Приведем несколько примеров:

# матрица с единицами по диагонали и с нулями в остальных ячейках
print(f"{np.eye(2, dtype=int) = }")
# есть возможность указать индекс диагонали
print(f"{np.eye(3, k=-1, dtype=int) = }")

# в Numpy есть свой генератор случайных чисел и векторов
print(f"{np.random.beta(1, 2) = }")
print(f"{np.random.randint(1, 5, (2, 3)) = }")

# Numpy позволяет заменить значений основной диагонали матрицы.
# внимание, эта функция работает in-place
a = np.random.randint(1, 5, (3, 3))
print(f"{a = }")
np.fill_diagonal(a, 4)
print(f"{a = }")

# Можно сделать и наоборот -- получить вектор значений диагонали матрица
print(f"{np.diag(a) = }")

np.eye(2, dtype=int) = array([[1, 0],
       [0, 1]])
np.eye(3, k=-1, dtype=int) = array([[0, 0, 0],
       [1, 0, 0],
       [0, 1, 0]])
np.random.beta(1, 2) = 0.5837805924179247
np.random.randint(1, 5, (2, 3)) = array([[1, 2, 3],
       [4, 2, 2]])
a = array([[4, 1, 1],
       [2, 2, 3],
       [2, 4, 1]])
a = array([[4, 1, 1],
       [2, 4, 3],
       [2, 4, 4]])
np.diag(a) = array([4, 4, 4])

Решение систем линейных уравнений#

Numpy позволяет решить систему линейных уравнений.

a = np.array([[7, 4], [9, 8]])
b = np.array([5, 3])
solution = np.linalg.solve(a, b)
print(solution)

[ 1.4 -1.2]

Обращение матриц#

Numpy дает возможность выполнить операцию обращения матриц.

a = np.array([[1., 2.], [3., 4.]])
inv = np.linalg.inv(a)
print(inv)

[[-2.   1. ]
 [ 1.5 -0.5]]

Собственные вектора и числа#

Вычисление собственных векторов и чисел.

print(np.linalg.eig(np.diag((1, 2, 3))))

(array([1., 2., 3.]), array([[1., 0., 0.],
       [0., 1., 0.],
       [0., 0., 1.]]))

Мы вкратце рассмотрели#

основы работы с NumPy;
индексацию в массивах;
broadcasting массивов NumPy;
операции с плавающей точкой;
NumPy и примитивы линейной алгебры.

QMLCourse

Numpy

Contents

Numpy#

Массивы#

Арифметические операции#

Indexing, slicing and sugar#

Broadcasting#

Операции с плавающей точкой#

NumPy и линейная алгебра#

Решение систем линейных уравнений#

Обращение матриц#

Собственные вектора и числа#

Мы вкратце рассмотрели#