Модель Изинга#

Автор(ы):

В этой лекции познакомимся с моделью Изинга, которая изначально была разработана для описания магнетизма, но оказалась настолько удачной и универсальной, что сегодня к решению именно этой задачи стараются свести многие проблемы реального мира, причем не только из физики. В следующем блоке подробно покажем, как к гамильтонианам типа Изинга, или, по-другому, “спиновым стеклам” могут быть сведены задачи комбинаторной оптимизации и квантовой химии. Так что знакомство с этой удивительной моделью, а также описывающим ее гамильтонианом нам просто необходимо!

Note

Специальные квантовые компьютеры компании D-Wave сконструированы так, что они могут решать вообще только одну задачу – нахождения основного состояния гамильтонианов типа Изинга. Но эта задача настолько распространена и важна, что эти компьютеры стали первыми в мире коммерческими квантовыми компьютерами! Кстати, далее этим компьютерам у нас посвящена отдельная лекция.

Ближайшее время посвятим довольно много времени объяснению этой модели. Это может показаться скучным и занудным, но это важно для понимания того, как это все работает и как решать с помощью вариационных квантовых алгоритмов реальные задачи!

Задача Изинга в одномерном случае#

Note

Ниже попробуем на пальцах объяснить модель Изинга. Пробовать будем через цепочку атомов антиферромагнетика во внешнем магнитном поле. Ели вы плохо помните физику и вам это объяснение покажется сложным, то не расстраивайтесь – дальше также объясним задачу Изинга как задачу о поиске максимального разреза в графе – известную задачу комбинаторной оптимизации.

Пусть у нас есть, например, цепочка атомов, которые обладают магнитным моментом. Например, цепочка атомов антиферромагнетика. И мы прикладываем к этой цепочке внешнее магнитное поле.

Тогда, если поле маленькое, наши атомы будут стараться выстроиться в антиферромагнитный порядок, когда соседние из них имеют моменты, направленные в разные стороны. Но если поле уже большое, то оно будет стремиться “повернуть” моменты по своему направлению. А если еще вспомнить, что магнитный момент атома является квантовой величиной и может быть в суперпозиции состояний в одну сторону и в противоположную, то не очень маленькое, но и не слишком большое поле будет переводить часть атомов именно в такие суперпозиции.

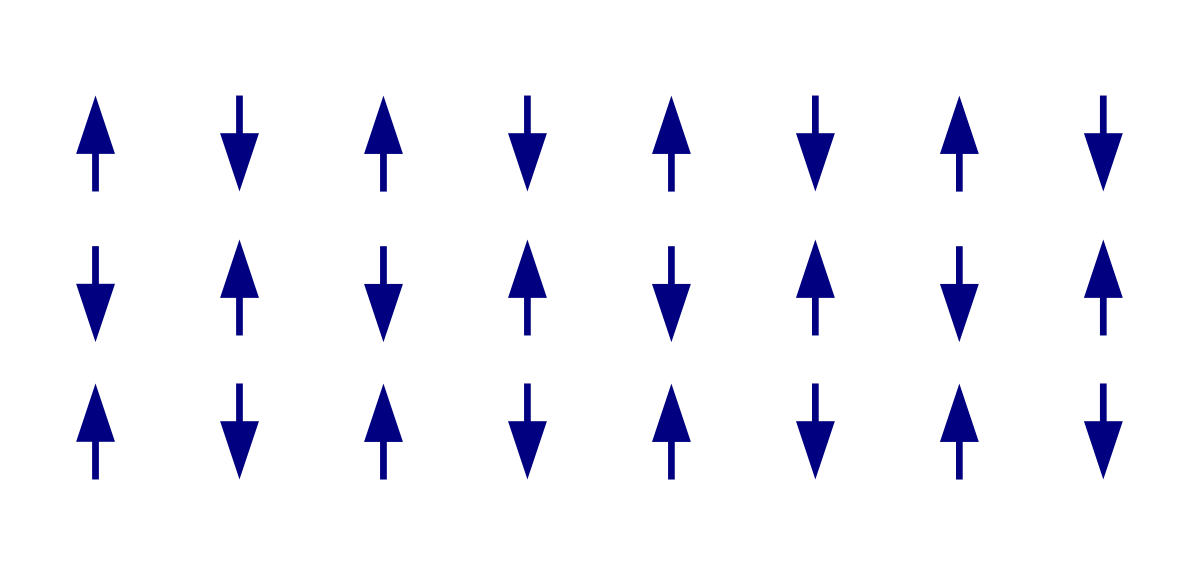
../../../_images/af_ordering.png

Fig. 85 Иллюстрация антиферромагнитного порядка#

Reminder о квантовой физике

В квантовой механике есть фундаментальное уравнение, которое описывает динамику квантовых систем. Оно называется уравнением Шредингера: \(\imath \hbar \frac{\partial \Psi}{\partial t} = \hat{H} \Psi\), где \(\hat{H}\) – это оператор Гамильтона, или гамильтониан. Также его называют оператором полной энергии системы, так как в общем случае он равен сумме операторов кинетической и потенциальной энергии. Начиная с этой лекции будем очень часто обращаться к этому оператору, но в целом в нем нет ничего принципиально сложного. Это такой же эрмитов оператор, как и другие. А наблюдаемая величина, которую получаем при измерении этого оператора – это энергия системы.

Давайте теперь запишем гамильтониан такой системы. Для представления магнитных моментов будем использовать оператор \(\sigma^z\) – другими словами, спин в направлении оси \(Z\). Если кто-то забыл, как выглядит оператор \(\sigma^z\), то рекомендуем еще раз просмотреть раздел про операторы Паули первой лекции. Далее будем очень активно использовать эти матрицы для представления задач реального мира!

Для начала, в случае если внешнего поля нет, мы должны записать взаимодействие соседних атомов. Так как у нас антиферромагнетик, минимальная энергия достигается в случае, если каждый спин противонаправлен с соседними. Это просто оператор \(\sigma^z_j \sigma^z_{j+1}\), который действует на все пары соседних спинов. Ну и сразу введем некоторую константу обменного взаимодействия \(J\), чтобы потом нам было удобно сравнивать ее с внешним полем. В итоге, для цепочки из \(N\) спинов, получаем:

\[ \hat{H}_{h=0} = J \sum_{i=0}^{N-1} \sigma^{z}_i \sigma^{z}_{i+1} \]

А теперь давайте добавим внешнее поле \(h\). В этом случае поле просто действует на все спины и пытается выстроить их в зависимости от своего направления, например, вниз. Тогда полный гамильтониан такой системы можно записать в виде:

\[ \hat{H}_{h\neq 0} = J \sum_{i=0}^{N-1} \hat{\sigma}^{z}_i\hat{\sigma}^{z}_{i+1} - h\sum_{i=0}^N \hat{\sigma}^{z}_i \]

Задача Изинга как задача о максимальном разрезе в графе#

Задача о максимальном разрезе в графе – это очень известная задача комбинаторики. Она относится к классу \(NP\)-трудных, и к ней можно свести все другие \(NP\) задачи. При этом ее формулировка одна из самых простых среди всего класса задач. Формулируется она следующим образом.

Нам дан граф – набор вершин \(V\) и связывающих их ребер \(E\). Нам надо найти такое разделение вершин \(V\) на два непересекающихся набора \(V_1, V_2\), что число ребер между вершинами из разных наборов будет максимально.

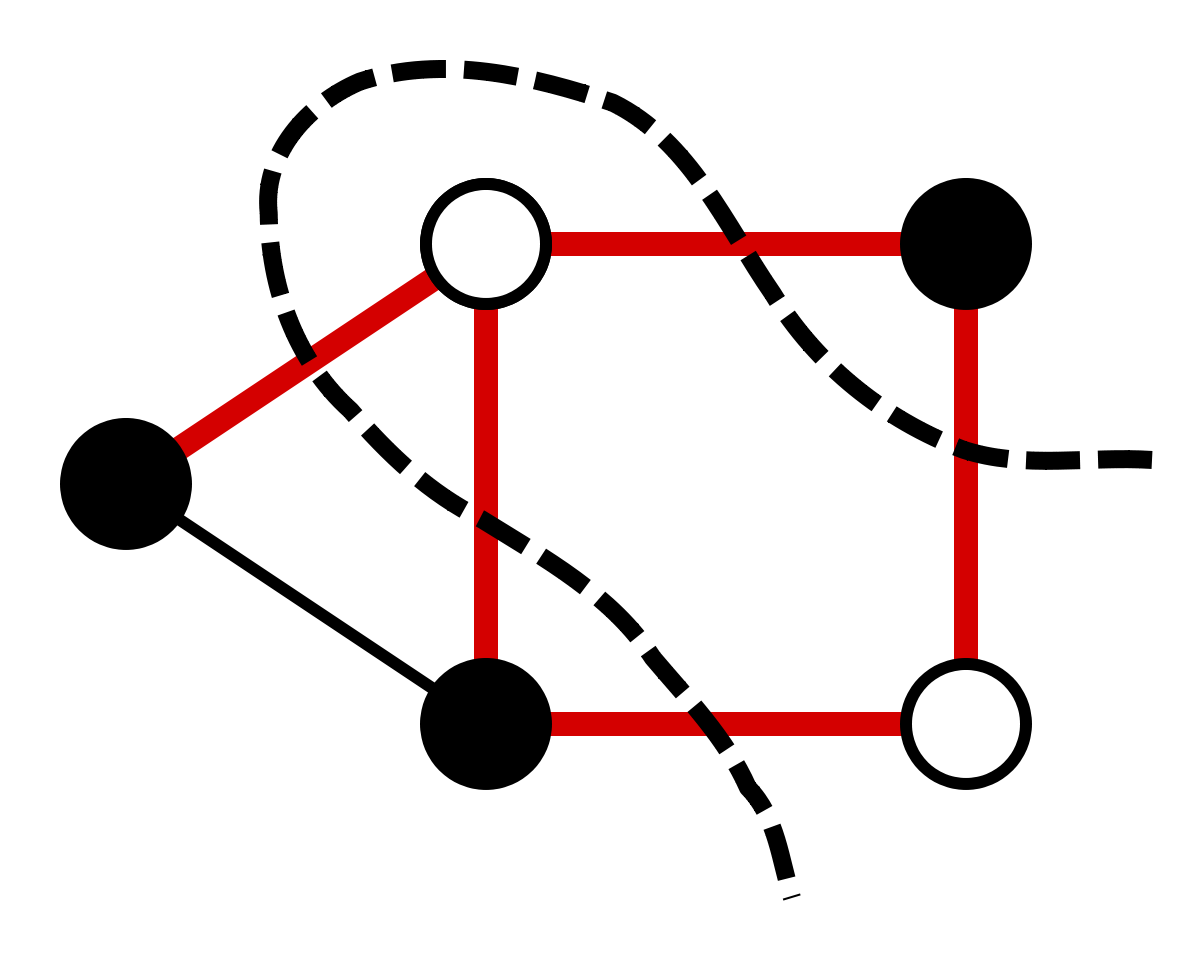
../../../_images/Max-cut.png

Fig. 86 Иллюстрация задачи о максимальном разрезе в графе#

Теперь давайте представим, что каждой вершине нашего графа сопоставили кубит. Для этих кубитов можем производить измерения по оси \(Z\), чтобы понять, как направлен тот или иной спин. И давайте запишем вот такой гамильтониан и внимательно на него посмотрим:

\[ \hat{H} = \sum_{u,v \in E} \hat{\sigma}^z_u \hat{\sigma}^z_v \]

Тут суммирование \(u,v \in E\) идет по всем ребрам графа, а \(u,v\) – вершины инцидентные ребрам. Если вспомнить, что собственные значения \(\sigma^z\) это \(\pm 1\) для, соответственно, спина “вверх” и спина “вниз”, то не трудно понять, в каком случае у нас будет минимум энергии этого гамильтониана. А будет он тогда, когда максимальное число пар вершин \(u,v\) имеют разную ориентацию своих спинов. Ведь если они имеют одинаковую направленность (причем не важно, \(+1\) или \(-1\)), их произведение будет равно \(1\), но если направленность разная, то их произведение даст нам \(-1\). Таким образом, минимум энергии такого гамильтониана достигается тогда, когда мы разбили наши вершины на две группы – спин “вверх” и спин “вниз” – причем число ребер между этими группами максимальное. А это в чистом виде формулировка задачи о максимальном разрезе в графе!

Note

Тематика квантовой физики мало обсуждалась в первых лекциях, но нам пока достаточно знать лишь то, что для любая физическая система (включая квантовую) стремится в состояние с минимальной энергией. Например, тело, подброшенное вверх, стремится упасть на землю, а возбужденный атом стремится релаксировать в невозбужденное состояние.

При этом из квантовой физики помним, что для реальных физических систем наиболее вероятными являются состояния с минимальной энергии и системы стремятся в эти состояния прийти. Теперь для простоты предположим, что наш граф – это просто цепочка, то есть ребра есть лишь между соседними в одномерном пространстве вершинами. Ну и теперь давайте сформулируем нашу задачу о максимальном разрезе чуточку сложнее – нам надо найти не просто максимальный разрез, а такой разрез, который самый большой при наименьшем числе вершин в наборе \(V_1\). И поскольку теперь у нас два вклада в стоимость, то нам нужны коэффициенты, которые покажут, что важнее. Пусть это будут \(J\) и \(h\). Тогда гамильтониан соответствующей модели Изинга можно записать так:

\[ \hat{H} = J \sum_{i=0}^{N-1} \hat{\sigma}^{z}_i\hat{\sigma}^{z}_{i+1} - h\sum_{i=0}^N \hat{\sigma}^{z}_i \]

Как видно, это тот же самый гамильтониан, который получили и для моделирования антиферромагнетиков. То есть задача об основном состоянии цепочки антиферромагнитных частиц во внешнем поле эквивалентна задаче о максимальном разрезе в графе-цепочке при некотором штрафе за одно из выделенных направлений спинов. Эквивалентность в данном случае значит, что:

  • решив задачу о максимальном разрезе, можно найти и основное состояние физической системы;

  • как-то смоделировав физическую систему, подождав пока она релаксирует, после чего измерив ее, получим конфигурацию, отвечающую решению задачи о максимальном разрезе.

Note

Одномерная цепочка атомов, или поиск максимального разреза в графе-цепочке, является простым случаем и не является \(NP\)-задачей. Однако уже в двумерном случае эта задача становится сильно сложнее, как и, например, если в цепочке атомов ферромагнетика добавим взаимодействие не только соседних спинов, но и взаимодействие с соседями соседа. Аналогично, модель вида Изинга сильно усложняется при добавлении недиагональных (off-diagonal elements) элементов гамильтониана, например, когда внешнее поле направлено в другом направлении и второй член гамильтониана принимает вид \(h\sum_{i=N} \sigma^{x}_i\). Более подробное исследование данной модели приводится в этой продвинутой лекции.

Модель Изинга на чистом NumPy#

Давайте попробуем реализовать одномерный гамильтониан Изинга на чистом NumPy/SciPy в виде разреженной матрицы. Для этого вспомним, что действуя оператором \(\sigma^z\) на \(i\)-й кубит, одновременно действуем единичным оператором на все остальные, а потом перемножаем все операторы произведением Кронекера. Из лекций по линейной алгебре помним также об ассоциативности произведения Кронекера, чем и воспользуемся:

import numpy as np
from scipy import sparse
from scipy.sparse import linalg as sl

def sigmaz_k(k: int, n: int) -> (sparse.csr_matrix):
    left_part = sparse.eye(2 ** k)
    right_part = sparse.eye(2 ** (n - 1 - k))

    return sparse.kron(
        sparse.kron(
            left_part,
            sparse.csr_matrix(np.array([[1, 0,], [0, -1,],]))
        ),
        right_part
    )

А теперь можем реализовать и сам оператор Изинга:

def ising(j: float, h: float, n: int) -> (sparse.csr_matrix):
    res = sparse.csr_matrix((2 ** n, 2 ** n), dtype=np.complex64)

    for i in range(n - 1):
        res += j * sigmaz_k(i, n) * sigmaz_k(i + 1, n)
        res -= h * sigmaz_k(i, n)

    res -= h * sigmaz_k(n - 1, n)

    return res

Если внешнего поля нет, спины выстраиваются в полный антиферромагнитный порядок, в чем легко убедиться. Создадим оператор для такой модели и, например, 10 спинов (или 10 вершин в графе, если говорим в терминах Max-Cut):

op = ising(1, 0, 10)
solution = sl.eigs(op, which="SR", k=1, return_eigenvectors=True)
print(f"Energy: {solution[0][0]}")

Energy: (-9.000000000000018-2.208468631860285e-16j)

Note

Тут пользуемся функциями из ARPACK – набором рутин для линейной алгебры разреженных систем. Более подробно о способах и алгоритмах классических решений задачи о собственных значениях расскажем в одной из следующих лекций, полностью посвещнной этой теме. Пока же просто используем эту рутину как “черный ящик”. Более подробное описание этой функции и ее аргументов можно посмотреть в документации библиотеки SciPy.

Эта энергия соответствует антиферромагнитному порядку, в этом легко убедиться, нарисовав спины и формулу на бумажке. Внимательный читатель заметил, что в этот раз вернули также и первый собственный вектор, который в нашем случае является волновой функцией основного состояния. А как знаем, квадраты элементов вектора волновой функции дают нам вероятности соответствующих битовых строк (если для вас это все звучит дико, то очень рекомендуем вернуться к лекции про кубит). Давайте посмотрим на эту битовую строку, иначе на порядок наших спинов в решении (или на разбиение вершин графа на два подмножества в терминах Max-Cut):

def probs2bit_str(probs: np.array) -> (str):
    size = int(np.log2(probs.shape[0]))
    bit_s_num = np.where(probs == probs.max())[0][0]

    s = f"{bit_s_num:b}"
    s = "0" * (size - len(s)) + s

    return s

probs = solution[1] * solution[1].conj()
print(probs2bit_str(probs))

0101010101

Теперь давайте попробуем добавить внешнее поле с коэффициентом, равным удвоенному значению константы обменного взаимодействия. В терминах комбинаторной задачи, добавляем штраф, равный \(2\) умножить на число спинов, направленных вверх.

def external_field(j: float, h: float, n: int) -> (None):
    op = ising(j, h, n)
    solution = sl.eigs(op, which="SR", k=1, return_eigenvectors=True)
    print(f"Energy: {solution[0][0]}")

    probs = solution[1] * solution[1].conj()
    print(probs2bit_str(probs))

external_field(1, 2, 10)

Energy: (-10.99999999999999-1.0571225056728771e-16j)
0101010010

Видим, что теперь наш антиферромагнитный порядок уже не полный. В целом, данная модель довольно интересная, так как при некотором отношении \(\frac{h}{J}\) у нас происходит фазовый переход от полной упорядоченности, а при дальнейшем росте \(h\) приходим к одинаковой ориентации всех спинов, в чем легко убедиться, взяв, например, \(h = 100\):

external_field(1, 100, 10)

Energy: (-991.0000000000039-3.4882612571137096e-14j)
0000000000

Заключение#

В этой лекции на базовом уровне познакомились с моделью Изинга – очень важным концептом в квантовом машинном обучении. Узнали, что:

  • модель Изинга изначально была создана для объяснения магнетизма;

  • нахождение решений для модели Изинга в общем случае – \(NP\)-полная задача;

  • модель Изинга также может быть сформулирована в терминах задачи о максимальном разрезе в графе (и наоборот);

  • в классической модели Изинга существуют интересные фазовые переходы;

  • модель Изинга легко реализовать в коде, используя SciPy, но размерность задачи растет очень быстро.