QUBO-формулировки для линейной регрессии, SVM и метода k-средних

Автор(ы):

• Бурдейный Дмитрий

Описание лекции

Здесь рассмотрим QUBO-формулировки трех задач ML (линейная регрессия, SVM, сбалансированная кластеризация методом k-средних) аналогично тому, как в предыдущей лекции было продемонстрировано сведение к QUBO задач о максимальном разрезе в графе, о коммивояжере и о выделении сообществ в графе. Изложение полностью основывается на статье [DAPN21].

Некоторые обозначения, которые будут использоваться в дальнейшем:

• $\mathbb{R}$ – множество действительных чисел;

• $N$ – количество объектов в обучающем наборе, $N\in \{1,2,\dots \}$;

• $d$ – количество признаков (features) для объектов в обучающем наборе, $d\in \{1,2,\dots \}$;

• $X$ – тренировочный набор, содержит по одному объекту в каждой из $N$ строк, каждая строка содержит $d$ значений признаков, $X\in {\mathbb{R}}^{N\times d}$;

• $Y$ – набор истинных “ответов” (ground truth), соответствующих тренировочным объектам из $X$ ($Y\in {\mathbb{R}}^N$ в случае регрессии, $Y\in \{0,1{\}}^N$ в случае бинарной классификации);

• $\otimes$ – произведение Кронекера (тензорное произведение);

• $\odot$ – произведение Адамара (поэлементное произведение).

Общая формулировка QUBO-задачи, которая используется в статье [DAPN21] и к которой всё сводится, выглядит так:

(47)$$z^{T}Az+z^{T}b\to \underset{z\in \{0,1{\}}^M}{min}$$

где $M$ – натуральное число, $z$ – бинарный вектор решения, $A\in {\mathbb{R}}^{M\times M}$ – QUBO-матрица с действительными элементами, $b\in {\mathbb{R}}^M$ – QUBO-вектор. Как отмечалось в предыдущей лекции, при $z_i\in \{0,1\}$ выполняется равенство $z_i^2=z_i$, так что линейные члены в (47) можно включить в квадратичные, но этого делать не будем, т.к. для целей этой лекции и для лучшего понимания удобнее сохранить минимизируемую квадратичную форму именно в виде (47).

Линейная регрессия

В задаче линейной регрессии предполагается, что зависимость истинных ответов от признаков тренировочных объектов приближенно линейная:

$$y_i^{(pred)}=⟨w,x_i⟩+b,y_i^{(pred)}\approx y_i,$$

где $y_i^{(pred)}$ – предсказываемое значение, $y_i$ – истинное значение (из разметки), $⟨\cdot ,\cdot ⟩$ – скалярное произведение. Удобно сразу избавиться от слагаемого $b$ (bias), добавив единицу к набору признаков. Тогда bias окажется включенным в веса $w$, а тренировочный набор будет иметь по $(d+1)$ признаков на объект: $X\in {\mathbb{R}}^{N\times (d+1)}$. Требуется найти веса $w$, при которых квадрат евклидовой нормы невязки минимален:

(48)$$E(w)=||Xw-Y|{|}^2\to \underset{w\in {\mathbb{R}}^{d+1}}{min}$$

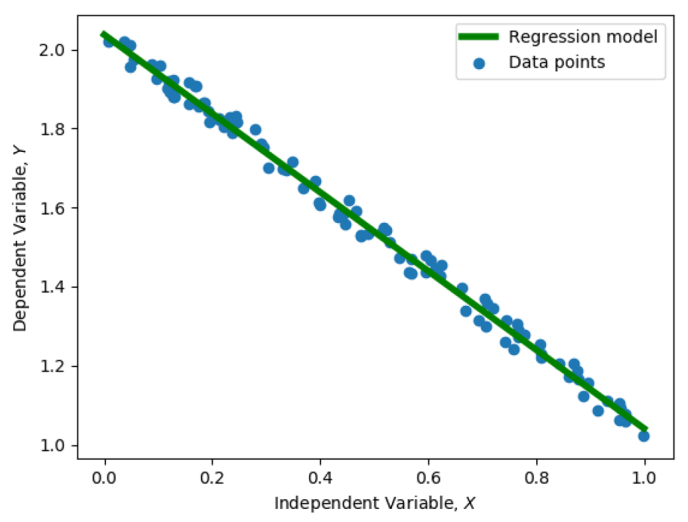
Fig. 94 Иллюстрация к задаче линейной регрессии.

Известно аналитическое решение задачи (48):

$$w={\left(X^{T}X\right)}^{-1}{X}^{T}Y$$

Если ${\left(X^{T}X\right)}^{-1}$ не существует, нужно вычислить псевдообратную матрицу. ВременнАя сложность решения задачи линейной регрессии равна $\mathcal{O}(N{d}^2)$, т.к. нужно $\mathcal{O}(N{d}^2)$ для вычисления матрицы $X^{T}X$ и $\mathcal{O}(d^3)$ для вычисления обратной к ней (предполагаем, что $N\gg d$).

QUBO-формулировка

Перепишем выражение (48):

(49)$$E(w)=w^T{X}^{T}Xw-2w^T{X}^{T}Y+Y^{T}Y\to \underset{w\in {\mathbb{R}}^{d+1}}{min}$$

Наша цель – найти вектор $w$, компоненты которого – действительные числа. Но в QUBO-формулировке необходимо представить решение в виде вектора с бинарными компонентами. Как это сделать? Конечно, напрашивается идея использовать бинарное представление действительного числа $w_i$ (будем отдельно записывать в бинарном виде целую часть, отдельно – дробную). Нужно помнить о том, что знак $w_i$ может быть как положительным, так и отрицательным. Формат представления придется выбрать фиксированным (т.е. с фиксированной запятой, не с плавающей запятой). Пример:

$$\begin{array}{r}\begin{array}{rl}\pm 110.101& =\pm \underset{\text{идем влево от разд. точки}}{\underbrace{(0\cdot 2^0+1\cdot 2^1+1\cdot 2^2)}}\pm \underset{\text{идем вправо от разд. точки}}{\underbrace{(1\cdot 2^{-1}+0\cdot 2^{-2}+1\cdot 2^{-3})}}\\ & =\pm (2+4+\frac{1}{2}+\frac{1}{8})\\ & =\pm 6.625\end{array}\end{array}$$

Бинарные компоненты логично рассматривать как индикаторы наличия или отсутствия соответствующих степеней двойки в бинарном представлении каждого действительного числа. Введем вектор-столбец $P$, который отвечает за точность представления (Precision vector) и состоит из степеней двойки со знаками:

$$P={[-2^l,-2^{l-1},\dots ,-2^{-m+1},-2^{-m},2^{-m},2^{-m+1},\dots ,2^{l-1},2^l]}^T,$$

этот вектор отсортирован по возрастанию элементов. Отводится $l$ двоичных разрядов для целой части числа, $m$ разрядов для дробной. $l$ определяется максимальным по модулю действительным числом, которое хотим представлять; $m$ определяется желаемой точностью представления. Число элементов вектора $P$ равно $(m+1+l)\cdot 2=K$.

Вводим вектор ${\tilde{w}}_i\in \{0,1{\}}^K$ такой, что

$${\tilde{w}}_i^{T}P=\sum _{k=1}^K{p}_k{\tilde{w}}_{ik}\approx w_i\in \mathbb{R}$$

Чтобы не было неоднозначности, нужно договориться о том, что для представления $w_i>0$ используем только положительные элементы вектора $P$, а для $w_i<0$ – только отрицательные.

Составляем бинарный вектор $\tilde{w}\in \{0,1{\}}^{K(d+1)}$

$$\tilde{w}=[\underset{\text{предст. }{w}_1}{\underbrace{{\tilde{w}}_{11}\dots {\tilde{w}}_{1K}}}\underset{\text{предст. }{w}_2}{\underbrace{{\tilde{w}}_{21}\dots {\tilde{w}}_{2K}}}\dots \underset{\text{предст. }{w}_{d+1}}{\underbrace{{\tilde{w}}_{(d+1)1}\dots {\tilde{w}}_{(d+1)K}}}{]}^T$$

и матрицу точности $\mathcal{P}$ (Precision matrix), которая задает переход к бинарному представлению векторов:

$$\mathcal{P}=I_{d+1}\otimes P^T,$$

где $I_{d+1}$ – единичная матрица размера $(d+1)$. Матрица $\mathcal{P}$ имеет размерность $(d+1)\times K(d+1)$. Исходный вектор весов можно записать как

(50)$$w=\mathcal{P}\tilde{w},$$

где знак “=” на самом деле означает приближенное равенство (наше fixed-point представление имеет конечную точность).

Всё готово для того, чтобы переписать исходную задачу (49) в QUBO-формулировке. Подставляем (50) в (49) и получаем

(51)$$E(\tilde{w})={\tilde{w}}^T{\mathcal{P}}^T{X}^{T}X\mathcal{P}\tilde{w}-2{\tilde{w}}^T{\mathcal{P}}^T{X}^{T}Y\to \underset{\tilde{w}\in \{0,1{\}}^{(d+1)K}}{min}$$

слагаемое $Y^{T}Y$ отброшено, т.к. это константа, никак не влияющая на решение задачи оптимизации без ограничений.

Оценка вычислительной сложности

Для исходной задачи регрессии (48) количество значений в датасете $X$ равно $\mathcal{O}(Nd)$. Мы ввели $K$ бинарных переменных для каждого из $(d+1)$ весов. Значит, получилось $\mathcal{O}(Kd)$ переменных в QUBO-формулировке (51). Для решения задачи требуется $\mathcal{O}(K^2{d}^2)$ кубитов (см. [DPP19]), это пространственная сложность в рассматриваемом подходе.

ВременнАя сложность в классической задаче $\mathcal{O}(N{d}^2)$. В случае QUBO-задачи для временнОй оценки нужно рассмотреть три части:

1. Затраты времени для конвертации задачи регрессии в QUBO-формулировку. Здесь получаем $\mathcal{O}(N{K}^2{d}^2)$ (проверьте это, оценив число умножений, необходимых для вычисления ${\mathcal{P}}^T{X}^{T}X\mathcal{P}$).

2. Время для реализации QUBO-задачи в квантовом “железе”. Здесь потребуется $\mathcal{O}(K^2{d}^2)$, если использовать алгоритм из [DPP19].

3. Время для выполнения квантового отжига. Существуют теоретические оценки времени для получения точного решения, но более практично рассматривать случай, когда можно просто довольствоваться достаточно высокой вероятностью (скажем, 99%) получения оптимального решения. Для современных квантовых компьютеров D-Wave с ограниченным числом кубитов на практике получается, что время отжига и число повторений можно считать константами.

В итоге полная временнАя сложность решения QUBO-задачи на адиабатическом квантовом компьютере $\mathcal{O}(N{K}^2{d}^2)$. Может показаться, что это хуже, чем временнАя сложность классического решения, если считать $K$ переменной. Но величина $K$ определяется только шириной диапазона числовых значений и желаемой точностью представления, $K$ не зависит от основных параметров задачи типа $N$ и $d$. Поэтому можно считать $K$ константой. Тогда число требуемых кубитов $\mathcal{O}(d^2)$, временнАя сложность $\mathcal{O}(N{d}^2)$, это эквивалентно классическому случаю.

SVM

Классический SVM подробно описан в соответствующей лекции. Рассматривается тренировочный набор $X\in {\mathbb{R}}^{N\times d}$ и набор истинных меток $Y\in \{-1,+1{\}}^N$. Нужно решить задачу бинарной классификации, найдя веса $w\in {\mathbb{R}}^d$ и константу $b\in \mathbb{R}$, при которых классификатор $a(x_i)=\text{sign}(w^T{x}_i+b)$ допускает как можно меньше ошибок на обучающей выборке.

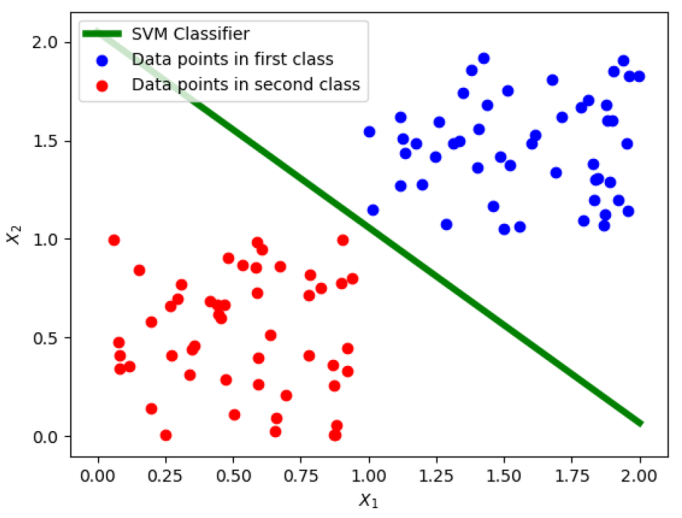
Fig. 95 Иллюстрация к задаче бинарной классификации с помощью SVM.

Двойственная задача (18) в текущих обозначениях принимает вид

(52)$$\begin{array}{r}\{\begin{array}{rl}& \mathcal{L}(\lambda )=\sum _{i=1}^N{\lambda }_i-\frac{1}{2}\sum _{i,j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j⟨x_i,x_j⟩\to \underset{\lambda }{max},\\ & 0\le {\lambda }_i\le C\mathrm{\forall }i\in \{1,2,\dots ,N\},\\ & \sum _{i=1}^N{\lambda }_i{y}_i=0.\end{array}\end{array}$$

QUBO-формулировка

Перепишем (52) как задачу минимизации:

(53)$$\begin{array}{r}\{\begin{array}{rl}& {\mathcal{L}}_{neg}(\lambda )=\frac{1}{2}\sum _{i,j=1}^N{\lambda }_i{\lambda }_j{y}_i{y}_j⟨x_i,x_j⟩-\sum _{i=1}^N{\lambda }_i\to \underset{\lambda }{min},\\ & 0\le {\lambda }_i\le C\mathrm{\forall }i\in \{1,2,\dots ,N\},\\ & \sum _{i=1}^N{\lambda }_i{y}_i=0.\end{array}\end{array}$$

Тренировочные объекты $x_i$, соответствующие ${\lambda }_i=0$, называются периферийными, от них решение

$$w=\sum _{i=1}^N{\lambda }_i{y}_i{x}_i$$

не зависит. Объекты, соответствующие ${\lambda }_i>0$, называются опорными.

Задача минимизации переписывается в виде

(54)$$\begin{array}{r}\{\begin{array}{rl}& {\mathcal{L}}_{neg}(\lambda )=\frac{1}{2}{\lambda }^T(X{X}^T\odot Y{Y}^T)\lambda -{\lambda }^T{1}_N\to \underset{\lambda }{min},\\ & 0_N\le \lambda \le C_N,\\ & {\lambda }^{T}Y=0,\end{array}\end{array}$$

где $1_N$ – вектор, состоящий из $N$ единиц (аналогичный смысл имеют $0_N$ и $C_N$), $\lambda \in {\mathbb{R}}^N$.

Как в задаче линейной регрессии, будем представлять каждую ${\lambda }_i\in \mathbb{R}$ бинарным вектором ${\tilde{\lambda }}_i\in \{0,1{\}}^K$. Поскольку ${\lambda }_i\ge 0$, в precision vector $P$ нужно включить только положительные значения:

$$P={[2^{-m},2^{-m+1},\dots ,2^{l-1},2^l]}^T$$

Вектор $P$ содержит $m+1+l=K$ элементов (здесь $K$ никак не связано с $K$ из раздела про линейную регрессию, просто было решено не вводить новое обозначение для длины нового вектора $P$). При подходящем выборе $m$ и $l$ достаточно точно выполняется равенство

(55)$${\lambda }_i\approx \sum _{k=1}^K{p}_k{\tilde{\lambda }}_{ik}\mathrm{\forall }i\in \{1,2,\dots ,N\}$$

Выполняем конкатенацию всех ${\tilde{\lambda }}_{ik}$ по вертикали

$$\tilde{\lambda }=[\underset{\text{предст. }{\lambda }_1}{\underbrace{{\tilde{\lambda }}_{11}\dots {\tilde{\lambda }}_{1K}}}\underset{\text{предст. }{\lambda }_2}{\underbrace{{\tilde{\lambda }}_{21}\dots {\tilde{\lambda }}_{2K}}}\dots \underset{\text{предст. }{\lambda }_N}{\underbrace{{\tilde{\lambda }}_{N1}\dots {\tilde{\lambda }}_{NK}}}{]}^T$$

и вводим матрицу $\mathcal{P}$ (precision matrix)

$$\mathcal{P}=I_N\otimes P^T$$

таким образом, что (приближенно)

$$\lambda =\mathcal{P}\tilde{\lambda }$$

Подставляя из этого выражения $\lambda$ в (54), получаем:

(56)$$\begin{array}{r}\{\begin{array}{rl}& {\mathcal{L}}_{neg}(\tilde{\lambda })=\frac{1}{2}{\tilde{\lambda }}^T{\mathcal{P}}^T(X{X}^T\odot Y{Y}^T)\mathcal{P}\tilde{\lambda }-{\tilde{\lambda }}^T{\mathcal{P}}^T{1}_N\to \underset{\tilde{\lambda }\in \{0,1{\}}^{NK}}{min}\\ & {\left(\mathcal{P}\tilde{\lambda }\right)}^{T}Y=0\end{array}\end{array}$$

Остается избавиться от ограничения в виде равенства в (56). Как обычно делается в таких случаях, вместо ограничения вводим соответствующий штраф за его нарушение:

$$Penalt{y}^{(hp)}=\frac{\gamma }{2}{\left({\left(\mathcal{P}\tilde{\lambda }\right)}^{T}Y\right)}^2=\frac{\gamma }{2}{\left(\left({\tilde{\lambda }}^T{\mathcal{P}}^T\right)Y\right)}^2=\frac{\gamma }{2}{\tilde{\lambda }}^T{\mathcal{P}}^T\left(Y{Y}^T\right)\mathcal{P}\tilde{\lambda },$$

где $\gamma$ – достаточно большая константа, hp означает hyperplane (гиперплоскость).

Добавляем $Penalt{y}^{(hp)}$ к ${\mathcal{L}}_{neg}(\tilde{\lambda })$ и получаем итоговую QUBO-формулировку:

(57)$$\frac{1}{2}{\tilde{\lambda }}^T{\mathcal{P}}^T(X{X}^T\odot Y{Y}^T+\gamma Y{Y}^T)\mathcal{P}\tilde{\lambda }-{\tilde{\lambda }}^T{\mathcal{P}}^T{1}_N\to \underset{\tilde{\lambda }\in \{0,1{\}}^{NK}}{min}$$

Оценка вычислительной сложности

Задача (54) содержит $\mathcal{O}(Nd)$ значений в данных и $\mathcal{O}(N)$ параметров ($\lambda$). QUBO-формулировка (57) содержит то же количество данных, а число параметров в $K$ раз больше, т.е. $\mathcal{O}(KN)$. Значит, потребуется $\mathcal{O}(N^2{K}^2)$ кубитов.

ВременнАя сложность классического SVM в типичных реализациях (например, LIBSVM) равна $\mathcal{O}(N^3)$. Для оценки временнОй сложности QUBO рассматриваем три составляющие (как в задаче линейной регрессии):

1. Затраты времени для конвертации в QUBO-формулировку. Из (53) и (55) следует, что оценка времени $\mathcal{O}(N^2{K}^2)$.

2. Для реализации QUBO-задачи в квантовом “железе” потребуется $\mathcal{O}(N^2{K}^2)$.

3. Время для выполнения квантового отжига и число повторений можно считать константами (см. комментарии к тому же пункту в обсуждении линейной регрессии).

В итоге временнАя сложность $\mathcal{O}(N^2{K}^2)$. $K$ можно считать константой, т.к. она зависит только от диапазона и желаемой точности представления $\lambda$ и не зависит от параметров самой задачи классификации. Тогда получается временная сложность $\mathcal{O}(N^2)$, что гораздо лучше оценки $\mathcal{O}(N^3)$ в классическом случае.

Сбалансированная кластеризация методом k-средних

Кластеризация методом k-средних – ML-задача обучения без учителя (unsupervised). Требуется распределить тренировочные объекты по $k$ кластерам так, чтобы суммарное отклонение тренировочных объектов, принадлежащих кластерам, от центроидов (центров масс) соответствующих кластеров было минимальным. Сбалансированная кластеризация методом k-средних – частный случай, в котором каждый кластер содержит примерно одно и то же количество объектов $N/k$, как показано на Fig. 96.

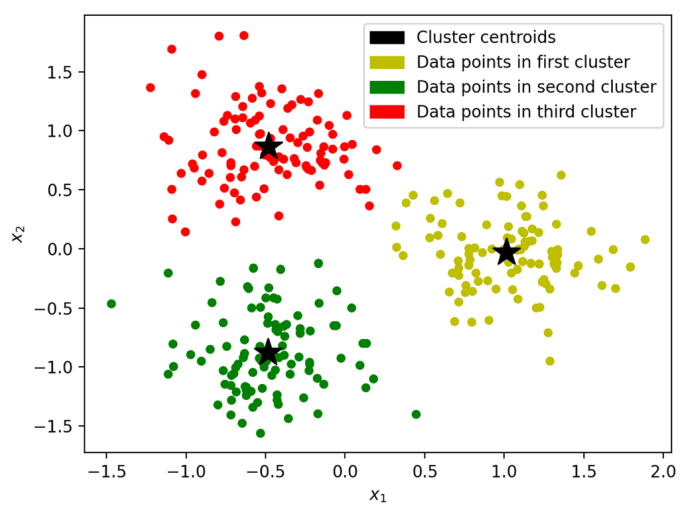
Fig. 96 Иллюстрация к задаче сбалансированной кластеризации методом k-средних.

Нужно распределить $N$ объектов из тренировочного набора $X\in {\mathbb{R}}^{N\times d}$ по $k$ кластерам $\mathrm{\Phi }=\{{\varphi }_1,\dots ,{\varphi }_k\}$. Пусть ${\mu }_i$ – центроид кластера ${\varphi }_i$. В общем случае задача кластеризации методом k-средних формулируется так:

(58)$$\sum _{i=1}^k\frac{1}{2|{\varphi }_i|}\sum _{x,y\in {\varphi }_i}||x-y|{|}^2\to \underset{\mathrm{\Phi }}{min}$$

Если размеры $|{\varphi }_i|$ всех кластеров одинаковые, то формулировка переписывается так:

(59)$$\sum _{i=1}^k\sum _{x,y\in {\varphi }_i}||x-y|{|}^2\to \underset{\mathrm{\Phi }}{min}$$

В прикладных задачах кластеризации размеры кластеров только приближенно равны друг другу, поэтому решение задачи (59) не является точным решением задачи (58). Для решения задачи кластеризации методом k-средних можно использовать, например, алгоритм Ллойда. Существует модификация алгоритма Ллойда для случая сбалансированной кластеризации.

QUBO-формулировка

Вводим матрицу $D\in {\mathbb{R}}^{N\times N}$, элементы которой равны квадратам попарных расстояний между тренировочными объектами:

$$d_{ij}=||x_i-x_j|{|}^2$$

Также вводим бинарную матрицу $\tilde{W}\in \{0,1{\}}^{N\times k}$, каждый элемент которой ${\tilde{w}}_{ij}=1$ в том и только в том случае, когда объект $x_i$ принадлежит кластеру ${\varphi }_j$. Очевидно, есть два ограничения на $\tilde{W}$:

1. Поскольку мы предполагаем, что все кластеры содержат примерно одно и тоже количество объектов, каждый столбец $\tilde{W}$ должен содержать примерно $N/k$ единиц.

2. Каждый объект принадлежит ровно одному кластеру, поэтому каждая строка $\tilde{W}$ должна содержать ровно одну единицу.

Для получения QUBO-формулировки задачи нам потребуется избавиться от этих ограничений. Для этого, как обычно, введем в минимизируемую квадратичную форму штрафы за нарушение ограничений. Вернемся к этому через пару абзацев.

Используя $D$ и $\tilde{W}$, мы можем переписать внутреннюю сумму в (59) в виде

$$\sum _{x,y\in {\varphi }_i}||x-y|{|}^2={{\tilde{w}}_j^{{}^{\prime }}}^{T}D{\tilde{w}}_j^{{}^{\prime }},$$

где ${\tilde{w}}_j^{{}^{\prime }}$ – столбец номер j в $\tilde{W}$. Чтобы переписать в бинарных переменных полную (двойную) сумму в (59), составим вектор-столбец из всех $Nk$ элементов матрицы $\tilde{W}$:

$$\tilde{w}=[{\tilde{w}}_{11}\dots {\tilde{w}}_{N1}{\tilde{w}}_{12}\dots {\tilde{w}}_{N2}\dots {\tilde{w}}_{1k}\dots {\tilde{w}}_{Nk}{]}^T$$

При условии, что ограничения на $\tilde{w}$ выполнены, запишем задачу (59) в эквивалентном виде

(60)$${\tilde{w}}^T(I_k\otimes D)\tilde{w}\to \underset{\tilde{w}}{min}$$

Теперь разбираемся с ограничениями на $\tilde{w}$.

Во-первых, каждый столбец $\tilde{W}$ должен содержать примерно $N/k$ единиц. Введем штраф, непосредственно отражающий это требование:

$$Penalt{y}_j^{(col)}=\alpha {({{\tilde{w}}_j^{{}^{\prime }}}^T{\tilde{w}}_j^{{}^{\prime }}-\frac{N}{k})}^2,$$

где $\alpha$ – достаточно большая константа. Раскрыв скобки в предыдущем выражении, можно убедиться, что

$$Penalt{y}_j^{(col)}={{\tilde{w}}_j^{{}^{\prime }}}^T\alpha \underset{\text{обозначим как }F}{\underbrace{(1_N-\frac{2N}{k}{I}_N)}}{\tilde{w}}_j^{{}^{\prime }}+\text{const}$$

Сумма всех штрафов для столбцов равна

$$Penalt{y}^{(col)}=\sum _{j}Penalt{y}_j^{(col)}={\tilde{w}}^T(I_k\otimes \alpha F)\tilde{w}$$

Во-вторых, каждая строка $\tilde{W}$ должна содержать ровно одну единицу. Соответствующий штраф

$$Penalt{y}_i^{(row)}=\beta {({\tilde{w}}_i^T{\tilde{w}}_i-1)}^2,$$

где $\beta$ – достаточно большая константа. Раскрыв скобки в предыдущем выражении, получаем

$$Penalt{y}_i^{(row)}={\tilde{w}}_i^T\beta \underset{\text{обозначим как }G}{\underbrace{(1_k-2I_k)}}{\tilde{w}}_i+\text{const}$$

Чтобы найти сумму $Penalt{y}^{(row)}=\sum _{i}Penalt{y}_i^{(row)}$, преобразуем бинарный вектор $\tilde{w}$ в другой бинарный вектор $\tilde{v}$, получающийся из $\tilde{w}$ определенной перестановкой элементов:

$$\tilde{v}=[{\tilde{w}}_{11}\dots {\tilde{w}}_{1k}{\tilde{w}}_{21}\dots {\tilde{w}}_{2k}\dots {\tilde{w}}_{N1}\dots {\tilde{w}}_{Nk}{]}^T$$

Переход от $\tilde{w}$ к $\tilde{v}$ можно представить как линейное преобразование

$$\tilde{v}=Q\tilde{w}$$

с некоторой матрицей $Q\in \{0,1{\}}^{Nk\times Nk}$ (матрица $Q$ в свою очередь получается из единичной матрицы $I_{Nk}$ определенной перестановкой элементов).

Сумма штрафов для строк равна

$$Penalt{y}^{(row)}=\sum _{i}Penalt{y}_i^{(row)}={\tilde{v}}^T(I_N\otimes \beta G)\tilde{v}={\tilde{w}}^T{Q}^T(I_N\otimes \beta G)Q\tilde{w}$$

Соберем вместе квадратичную форму (60) (записанную без учета ограничений) и штрафы $Penalt{y}^{(col)}$, $Penalt{y}^{(row)}$ в одно финальное выражение, которое и является QUBO-формулировкой задачи о сбалансированной кластеризации методом k-средних:

(61)$${\tilde{w}}^T(I_k\otimes (D+\alpha F)+Q^T(I_N\otimes \beta G)Q)\tilde{w}\to \underset{\tilde{w}}{min}$$

Оценка вычислительной сложности

Задача (59) содержит $\mathcal{O}(Nd)$ значений в данных и $\mathcal{O}(N)$ переменных. В QUBO-формулировке вводим по $k$ бинарных переменных для каждой исходной. Получается $\mathcal{O}(Nk)$ переменных, а значит, требуется $\mathcal{O}(N^2{k}^2)$ кубитов.

Известно, что классический алгоритм сбалансированной кластеризации методом k-средних сходится за время $\mathcal{O}(N^{3.5}{k}^{3.5})$ в худшем случае (см. ссылки в статье [DAPN21]). Для оценки временнОй сложности QUBO рассматриваем три составляющие:

1. Затраты времени для конвертации в QUBO-формулировку. В выражении (61) по вычислительной сложности доминирует слагаемое, содержащее $I_k\otimes D$. Соответствующая вычислительная сложность $\mathcal{O}(N^{2}kd)$.

2. Для реализации QUBO-задачи в квантовом “железе” потребуется $\mathcal{O}(N^2{k}^2)$.

3. Время для выполнения квантового отжига и число повторений можно считать константами (см. комментарии к тому же пункту в обсуждении линейной регрессии).

В итоге получаем полную вычислительную сложность $\mathcal{O}(N^{2}k(d+k))$. Это лучше, чем результат классического алгоритма в худшем случае. Но количество итераций в классическом алгоритме сильно зависит от “удачности” начального приближения для центроидов кластеров. Классический алгоритм может оказаться и быстрее квантового.

Заключение

В этой лекции были рассмотрены три важные задачи машинного обучения, которые можно переформулировать в виде QUBO (Quadratic Unconstrained Binary Optimization) для решения на квантовом аннилере путем сведения к задаче нахождения основного состояния квантовой системы. Общий подход заключается в том, что минимизируемый в классической формулировке функционал переписывается в виде квадратичной формы относительно бинарных переменных, а вместо условий-ограничений в финальную квадратичную форму QUBO-задачи вводятся штрафы за нарушение этих ограничений. Есть надежда на то, что при некотором количестве кубитов квантовые алгоритмы будут иметь преимущество перед классическими по времени выполнения.