Quantum Approximate Optimization Algorithm
Contents
Quantum Approximate Optimization Algorithm#
Автор(ы):
Введение#
В лекции рассматривается еще один алгоритм для приближенного решения \(NP\)-задач комбинаторный оптимизации, который называется Qauntum Approximate Optimization Algorithm (далее QAOA) [FGG14].
Квантовый отжиг (повторение)#
В прошлых лекция активно рассказывалось о квантовых аннилерах (отжигателях, англ. annealers) – аналоговых устройствах, реализующих поиск основного состояния системы. Выпишем еще раз гамильтониан, который там используется:
В процессе квантового отжига плавно меняются параметры \(A\) и \(B\):
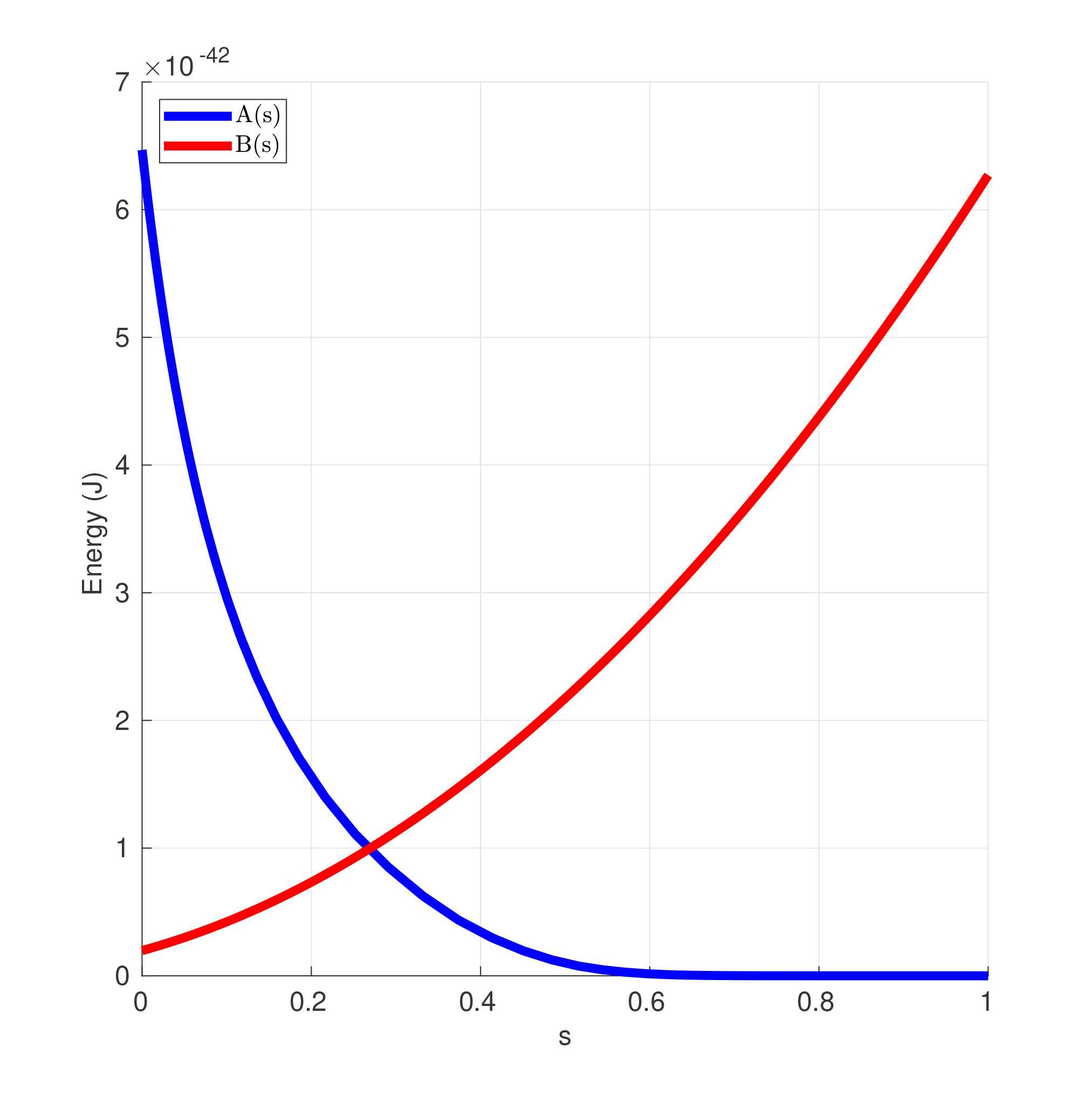
Fig. 115 Пример расписания отжига: функций \(A(t)\), \(B(t)\).#
В той же лекции о D-Wave указывалась главная проблема – риск перехода системы из основного состояния в возбужденное при недостаточно медленном изменении параметров \(A\) и \(B\):
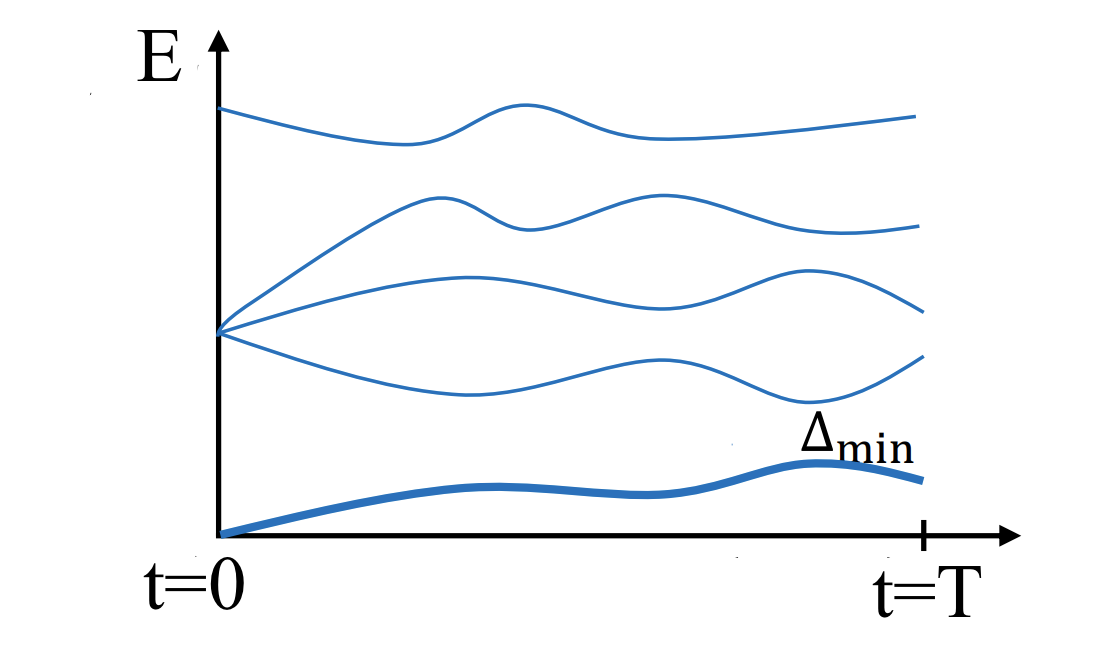
Fig. 116 Типичная зависимость от времени энергетических уровней гамильтонианов, используемых в квантовом отжиге#
Таким образом, большой проблемой для нас является выбор правильного “расписания” отжига, то есть зависимостей \(A(t)\) и \(B(t)\).
От железа к симуляции#
У отжига “в железе” есть существенная проблема – трудно правильным образом подбирать расписание отжига. Но есть и другая идея! Изначально квантовые компьютеры создавались для симуляции квантовой динамики. Воспользуемся техникой симуляции, которая называется trotterization.
Trotterization и симуляция аннилера#
В данном случае наша цель – получить выражение для финального состояния \(\ket{\Psi}\), которое будет отвечать решению квантового отжигателя. Финальное состояние есть решение уравнения Шредингера:
где \(\mathcal{H}_{initial}\) – это tunneling или начальный гамильтониан, а \(\mathcal{H}_{cost}\) – это так называемый problem или cost гамильтониан, который отвечает задаче. Подробно эти темы обсуждались в лекции о D-Wave. Для тех, кто сейчас ничего не понял, рекомендуется также вернуться к лекции о переходе от комбинаторных задач к гамильтонианам, чтобы понять, как получается cost гамильтониан.
Note
Уравнение Шредингера практически не решается численно для сколько-нибудь больших задач, поэтому мы примем как факт то, что точно посчитать квантовую динамику аннилера у нас не выйдет, тем более не выйдет как-то пытаться оптимизировать
Для решения проблемы “нерешаемости” уравнения Шредингера перейдем от непрерывного времени \(t\) и зависимостей \(A(t)\) и \(B(t)\) к \(N\) дискретных моментов времени \(t_1, t_2, ..., t_n\). Тогда можно заменить расписание отжига в виде непрерывных коэффициентов на набор дискретных коэффициентов, каждый из которых отвечает своему моменту времени:
Финальное состояние записывается так:
Оптимизация расписания#
Теперь задача оптимизации расписания по своей сути сведена к следующей:
А это уже хорошо знакомая задача оптимизации результата измерения состояния, заданного при помощи некоторой VQC, которая параметризирована набором действительных чисел \(\gamma_1, ..., \gamma_N, \beta_1, ..., \beta_N\). И эта задача решается хорошо уже знакомыми градиентными методами.
Пример задачи оптимизации#
Рассмотрим задачу оптимизации \(n\)-разрядного набора данных, для которого нужно найти некоторый минимум (или максимум). Алгоритм задается двумя гамильтонианами \(H_{p}\) и \(H_{M}\), а также \(2p\) параметрами: \(\gamma_{1}, ..., \gamma_{p}\) и \(\beta_{1}, ..., \beta_{p}\).
QAOA использует унитарный оператор \(U(\beta,\gamma)\), принимающий на вход вещественные параметры \(\beta\), \(\gamma\), и описывается уже знакомым квантовым состоянием \(\ket{\Psi}\). Цель поиска – найти те самые оптимальные \(\beta_{\text{opt}}\) и \(\gamma_{\text{opt}}\).
Оператор \(U\) состоит из двух частей:
оператор, меняющий фазу \(U_{\text{phase}}\)
\[ U_{\text{phase}}(\gamma) = e^{ -i {\gamma} H_{\text{phase}} } \]оператор, смешивающий кубиты \(U_{\text{mixer}}\)
\[ U_{\text{mixer}}(\beta) = e^{ -i {\beta} H_{\text{mixer}} } \]
Оператор \(U_{\text{phase}}\) совершает вращение относительно осей \(Z\) или \(Y\) с помощью соответствующих матриц Паули
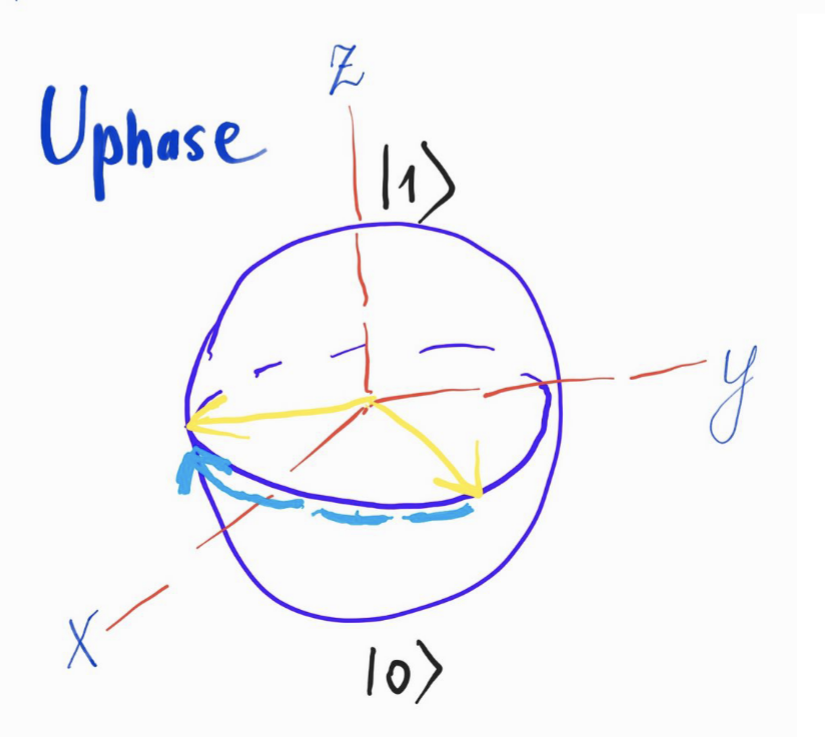
Fig. 117 Оператор \(U_{\text{phase}}\)#
\(U_{\text{mixed}}\) в классическом случае использует матрицу \(XNOT\).
Операторы применяются к начальному состоянию \(\ket{\Psi_{0}}\) (путем поочередного применения гамильтонианов \(H_{p}\) и \(H_{M}\)) последовательно \(р\) раз (или, иначе говоря, используются \(p\) слоев), где продолжительность \(j\)-й итерации определяется параметрами \(\gamma_{j}\) и \(\beta_{j}\) соответственно
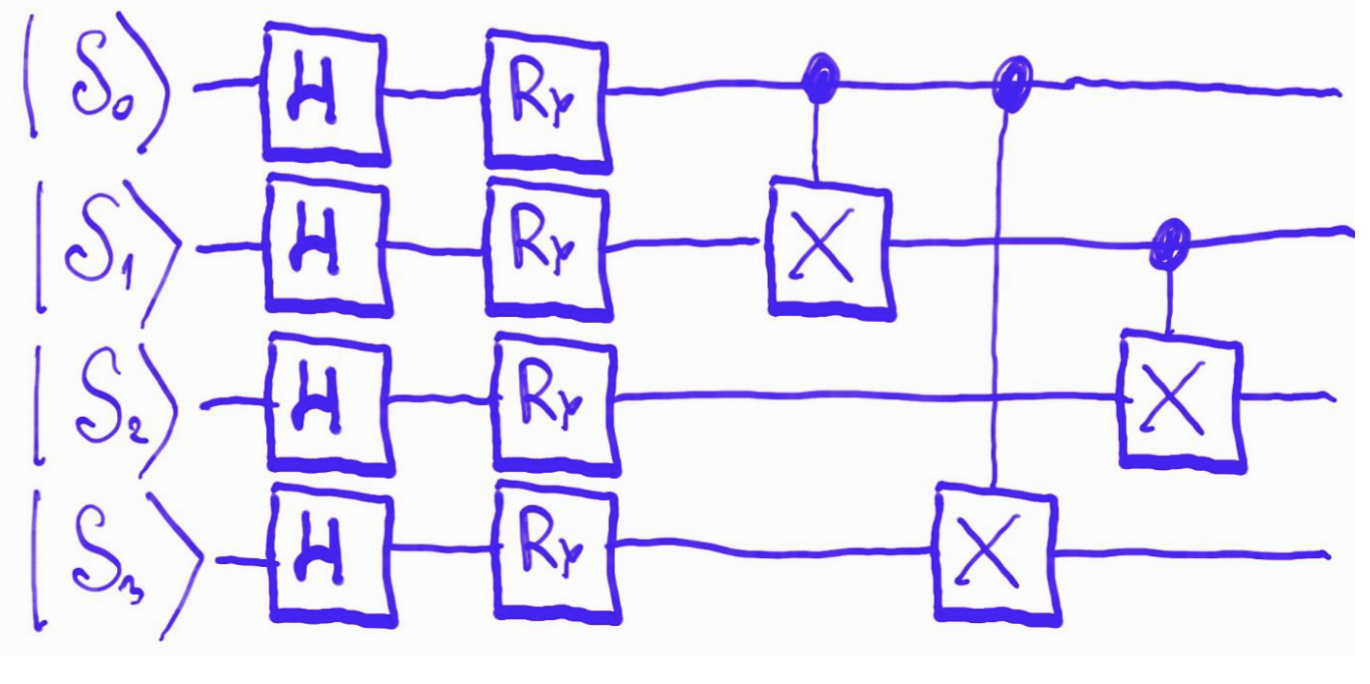
Общая схема для \(n\) кубитов выглядит следующим образом
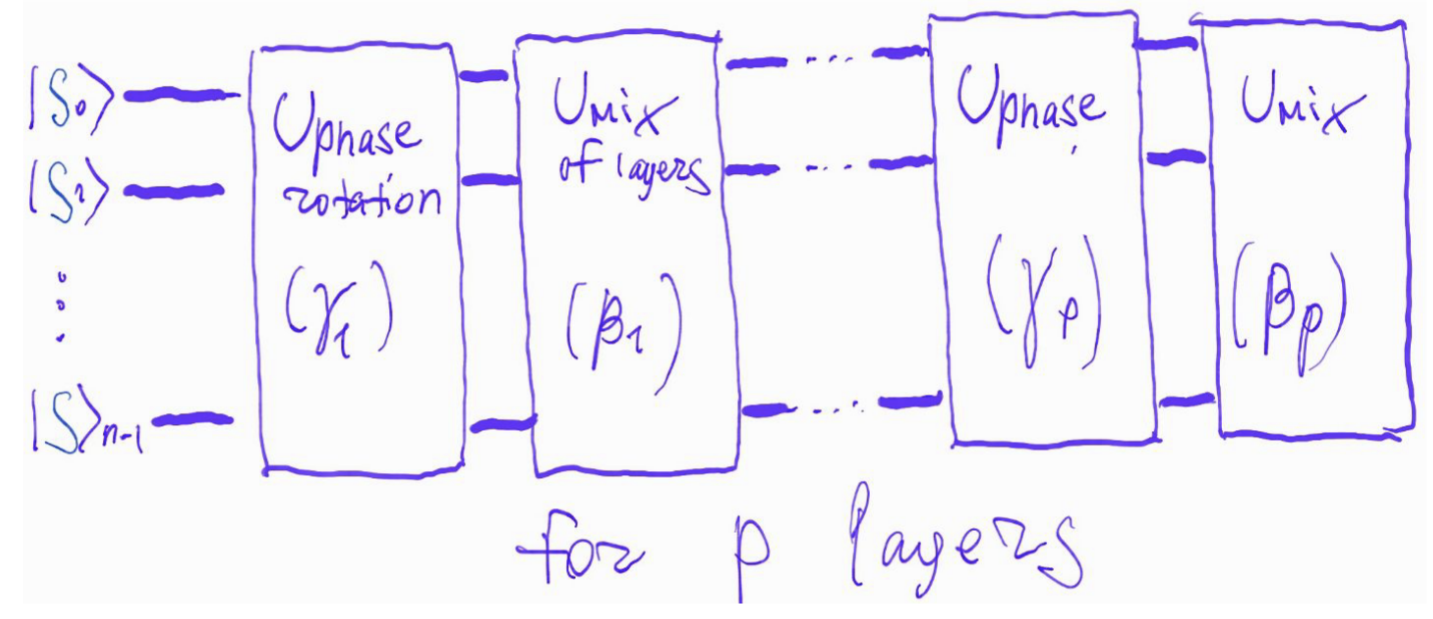
Fig. 118 Общая схема для \(n\) кубитов#
Итак, алгоритм состоит из следующих основных этапов:
приготовление начального состояния \(\ket{\Psi_{0}}\) из \(n\) кубитов. Начальное состояние выбирается как равное состояние суперпозиции всех возможных решений
\[ \ket{\Psi_{0}} = \frac{1}{\sqrt{2^n}} \sum_{x} \ket{x} \]последующее применение к каждому кубиту матриц Адамара для осуществления суперпозиции всевозможных состояний

применяем оператор вращения фазы
\[ U_{\text{phase}} = \sum_{i \neq j}^{n-1} e^{-i \gamma Z_i Z_j} \]например, вот так
\[ H_p = (I_0 \otimes Z_1 \otimes I_2 \otimes Z_3) \]
Напоминаем, как выглядит данный оператор в матричном виде: \(Z = \begin{bmatrix} 1 & 0 \\ 0 & 1\end{bmatrix}\).
применяем смешивающий оператор
\[ U_{\text{mixer}} = \sum_{i=0}^{n-1} e^{-i \beta X_i} \]к примеру, так
\[ U_{\text{mixer}} = (I \otimes I \otimes X \otimes Z) \]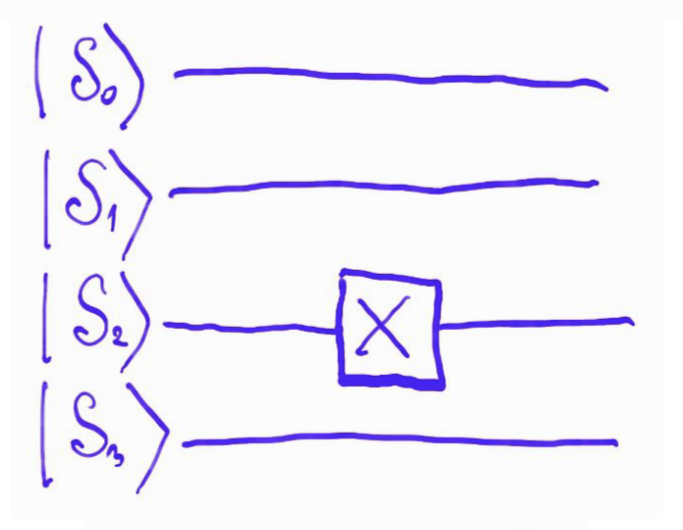 \[\begin{split} X = \begin{bmatrix} 0 & 1 \\ 1 & 0\end{bmatrix} \end{split}\]
\[\begin{split} X = \begin{bmatrix} 0 & 1 \\ 1 & 0\end{bmatrix} \end{split}\]
В данном алгоритме используется адиабатический метод эволюции состояния [FGGS00] \(\ket{\Psi_0}\) с переменным гамильтонианом: на каждой итерации параметры \(\beta\) и \(\gamma\) понемногу изменяются.
Далее производится измерение финального состояния в \(Z\)-базисе и вычисление \(\bra{\Psi(\beta,\gamma)}H_{phase}\ket{\Psi(\beta,\gamma)}\). Найденный минимум будет соответствовать оптимальным \(\beta\) и \(\gamma\).
Описанные выше шаги могут быть полностью повторены с обновлёнными наборами временных параметров в рамках классического цикла оптимизации (такого как градиентный спуск или другие подходы), используемого для оптимизации параметров алгоритма.
Возвращается лучшее решение, найденное за всё время поиска.
Quantum Alternating Operator Ansatz#
Применение “анзаца” в алгоритме квантовой приближенной оптимизации заключается в модернизации оператора смешивания \(U_{mixer}\) и предполагает использование \(CNOT\), а не \(X\).
Анзац рассматривает более общие параметризированные унитарные трансформации, а не только соответствующие эволюции фиксированного локального гамильтониана во времени. Он позволяет более эффективно реализовывать операции смешивания, особенно в задачах оптимизации с жесткими ограничениями.
На рисунках ниже представлена абстрактная визуализация “смешивания” и обозначение оператора:
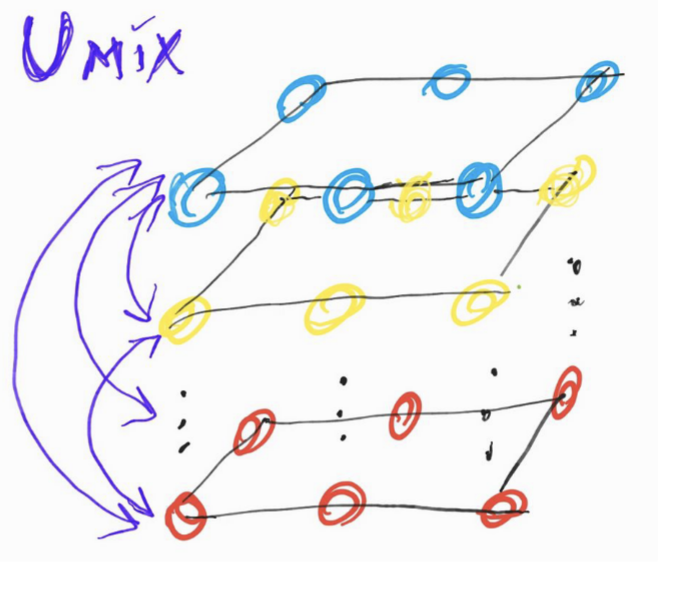
Fig. 119 “Смешивание”#
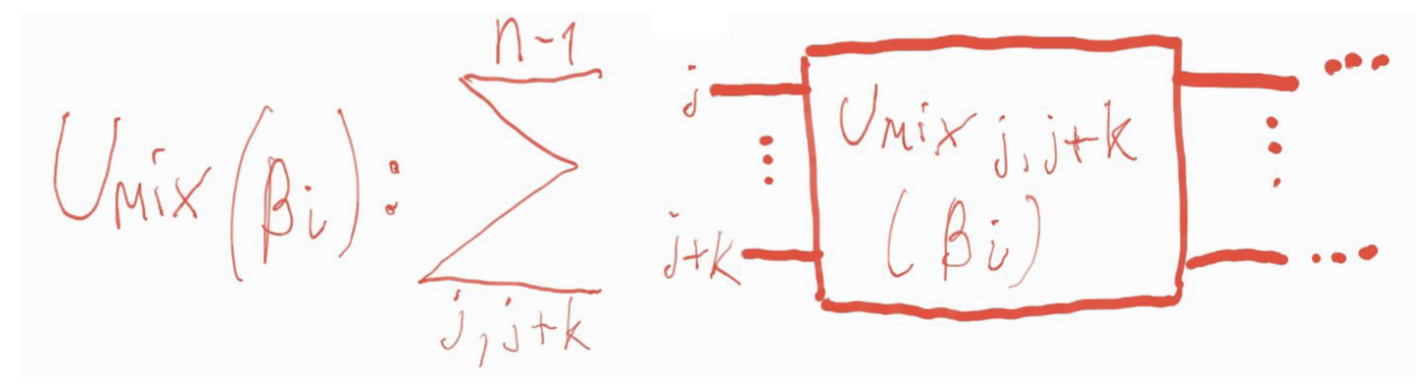
Fig. 120 Обозначение оператора#
Классически семейство анзацев можно поделить на три основных типа:
Hardware Efficient Ansatz (HEA) – запутывающий все кубиты;
Alternating Layered Ansatz (ALT) [FGG14];
Tensor Product Ansatz (TEN) [HPM+19].
На рисунке ниже изображены упрощённые (без учета анзаца и фазовых гейтов) для понимания схемы описанных компоновок – по одному слою каждого типа:
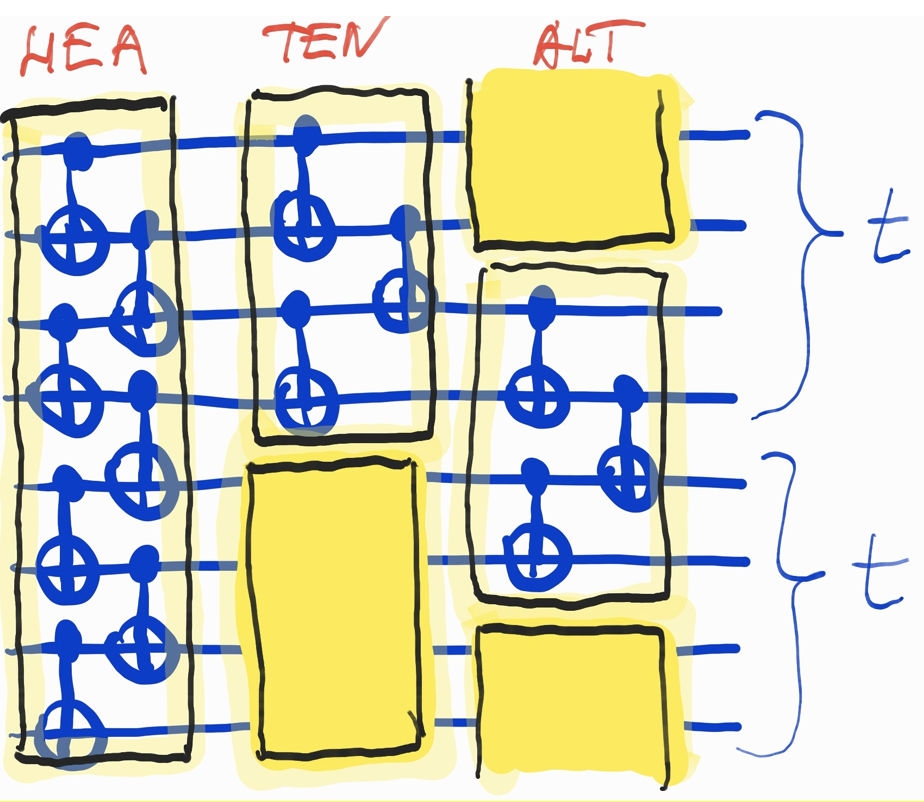
Конечно, к компоновке смешанных гейтов можно подходить сколь угодно творчески, и пример общей схемы, реализующей QAOAz, представлен ниже: