Алгоритм Дойча#

Автор(ы):

Алгоритм Дойча (в английском варианте – Deutsch’s algorithm) – это один из первых алгоритмов, показавших, что квантовый компьютер может решать задачи особым способом, отличающимся как от алгоритмов классического компьютера, так и от интуиции и здравого смысла человека. При этом такое решение может занимать меньшее количество шагов.

Нужно прежде всего сказать, что алгоритм Дойча не имеет практического применения в силу своей предельной простоты, зато является простейшим примером, с помощью которого можно понять, в чем состоит отличие квантовых алгоритмов от классических. Данный алгоритм был предложен в 1985 году, когда квантовых компьютеров еще не было, а практически он был реализован в 1998 году на 2-кубитном квантовом компьютере, работавшем на принципах ядерно-магнитного резонанса.

Дэвид Дойч

Помимо занятий теоретической физикой в Оксфордском университете, Дэвид Дойч – автор книг “Структура реальности” и “Начало бесконечности”, в которых он популярно излагает идеи квантовых вычислений с точки зрения многомировой интерпретеции (сторонником которой является) и философствует о будущем науки и человечества. Так что можно сказать, что работа алгоритма, согласно замыслу создателя, производится в параллельных вселенных. Так это или нет, пока проверить невозможно, но вычисления работают, и это главное.

Итак, в чем состоит задача, которую решает алгоритм? Представьте, что у вас есть функция, которая представляет собой “черный ящик”, принимающий на вход число из множества \(\{0, 1\}\). Функция неким образом обрабатывает входное значение и возвращает число из этого же множества, то есть либо \(0\), либо \(1\). Нам известно, что эта функция принадлежит либо к классу сбалансированных функций, либо к классу константных функций (которые мы также можем называть несбалансированными). Задача алгоритма – установить, к какому классу принадлежит функция.

Рассмотрим все варианты этих двух классов. Всего их четыре, то есть по две функции в каждом классе. Начнем с несбалансированных:

  • \(f_1(x) = 0\)

Это функция, всегда возвращающая \(0\), независимо от входного значения. Для нее справедливы выражения:

\[ f_1(0) = 0 \]
\[ f_1(1) = 0 \]

  • \(f_2(x) = 1\)

Такая функция всегда возвращает \(1\), то есть верно следующее:

\[ f_2(0) = 1 \]
\[ f_2(1) = 1 \]

Ну а теперь посмотрим на сбалансированные функции. Для них характерно то, что они могут возвращать как \(0\), так и \(1\). В этом и заключается “баланс”.

  • \(f_3(x) = x\)

Это тождественная функция, которая ничего не делает с входным значением. Для нее справедливо следующее:

\[ f_3(0) = 0 \]
\[ f_3(1) = 1 \]

  • \(f_4(x) = \overline{x}\)

А вот эта функция инвертирует входное значение, то есть возвращает не то число, которое было подано на вход, а другое:

\[ f_4(0) = 1 \]
\[ f_4(1) = 0 \]

Классический компьютер справляется с задачей за два шага. Например, нам дана некоторая функция-“черный ящик”, и мы должны установить, сбалансирована ли она. На первом шаге мы отправляем в функцию входное значение \(0\). Допустим, мы получили на выходе также \(0\). Мы можем сказать, что данная функция – либо \(f_1\) (константная функция, всегда возвращающая \(0\)), либо \(f_3\) (сбалансированная функция, не меняющая входное значение). Для окончательного решения мы должны сделать еще один шаг – отправить в функцию значение \(1\). Если при этом мы получим опять \(0\), то это функция \(f_1\), а если получили на выходе \(1\), то искомая функция – \(f_3\).

Способа, с помощью которого на классическом компьютере можно за одно действие установить, сбалансирована функция или нет, не существует. И здесь свое преимущество показывает квантовый компьютер: он может установить класс функции за одно действие.

Для начала рассмотрим простейшую схему, с помощью которой можно отправлять число на вход и получать ответ от черного ящика:

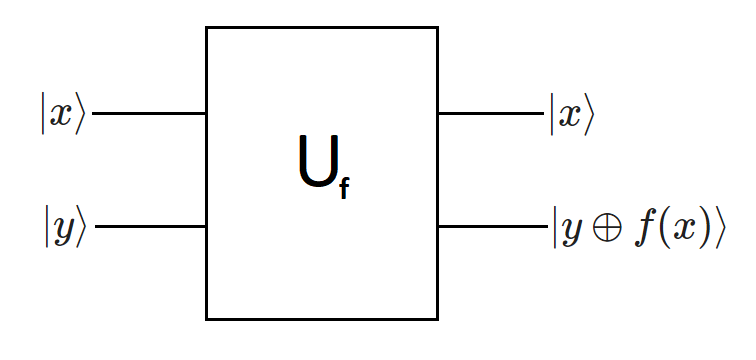
../../../_images/scheme_1.png

Fig. 29 Схема 1#

\(U_f\) на данной схеме – это неизвестная функция (ее также часто называют “оракул”), являющаяся унитарным оператором. Обратите внимание, что в квантовой схеме используются два кубита. Это нужно для того, чтобы информация, с которой работает квантовый компьютер, не стиралась. В квантовом компьютере важно, чтобы все действия с кубитами (кроме операции измерения) были обратимыми, а для этого информация должна сохраняться. В верхнем кубите будет записано входное значение, а в нижнем – выходное значение функции. Таким образом, входное значение не будет перезаписано значением, которое вернет функция.

Но нам важно будет не только сохранить значение \(|x\rangle\), но также и не разрушить \(|y\rangle\). Так как кубит \(y\) очевидно имеет некоторое изначальное значение, мы не можем его просто перезаписать тем числом, которое выдаст функция \(f(x)\). Здесь на помощь приходит операция исключающее ИЛИ - \(XOR\) (также ее можно называть сложением по модулю 2), обозначенная на схеме как \(\oplus\). В процессе работы черный ящик \(U_f\) не только находит значение \(f(x)\), но и применяет исключающее ИЛИ к значениям \(y\) и \(f(x)\).

Операции \(XOR\) соответствует такая таблица истинности:

a

b

a XOR b

0

0

0

0

1

1

1

0

1

1

1

0

Операция \(XOR\) хороша для нас тем, что она не разрушает значение \(|y\rangle\), так как является обратимой. Убедиться в этом можно, проверив тождество:

\[ (a \oplus b) \oplus b = a \]

Схема 1 пока что не дает преимущества по сравнению с классическим компьютером, но мы можем ее немного усовершенствовать:

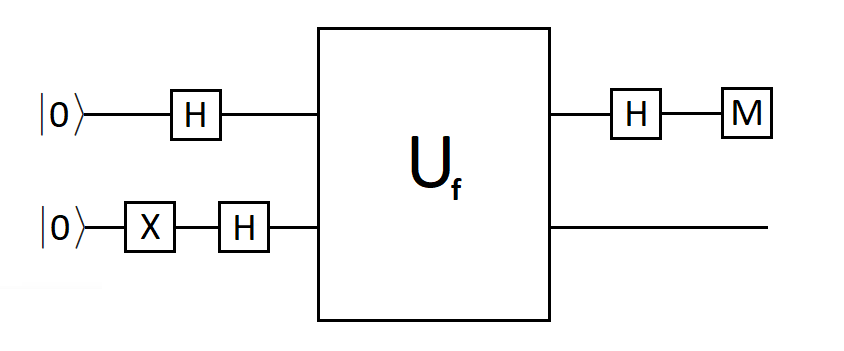
../../../_images/scheme_2.png

Fig. 30 Схема 2#

В новой схеме оба кубита вначале будут находиться в состоянии \(|0\rangle\). Затем мы применим к верхнему кубиту оператор Адамара, а к нижнему – гейт \(X\), а затем так же, как и к верхнему, оператор Адамара. Тем самым мы приведем оба кубита в состояние суперпозиции перед тем, как они попадут на вход функции \(U_f\). Верхний кубит будет находиться в такой суперпозиции:

\[ |x\rangle = \frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle, \]

а нижний - в такой:

\[ |y\rangle = \frac{1}{\sqrt{2}}|0\rangle - \frac{1}{\sqrt{2}}|1\rangle. \]

Если рассмотреть это как систему \(|\psi\rangle\), состоящую из двух кубитов, то она будет выглядеть так:

\[ |\psi\rangle = \frac{1}{2}(|0\rangle + |1\rangle)(|0\rangle - |1\rangle) \]

Сразу после \(U_f\) система будет находиться в состоянии:

\[|\psi\rangle = \frac{1}{2}(|0\rangle + |1\rangle)(|0 \oplus f(x)\rangle - |1 \oplus f(x)\rangle) \]

После того, как \(U_f\) отрабатывает, нижний кубит, как это ни странно, уже нас не интересует, так что к нему операции больше не применяются, и его измерение также не производится.

Дело в том, что ответ на вопрос о том, сбалансирована функция \(f(x)\) или нет, будет нами получен из верхнего кубита после того, как на него подействует оператор Адамара и будет произведено измерение. В том случае, если функция сбалансирована, результат измерения верхнего кубита будет равен \(1\), а если несбалансированна – \(0\).

Разберемся подробнее, почему это происходит. Рассмотрим все возможные \(f(x)\), которые могут находиться в черном ящике:

  • \(f(x) = f_1\)

В этом случае \(f(x)\) всегда принимает значение \(0\), и система кубитов будет выглядеть так:

\[ |\psi\rangle = \frac{1}{2}(|0\rangle + |1\rangle)(|0\rangle - |1\rangle) = \frac{1}{2}(|00\rangle - |01\rangle + |10\rangle - |11\rangle) \]

  • \(f(x) = f_2\)

\(f(x)\) будет равно \(1\) независимо от аргумента. Используя таблицу истинности XOR, легко убедиться, что во второй скобке \(|0\rangle\) и \(|1\rangle\) поменяются местами, но если вынести минус за скобку, то мы можем его не учитывать, так общий фазовый множитель (-1 в данном случае) для системы не имеет значения:

\[ |\psi\rangle = \frac{1}{2}(|0\rangle + |1\rangle)(|1\rangle - |0\rangle) = -\frac{1}{2}(|0\rangle + |1\rangle)(|0\rangle - |1\rangle) = -\frac{1}{2}(|00\rangle - |01\rangle + |10\rangle - |11\rangle) \]

Видно, что при применении функций \(f_1\) и \(f_2\), являющихся несбалансированными, мы получаем фактически одно и тоже состояние. Если после этого применить к первому кубиту оператор Адамара, то после измерения мы получим значение \(0\).

Рассмотрим теперь сбалансированные функции \(f_3\) и \(f_4\).

  • \(f(x) = f_3\)

Здесь ситуация сложнее, так как \(f(x)\) будет зависеть от состояния первого кубита. Поэтому мы раскроем скобки, а значения функции подставим позже:

\( |\psi\rangle = \frac{1}{2}(|0\rangle + |1\rangle)(|0 \oplus f(x)\rangle - |1 \oplus f(x)\rangle) = \frac{1}{2}(|0\rangle |0 \oplus f(x)\rangle - |0\rangle |1 \oplus f(x)\rangle + |1\rangle |0 \oplus f(x)\rangle - |1\rangle |1 \oplus f(x)\rangle)=\)

\( =\frac{1}{2}(|0\rangle |0 \oplus 0\rangle - |0\rangle |1 \oplus 0\rangle + |1\rangle |0 \oplus 1\rangle - |1\rangle |1 \oplus 1\rangle) = \frac{1}{2}(|00\rangle - |01\rangle + |11\rangle - |10\rangle) =\)

\( =\frac{1}{2}(|00\rangle - |01\rangle - |10\rangle + |11\rangle) = \frac{1}{2}(|0\rangle - |1\rangle)(|0\rangle - |1\rangle)\)

Видно, что первый кубит поменял свое состояние - теперь он в суперпозиции \(\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\), так что далее к нему можно применить оператор Адамара, после которого он перейдет в состояние \(|1\rangle\).

  • \(f(x) = f_4\)

Здесь будет похожая ситуация:

\( |\psi\rangle = \frac{1}{2}(|0\rangle + |1\rangle)(|0 \oplus f(x)\rangle - |1 \oplus f(x)\rangle) = \frac{1}{2}(|0\rangle |0 \oplus f(x)\rangle - |0\rangle |1 \oplus f(x)\rangle + |1\rangle |0 \oplus f(x)\rangle - |1\rangle |1 \oplus f(x)\rangle)=\)

\( =\frac{1}{2}(|0\rangle |0 \oplus 1\rangle - |0\rangle |1 \oplus 1\rangle + |1\rangle |0 \oplus 0\rangle - |1\rangle |1 \oplus 0\rangle) = \frac{1}{2}(|01\rangle - |00\rangle + |10\rangle - |11\rangle) =\)

\( =-\frac{1}{2}(|00\rangle - |01\rangle + |11\rangle - |10\rangle) =-\frac{1}{2}(|0\rangle - |1\rangle)(|0\rangle - |1\rangle)\)

Получили то же состояние \(|\psi\rangle\), что и для \(f_3\), с точностью до фазового множителя. Соответственно, здесь первый кубит после применения оператора Адамара также будет измерен с результатом \(1\).

Теперь можно получить более компактную формулу, которая подходит для всех четырех функций:

\[ |\psi\rangle = \frac{1}{2}((-1)^{f(0)}|0\rangle + (-1)^{f(1)}|1\rangle)(|0\rangle - |1\rangle) \]

Задание

С помощью квантовых операторов попробуйте создать \(U_f\) для всех четырех \(f(x)\).

Задание рекомендуется сделать до прочтения программистской части по алгоритму Дойча, так как там содержится ответ.

Алгоритм Дойча в коде#

Запрограммируем алгоритм с помощью библиотеки PennyLane. Предполагается, что функция, находящаяся в черном ящике, изначально присутствует, но для учебного примера создадим также и ее, точнее, все ее четыре варианта. Для того, чтобы нам не сразу было известно, какая из этих функций анализируется алгоритмом (иначе будет неинтересно), будем использовать случайный выбор функции.

Импортируем все необходимые библиотеки и модули, а также создадим квантовое устройство-симулятор, рассчитанное на схему из двух кубитов:

import pennylane as qml
from pennylane import numpy as np

dev = qml.device("default.qubit", shots=1, wires=2)

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
  warnings.warn("Setuptools is replacing distutils.")

Теперь создадим функции для черного ящика. Обратите внимание, что здесь уже учтено сложение по модулю \(2\) результата функции с состоянием второго кубита:

def f1():
    pass

def f2():
    qml.PauliX(wires=[1])

def f3():
    qml.CNOT(wires=[0, 1])

def f4():
    qml.PauliX(wires=0)
    qml.CNOT(wires=[0, 1])
    qml.PauliX(wires=0)

Создадим словарь с функциями и их названиями:

black_boxes_dict = {"f1": f1, "f2": f2, "f3": f3, "f4": f4}

А вот таким образом мы будем случайно выбирать название функции для черного ящика:

def random_black_box(black_boxes_dict):
    black_boxes_dict_list_keys = list(black_boxes_dict.keys())
    n = np.random.randint(0, len(black_boxes_dict_list_keys))

    return black_boxes_dict_list_keys[n]

А теперь самое важное – сам алгоритм Дойча:

@qml.qnode(dev, interface=None)
def circuit(black_box_name):
    qml.Hadamard(wires=0)
    qml.PauliX(wires=1)
    qml.Hadamard(wires=1)

    black_boxes_dict[black_box_name]()
    qml.Hadamard(wires=0)

    return qml.sample(qml.PauliZ([0]))

Итак, подготовительные действия завершены, можно приступать к демонстрации работы алгоритма.

Выберем случайным образом функцию:

black_box_name = random_black_box(black_boxes_dict)

А затем запустим алгоритм Дойча и выведем результат его работы. Собственное значение \(1\) оператора \(Z\) будет соответствовать состоянию \(|0\rangle\) (функция несбалансированная), а собственное значение \(-1\) – состоянию \(|1\rangle\) (функция сбалансирована):

result = circuit(black_box_name)
print(result)

1

Проверим, насколько правильно сработал алгоритм. Для этого посмотрим на функцию из черного ящика:

print(black_box_name)

f2

Также посмотрим, как выглядит квантовая схема:

qml.drawer.use_style("default")
fig, ax = qml.draw_mpl(circuit)(black_box_name)
fig.show()
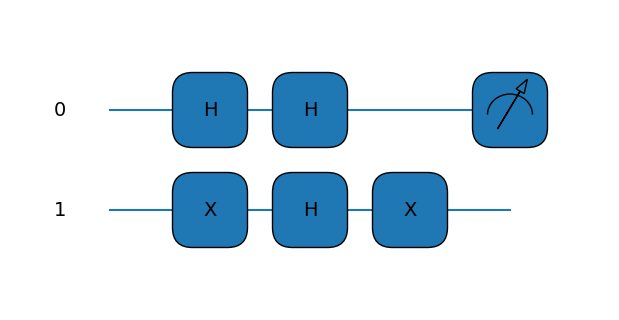
../../../_images/deutschs_algorithm_17_0.png

На примере алгоритма Дойча мы видим, что уже двухкубитная схема дает прирост скорости в два раза. Если же увеличивать количество входных параметров (как в аналогичном алгоритме Дойча-Йожи), то ускорение будет экспоненциальным.

Для специалистов, занимающихся искусственным интеллектом, алгоритм может быть интересен тем, что не просто решает задачу нахождения некоторого значения, действуя как калькулятор, а дает возможность определить скрытую функцию. Это похоже на задачи машинного обучения, когда дата сайентист, производя математические манипуляции с данными, в итоге получает модель (фактически – функцию), описывающую связь признаков с целевой переменной. Таким образом, интерес специалистов ИИ к квантовым вычислениям, вполне понятен, как и перспективы квантовых вычислений в этой области.