Алгоритм Гровера

Автор(ы):

• Ширкин Сергей

Одно из самых востребованных действий в работе с данными – поиск по базе данных. При использовании классического компьютера такой поиск в худшем случае требует \(N\) операций, где \(N\) – количество строк в таблице. В среднем найти нужный элемент можно за \(N/2\) операций.

Фактически, это означает, что если мы не знаем, где расположен нужный элемент в таблице, то придется перебирать все элементы, пока не найдем то, что нужно. Для классических вычислений это нормально, но что, если у нас есть квантовый компьютер?

Если наша база данных работает на основе квантовых вычислений, то мы можем применить алгоритм Гровера, и тогда такой поиск потребует всего порядка \(\sqrt{N}\) действий. Конечно же, такое ускорение не будет экспоненциальным, как при использовании некоторых других квантовых алгоритмов, но оно будет квадратичным, что также довольно неплохо.

Fig. 32 Лов Гровер

Лов Гровер

Индо-американский ученый в сфере Computer Science Лов Кумар Гровер предложил квантовый алгоритм поиска по базе данных в 1996 году. Этот алгоритм считается вторым по значимости для квантовых вычислений после алгоритма Шора. Впервые он был реализован на простейшем квантовом компьютере в 1998 году, а в 2017 году алгоритм Гровера был впервые запущен для трехкубитной базы данных.

Итак, наша задача состоит в том, что мы должны найти идентификационный номер (\(Id\)) записи, которая удовлетворяет определенным условиям. Функция-оракул находит такую запись (для простоты будем сначала считать, что такая запись одна) и помечает соответствующий ей \(Id\). Отметка делается достаточно оригинальным способом: \(Id\) умножается на \(-1\).

Для полной ясности соотнесем количество \(Id\) с числом кубитов в квантовой схеме. Здесь все очень просто: имея \(n\) кубитов, можно закодировать \(N = 2^n\) идентификаторов. К примеру, если в таблице базы данных \(1024\) записей, то закодировать все \(Id\) можно с помощью десяти кубитов.

Для того, чтобы не запутаться в квантовых операциях, рассмотрим пример поменьше: с помощью двух кубитов закодируем четыре идентификационных номера, один из которых будет помечен функцией-оракулом как искомый – он будет домножен на \(-1\). Все эти четыре числа могут существовать в квантовой схеме одновременно, если кубиты приведены в состояние суперпозиции.

Пусть искомый \(Id\) равен \(11\) (будем пользоваться двоичной системой и вести счет с нуля), тогда после работы функции-оракула мы будем иметь \(4\) состояния: \(|00\rangle\), \(|01\rangle\), \(|10\rangle\), \(-|11\rangle\). Проблема в том, что если измерить эту схему, то с равной вероятностью будет обнаружено одно из этих четырех значений, но узнать, какое из них функция-оракул пометила минусом, будет невозможно.

Получается, что одной функции-оракула недостаточно, нужно что-то дополнительное. На помощь приходит алгоритм Гровера. Правда, у него есть такая особенность – он является итерационным, то есть определенные операции (в том числе и применение функции-оракула) нужно повторить несколько раз (порядка \(\sqrt{N}\)). Причем, с количеством итераций нельзя ошибиться, иначе алгоритм даст неправильный ответ.

В идеале после всех итераций квантовую схему можно будет измерить и получить значение \(Id\) искомой записи в таблице базы данных.

Разберем операции, которые включает в себя каждая итерация, но перед этим добавим в схему еще один кубит, который мы будем называть вспомогательным. Он нужен для хранения метки искомого индекса. Звучит не совсем понятно, но ничего сложного в этом нет, все станет ясным после разбора работы функции-оракула. Итак, наша база данных двухкубитная, но сама схема состоит из трех кубитов.

Квантовая схема выглядит так:

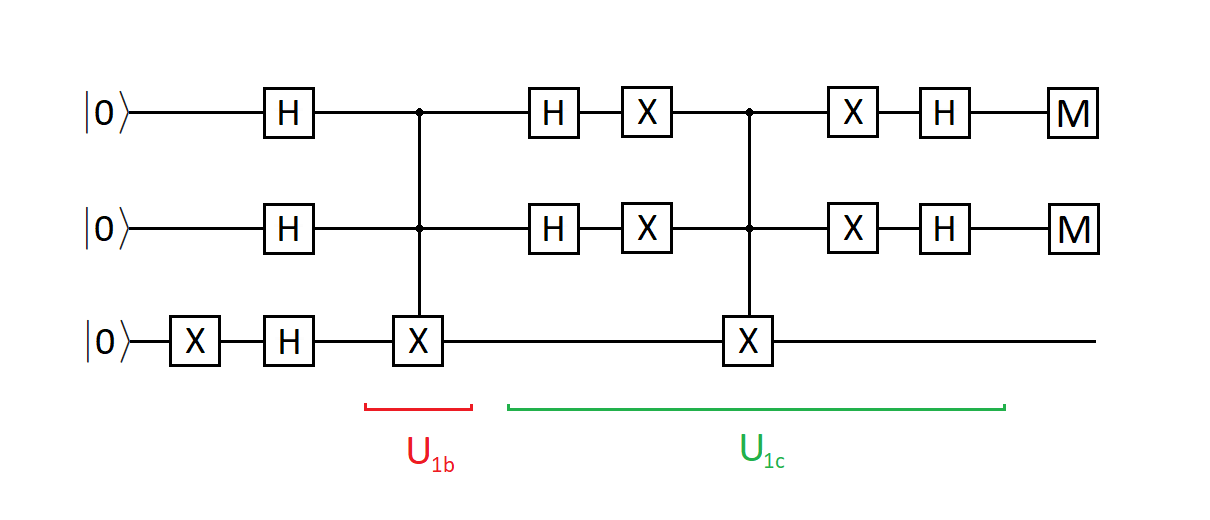
Fig. 33 Алгоритм Гровера для n=2 (искомый индекс 11).

В самом начале, еще до всех итераций, все кубиты (включая вспомогательный) должны быть приведены в состояние суперпозиции с помощью оператора Адамара. Причем начальное состояние всех кубитов должно быть равно \(0\), кроме вспомогательного кубита – до действия оператора Адамара он должен быть приведен в состояние \(1\).

Таким образом, вспомогательный кубит после применения оператора Адамара будет находиться в состоянии \(\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\), тогда как остальные кубиты примут состояние \(\frac{1}{\sqrt{2}}(|0\rangle + |1\rangle)\).

Далее начинаем итерации. Каждая итерация состоит из двух частей. Первая часть – это действие функции-оракула. Это некоторая функция, умеющая эффективно определять, какой индекс соответствует искомому объекту. Эта функция не может сообщить нам этот индекс напрямую, зато она может пометить его минусом.

Для разбора внутренней работы алгоритма нам потребуется задать функцию-оракул вручную и сделать ее достаточно простой, поэтому нужно знать, что в рабочих условиях она будет действовать похоже, но будет устроена, скорее всего, по-другому, так как предназначена для конкретной задачи выбора искомых данных. Мы не будем касаться вопроса конкретной реализации функции-оракула для выбора определенных данных, так как это уже другой вопрос, не влияющий на принцип алгоритма Гровера.

Для того чтобы понять алгоритм Гровера, мы должны будем понять, какие изменения происходят с состояниями кубитов до того момента, когда производится измерение, выдающее искомый индекс.

Мы договорились, что в нашей учебной задаче искомый \(Id\) равен \(11\), так что в результате измерения мы должны получить именно это значение. Смоделируем оракул, который будет помечать этот индекс. В качестве такого оракула подойдет гейт Тоффоли (\(CCNOT\)). При подаче на оба его управляющих входа значений \(1\), он будет применять к управляемому кубиту (это как раз будет вспомогательный кубит) гейт \(X\).

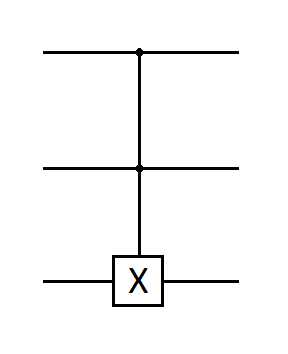
Fig. 34 Гейт Тоффоли.

На состояния верхних кубитов, кодирующих индексы \(00\), \(01\) и \(10\) гейт Тоффоли не будет реагировать, и вспомогательный кубит будет находиться в состоянии \(\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\).

Но при срабатывании гейта на индексе \(11\) к вспомогательному кубиту применится оператор \(X\), так что вспомогательный кубит примет состояние \(\frac{1}{\sqrt{2}}(|1\rangle - |0\rangle)\), или, если это состояние записать по-другому, за скобками появится минус: \(-\frac{1}{\sqrt{2}}(|0\rangle - |1\rangle)\).

Этот минус относится не только к вспомогательному кубиту, но и ко всему состоянию, соответствующему индексу \(11\), так что можно считать, что вспомогательный кубит остался неизменным, и отнести минус к состоянию \(11\) верхних кубитов. Таким образом, индекс \(11\) помечен минусом как искомый. Другими словами, функция-оракул перевела состояние \(|11\rangle |q_{helper}\rangle\) в состояние \(-|11\rangle |q_{helper}\rangle\), где \(|q_{helper}\rangle\) – вспомогательный кубит.

Запишем состояние квантовой схемы после применения оракула (состояние вспомогательного кубита – скобка справа):

\[ |\psi\rangle = \frac{1}{2\sqrt{2}}(|00\rangle + |01\rangle + |10\rangle - |11\rangle)(|0\rangle - |1\rangle) \]

Итак, первая часть первой итерации завершена. Искомый индекс помечен, но если измерить кубиты прямо сейчас, то это ничего не даст – минус не проявит себя при измерении. Да и сам индекс \(11\) будет получен только с вероятностью \(0.25\) – такой же, как и у других индексов.

Для того, чтобы лучше понять дальнейшие действия, представим первую половину работы алгоритма в виде рисунка, показывающего вектор текущего состояния. В качестве единичного вектора горизонтальной оси мы будем использовать все состояния из суперпозиции кроме того, который соответствует искомому индексу, а вертикальным единичным вектором будет искомый вектор.

Вектор \(c\) – состояние системы перед первой итерацией – является линейной комбинацией векторов, соответствующим горизонтальной и вертикальной осям.

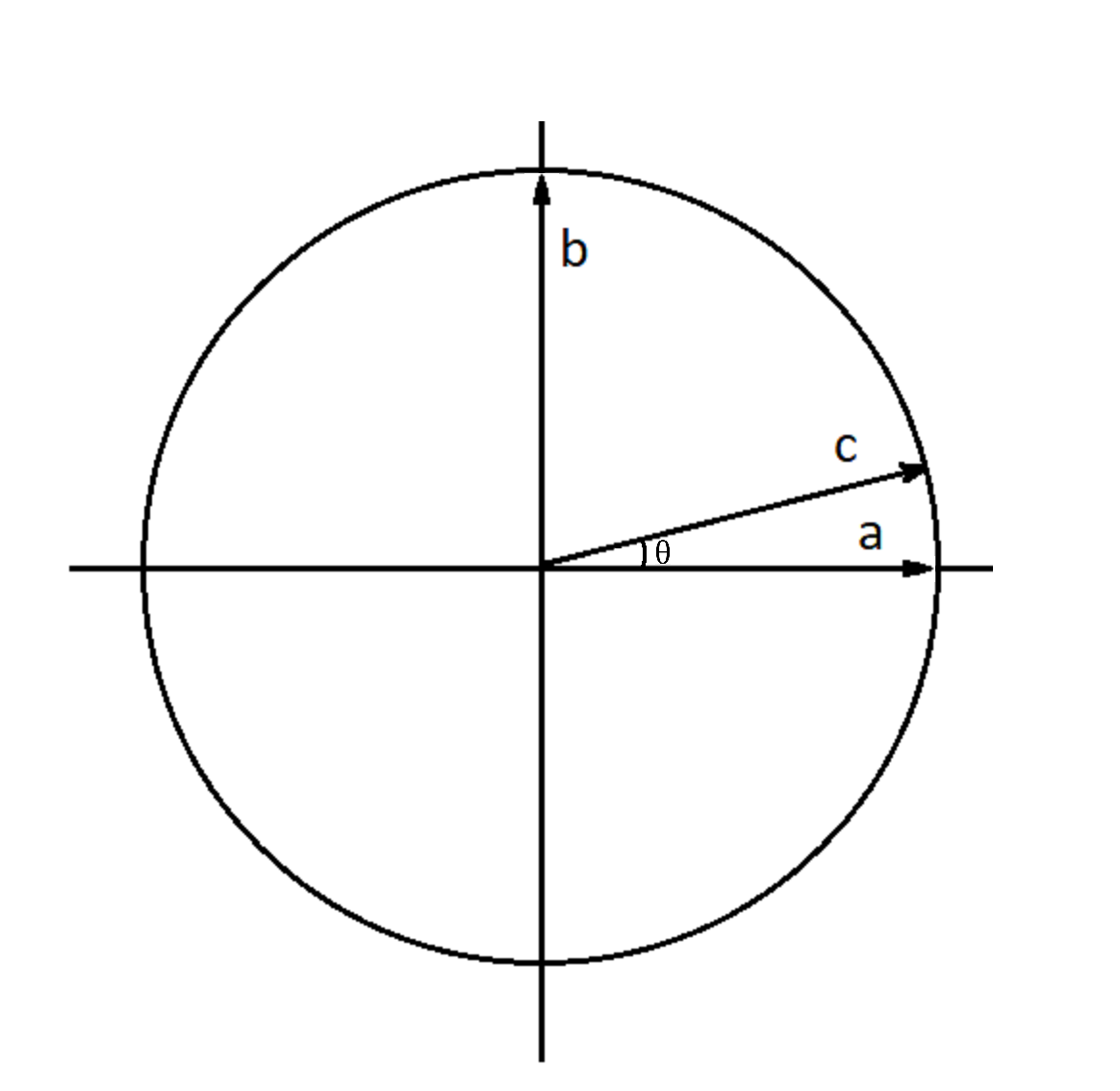
Fig. 35 Состояние системы перед первой итерацией.

Можно выразить вектор \(c\) для нашего случая (системы из двух кубитов с искомым индексом \(11\)), обозначив его координаты за \(x\) и \(y\):

\[ \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) = x \frac{1}{\sqrt{3}}(|00\rangle + |01\rangle + |10\rangle) + y |11\rangle \]

Из данного уравнения находим \(x = \frac{\sqrt{3}}{2}\) и \(y = \frac{1}{2}\).

По этим координатам можно понять, что угол между вектором \(с\) и горизонтальной осью (обозначим его как \(\theta\)) равен \(\frac{\pi}{6}\). Если забежать немного вперед, то можно сказать, что наша цель – добиться, чтобы текущее состояние дошло до \(\frac{\pi}{2}\) (или хотя бы приблизительно), то есть почти или полностью равнялось искомому состоянию, так что после измерения можно было его и получить с высокой вероятностью.

Координаты текущего вектора состояния можно записать через угол \(\theta\):

\[ x = \cos{\theta} \]

\[ y = \sin{\theta} \]

На всякий случай нужно уточнить, что вспомогательный кубит не отражается на рисунке с окружностью, так как он не предназначен для обозначения индекса, а только хранит в себе его метку.

После применения функции-оракула текущий вектор отразится относительно горизонтальной оси. Объясняется это очень легко – его вертикальная компонента (вектор \(|11\rangle\)) становится отрицательной.

Вектор \(c_{1b}\) – это отражение вектора \(c\) на угол \(\theta\) вниз относительно горизонтальной оси:

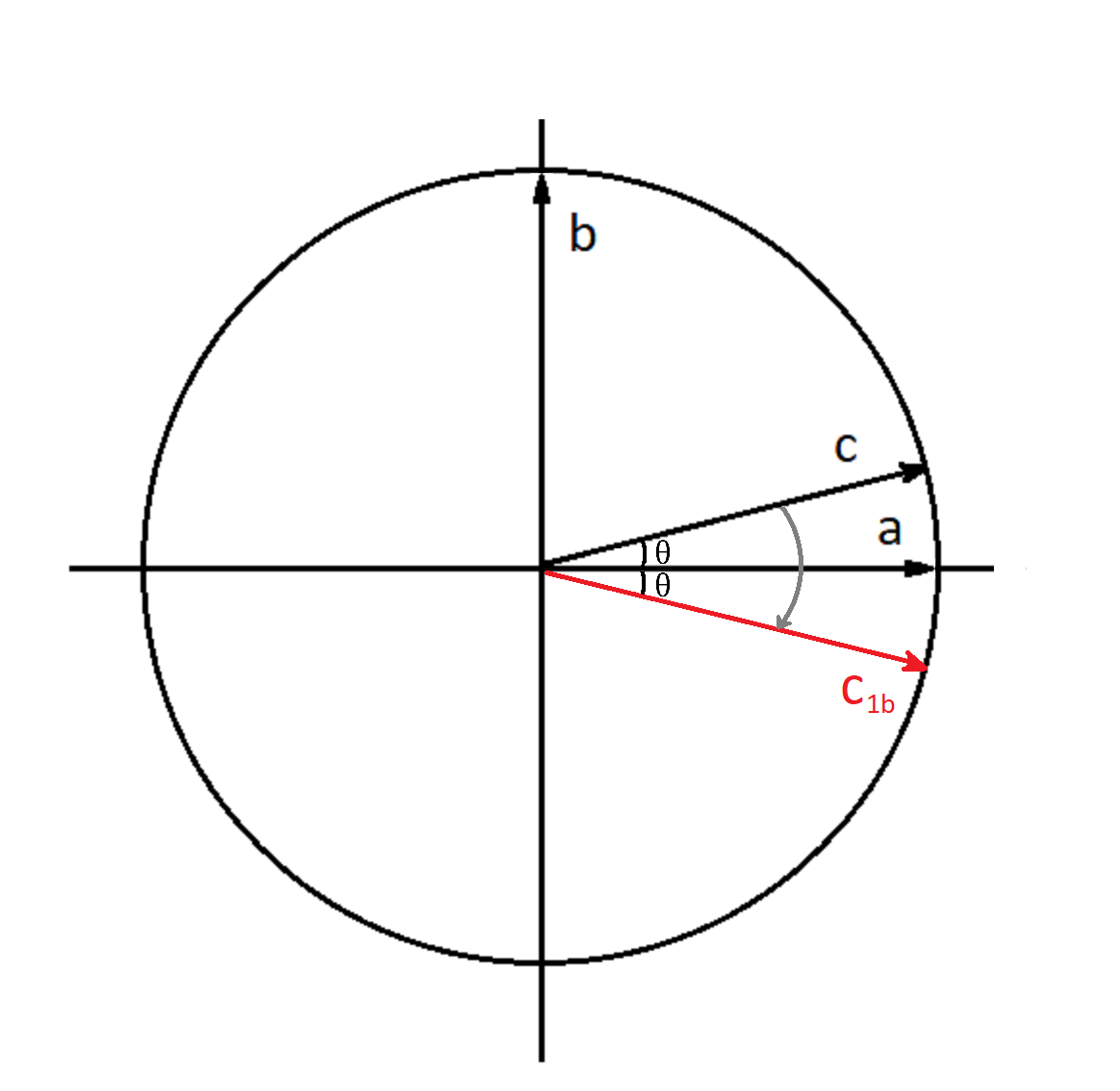
Fig. 36 Состояние системы после первой части первой итерации.

Такое отражение в нашем примере производится с помощью операции \(CCNOT\), но в общем случае операция выглядит так:

\[ U_{1b} = I - 2|b\rangle \langle b| \]

Функцию-оракул мы здесь обозначили как \(U_{1b}\). Она меняет знак только для вертикальной составляющей вектора состояния, поэтому и происходит отражение.

Проверим формулу в действии, применив ее для нашего примера:

\(U_{1b} |c\rangle = (I - 2|11\rangle \langle 11|) \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle) = \frac{1}{2} (|00\rangle + |01\rangle + |10\rangle + |11\rangle - 2|11\rangle) =\) \(= \frac{1}{2} (|00\rangle + |01\rangle + |10\rangle - |11\rangle)\)

И наконец приступаем к разбору второй части первой итерации. В ней будет происходить еще одно отражение вектора, но уже не относительно горизонтальной оси, а относительно вектора \(c\). Нетрудно заметить, что при этом текущий вектор состояния станет равен \(\cos{3 \theta}|a\rangle + \sin{3 \theta}|b\rangle\).

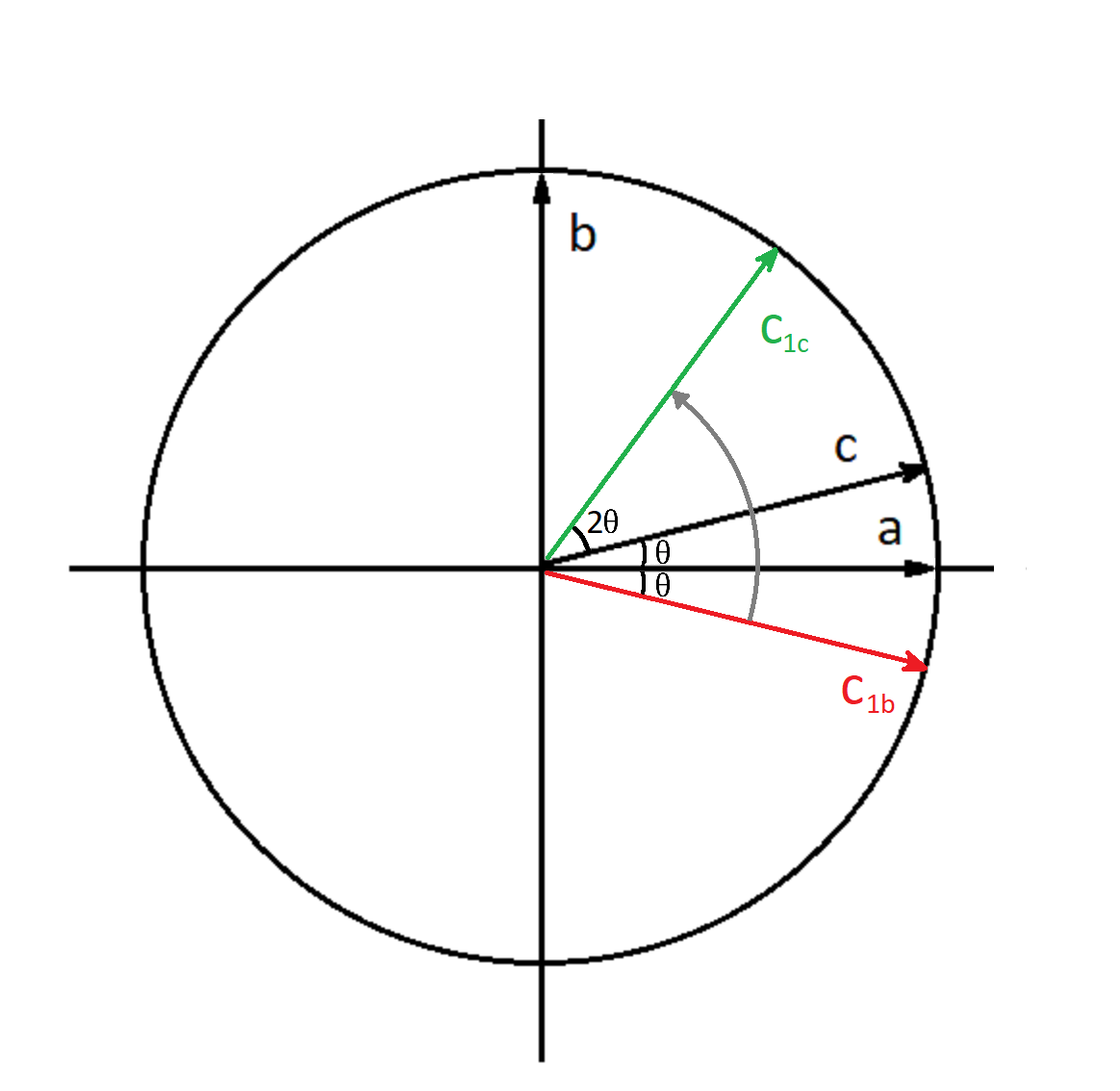
Fig. 37 Состояние системы после второй части первой итерации.

Операция для получения вектора \(c_{1c}\) будет выглядеть так:

\[ U_{1c} = 2|c\rangle \langle c| - I \]

Посчитаем, чему равен вектор \(c_{1c}\) для нашего примера:

\[U_{1c} |c_{1b}\rangle = (2|c\rangle \langle c| - I) \frac{1}{2}(|00\rangle + |01\rangle + |10\rangle - |11\rangle) = |11\rangle \]

Произошло отражение текущего вектора состояния \(|c_{1b}\rangle\) относительно вектора \(|c\rangle\). Если представить \(|c_{1b}\rangle\) как \(k_1 |c\rangle + k_2 |c_{\bot}\rangle\), где \(|c_{\bot}\rangle\) – вектор, перпендикулярный \(|c\rangle\), а \(k_1\) и \(k_2\) – действительные коэффициенты, то тогда отраженный вектор будет равен \(k_1 |c\rangle - k_2 |c_{\bot}\rangle\).

В нашей квантовой схеме эта часть итерации реализована таким образом:

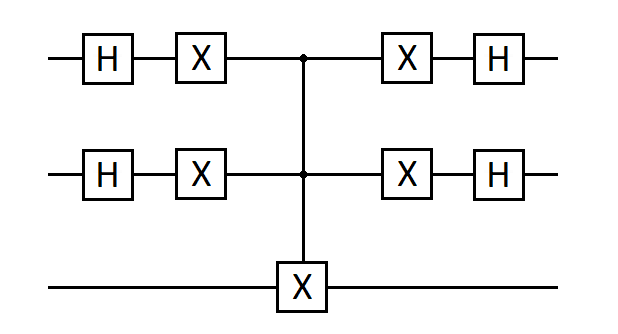
Fig. 38 Вторая часть итерации.

Вначале применяется оператор Адамара для первого и второго кубитов. Это упрощает нашу задачу, так как теперь отразить вектор состояния нужно не относительно состояния суперпозиции \(\frac{1}{2}(|00\rangle + |01\rangle + |10\rangle + |11\rangle)\), а относительно состояния \(|00\rangle\).

Далее требуется отразить вектор, то есть всем состояниям кроме нулевого присвоить минус, но мы сделаем проще: присвоим минус нулевому состоянию \(|00\rangle\), а остальные состояния, составляющие суперпозицию, оставим как есть. Сделаем это, последовательно применив гейты \(X\) и \(CCNOT\). После этого вернемся в исходную “систему координат”, применив операции в обратном порядке: сначала \(X\), а потом \(H\).

Из-за применения такого лайфхака (присвоения минуса нулевому состоянию) мы в нашем двухкубитном примере получим результат с точностью до общей фазы: не \(|11\rangle\), а \(-|11\rangle\). Но это не страшно, так как после измерения мы все равно увидим искомое значение индекса.

По рисунку, изображающему на окружности состояние системы после второй части первой итерации, видно, что в общем случае каждая последующая итерация будет приближать текущий вектор к вертикальному. Но в нашем случае угол между вектором состояния и горизонтальной осью после окончания первой итерации равен \(3 \theta\), то есть это уже и есть желаемый угол \(\frac{\pi}{2}\).

В общем случае этот угол равен \((2t + 1) \theta \approx \frac{\pi}{2}\), где \(t\) – номер произведенной итерации. Отсюда можно вывести число итераций, необходимое для работы алгоритма. При большом требуемом количестве итераций \(t\) и фиксированном \(K = 1\) (для \(K > 1\) вывод формулы аналогичный) угол \(\theta\) будет близок к \(0\), так что его можно заменить на \(\sin{\theta}\), который, в свою очередь, равен \(\frac{1}{\sqrt{N}}\):

\[ (2t + 1) \theta \rightarrow (2t + 1) \frac{1}{\sqrt{N}} \approx \frac{\pi}{2} \]

Если пренебречь единицей в скобках на основании того, что \(t\) – большое число, можно найти, что \(t\) приблизительно равно \(\frac{\pi \sqrt{N}}{4}\).

Мы уже разобрались, что каждая итерация состоит из двух частей. Первая часть – отражение вниз относительно горизонтальной оси. Вторая часть – отражение вверх относительно изначального состояния, то есть вектора \(c\). Вектор состояния всегда будет отражаться вверх на больший угол, чем в первой части итерации. Этим и будет обеспечиваться его постепенное приближение в вертикальной оси.

Мы разобрали случай, когда требуется найти один объект в таблице. Если же потребуется найти несколько объектов, то тогда, обозначив их количество за \(K\), мы должны будем проделать около \(\frac {\pi}{4} \sqrt {\frac{N}{K}}\) итераций. Таким образом, для успешной работы алгоритма Гровера необходимо знать число \(K\), чтобы можно было найти через него угол \(\theta\), а затем число итераций.

Реализация алгоритма Гровера

Итак, мы разобрали общие принципы алгоритма Гровера, а также рассмотрели конкретный пример. Настало время написать для этого примера программу.

Для начала импортируем все необходимые библиотеки и создадим схему из трех кубитов:

import pennylane as qml
from pennylane import numpy as np

dev = qml.device('default.qubit', shots=1, wires=3)

/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
  warnings.warn("Setuptools is replacing distutils.")

Начальная функция, создающая суперпозицию для каждого кубита:

def U_start():
    qml.PauliX(wires=2)
    for i in range(3):
        qml.Hadamard(wires=i)

Создадим функцию, действующую аналогично оракулу (первая часть итерации). Эта функция помечает значение индекса \(11\):

 def U_b():
    qml.Toffoli(wires=[0, 1, 2])

Вторая часть итерации:

 def U_c():
    for i in range(2):
        qml.Hadamard(wires=i)
        qml.PauliX(wires=i)

    qml.Toffoli(wires=[0, 1, 2])
    for i in range(2):
        qml.PauliX(wires=i)
        qml.Hadamard(wires=i)

Объединим первую и вторую часть итерации в одну функцию:

def U_iteration():
    U_b()
    U_c()

Переходим к итоговой функции, содержащей все шаги, а также производящей измерение кубитов в конце. В аргументе \(N\) мы должны будем указать количество итераций:

@qml.qnode(dev)
def circuit(N: int):
    U_start()
    for t in range(N):
        U_iteration()
    return qml.probs(wires=[0, 1])

Запускаем функцию и выведем ее результат:

print(circuit(N=1))

[0. 0. 0. 1.]

Так как в качестве искомого индекса выступало значение \(11\), то в результате запуска функции мы должны получить массив, состоящий из вероятностей каждого индекса, в котором искомый индекс (в нашем примере он будет последним в массиве) должен иметь наибольшую вероятность. Параметр устройства shots при необходимости можно увеличивать, не забывая о том, что его увеличение будет кратно замедлять алгоритм. Таким образом, мы нашли с помощью алгоритма Гровера искомый индекс.

Алгоритм Гровера может применяться не только для задач простого поиска в базе данных, но и как дополнительное средство ускорения для поиска экстремума целочисленной функции, а также для поиска совпадающих строк в базе данных, так что этот алгоритм, как и его модификации, сможет быть полезным в разнообразных задачах Data Science.

Задание

1. Распишите операторы \(U_{1b}\) и \(U_{1c}\) из примера в виде матриц \(4\)x\(4\) и проведите расчеты для получения \(c_{1b}\) и \(c_{1c}\) в виде векторов-столбцов.

2. Модифицируйте приведенный выше код алгоритма Гровера для двухкубитной базы данных так, чтобы искомый индекс соответствовал состоянию \(|00\rangle\).