Обзор квантовых алгоритмов
Contents
Обзор квантовых алгоритмов#
Автор(ы):
Квантовые вычисления открывают новые возможности решения задач, для которых ранее были известны только классические алгоритмы решения. С появлением идеи квантового компьютера стало понятно, что нахождение ответа для многих задач можно значительно ускорить. При этом некоторым сложным задачам, решить которые классическим способом в разумные сроки невозможно, квантовый компьютер дает реальный шанс быть решенными.
Классификация задач по временной сложности#
Вообще, в соответствии с теорией алгоритмов, задачи можно разбить на классы по временной сложности их решения. Также часто используется классификация задач по объему необходимой памяти (пространственная сложность), но нас в первую очередь волнует, насколько быстро мы сможем найти правильный ответ, так что поговорим о временной сложности. Класс задач \(P\) – это те задачи, которые возможно решить на классическом компьютере за полиномиальное время, их сложность можно представить как \(O(n^k)\). Соответственно, решение задач этого класса не является драматически затратным по времени (за исключением случаев, когда степень полинома высока, хотя такие алгоритмы и не являются типичными).
Другой класс задач – \(NP\) (расшифровывается как “недетерминировано полиномиальные”). Это класс задач, для которых неизвестно полиномиальное классическое решение. При этом проверка решения возможна за полиномиальное время. К примеру, нахождение простых множителей большого числа с помощью известных классических алгоритмов – субэкспоненциально сложная задача (работает за время, большее, чем полиномиальное, но меньшее, чем экспоненциальное). Проверить же найденное решение предельно просто: достаточно перемножить найденные простые числа.
Среди \(NP\)-задач есть наиболее сложные задачи, которые выделяют в специальную группу под названием \(NP\)-полные задачи (или \(NP\)-complete). Если найти для них быстрое решение, то этот способ решения также можно применить и к “обычным” \(NP\)-задачам.
Вообще, есть также задачи, которые, хотя и не относятся к классу \(NP\), но несмотря на это, к ним все же можно свести задачи из \(NP\)-класса. В совокупности с \(NP\)-полными задачами они образуют класс \(NP\)-трудных задач (\(NP\)-hard).
К примеру, к \(NP\)-hard задачам относится задача коммивояжера, в которой требуется установить кратчайший путь. Как решение, так и его проверка в данном случае займет суперполиномиальное время, так что эта задача не входит в класс \(NP\)-complete. Если же ее немного упростить, так что решением будет являться путь не дольше заданного, то такая разновидность задачи является примером класса \(NP\)-complete, так проверка ее решения не требует времени, большего, чем полиномиальное.
Если дать возможность классическому компьютеру решать задачи с привнесением случайности, так что компьютер получает правильный ответ с высокой вероятностью (стандартно берут порог не менее \(\frac{2}{3}\), хотя достаточно, чтобы вероятность была константой больше 0.5), то можно говорить о классе задач \(BPP\) (сокращение от англ. bounded-error, probabilistic, polynomial). Такие задачи получается решить за полиномиальное время, причем точность решения можно сколько угодно увеличивать, повторно запуская алгоритм. Квантовый аналог таких задач – класс \(BQP\) (от англ. bounded error quantum polynomial time). Это задачи, которые получается решить на квантовом компьютере за полиномиальное время, обеспечивая точность решения повторным запуском алгоритма. Наиболее известный пример такой задачи – факторизация чисел, решаемая на квантовом компьютере с помощью алгоритма Шора.
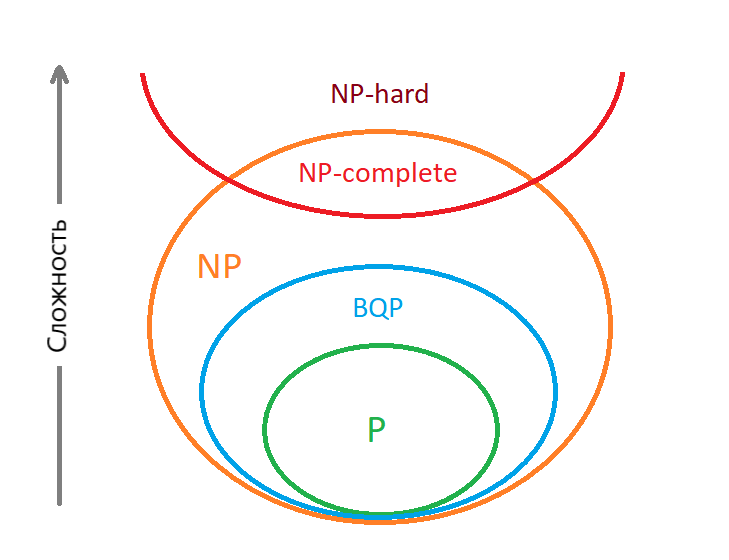
Fig. 28 Классы задач по временной сложности#
На данный момент можно говорить о том, что класс \(BQP\) включает в себя в том числе и задачи, для которых неизвестно полиномиальное классическое решение, что позволяет относиться к квантовым вычислениям с оптимизмом.
Наиболее известные квантовые алгоритмы#
Квантовые вычисления, несмотря на новые возможности, которые они предоставляют, все же не являются панацеей: не для всех классических “медленных” (то есть, не решаемых за полиномиальное время) алгоритмов пока удалось найти ускоренный квантовый аналог. Более того, многие даже более простые задачи в настоящий момент выгоднее решать на классических компьютерах. Тем не менее, уже найдены квантовые алгоритмы, работающие быстрее классических. Кратко расскажем о наиболее важных из них.
Алгоритм Шора – алгоритм, наделавший больше всего шума и привлекший внимание научно-популярных СМИ к квантовым вычислениям. Действительно, этот алгоритм дает повод для беспокойства, так как он позволяет узнавать содержание сообщений, зашифрованных с помощью алгоритма шифрования RSA. Для расшифровки требуется разложить большое число на два простых множителя. Для классического компьютера решение этой задачи может занять несколько тысяч лет, а для алгоритма Шора это дело считанных часов или даже минут. Такая скорость вычислений обусловлена тем, что на квантовом компьютере удается ускорить преобразование Фурье (как прямое так и обратное). Благодаря алгоритму Шора начала развиваться квантовая криптография – шифрование, неуязвимое для атак.
Еще один алгоритм, способный преобразить мир ИТ – алгоритм Гровера. Благодаря ему возможно ускорить поиск по базе данных. Если на классическом компьютере решить задачу поиска элемента в базе данных возможно только перебором всех элементов, то на квантовом компьютере можно получить квадратичное уменьшение сложности, так как за счет использования эффектов суперпозиции и квантовой запутанности алгоритм Гровера “просматривает” одновременно все элементы, хотя и делает это много раз, постепенно выявляя правильное решение.
Некоторые квантовые алгоритмы пока не выглядят полезными с практической точки зрения, но даже и в таком случае они уже демонстрируют возможности, которых нет в классических вычислениях. К примеру, алгоритм Дойча и алгоритм Саймона не несут особой практической пользы в силу своей простоты, но даже такие простые примеры квантовых вычислений демонстрируют значительное ускорение (в данном случае экспоненциальное). Эти алгоритмы позволяют быстро установить свойства функций. Если алгоритм Дойча определяет, является ли функция сбалансированной, то с помощью алгоритма Саймона можно вычислить период некоторой функции.
Перспективы квантовых алгоритмов#
С увеличением числа кубитов и уменьшением количества ошибок в квантовых компьютерах известные квантовые алгоритмы смогут показать себя в полной мере, но также станет возможным находить новые, более сложные и практически полезные квантовые алгоритмы. Заниматься их поиском в ближайшее время будут не только физики и математики, но и программисты, освоившие квантовые вычисления.
Алгоритмы в нашем курсе#
Для более глубокого погружения в детали этих квантовых алгоритмов у нас в курсе есть отдельные лекции по: