Алгоритм Саймона
Contents
Алгоритм Саймона#
Автор(ы):
Задача Саймона#
Давайте начнём с того, что алгоритм Саймона решает задачу Саймона. Да, вот такой замечательный учёный - нашёл проблему, решил проблему.
По своей природе задача Саймона является разновидностью задачи о скрытой абелевой подгруппе [Lom04].
Пусть задана функция \(f: \{0, 1\}^n \rightarrow \{0, 1\}^n\) и неизвестная строка \(s \in \{0, 1\}^n\), для всех \(x, y \in \{0, 1\}^n\) выполняется:
То есть, если мы для двух различных строк \(x\) и \(y\) имеем одинаковое значение \(f(x) = f(y)\), то \(x \oplus y\) равняется некоторой неизвестной строке \(s\). Функция \(f(x)\) представляет собой чёрный ящик.
Задача состоит в том, чтобы найти \(s\), выполнив при этом как можно меньшее количество вызовов \(f(x)\) .
Описание алгоритма#
Сразу определим операцию на двух бинарных строках (они же бинарные векторы) \(x = x_0 x_1 x_2 ... x_{2^n-1}\), \(z = z_1 z_2 z_3 ... z_{2^n-1}\):
Принципиальная схема алгоритма Саймона:
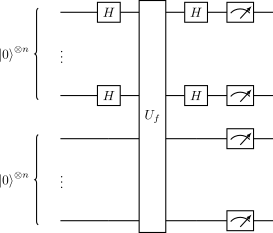
В принципе, есть небольшие вариации в реализации алгоритма, мы рассмотрим наиболее простую (все необходимые ссылки в конце приведены):
Сначала приготовления. Вначале мы приготовим 2 набора квантовых регистров (каждый размерности \(n\)) в следующем состоянии:
\[ |\psi_0\rangle = |0\rangle|0\rangle \]Применяем гейты Адамара на первом регистре:
\[ (H^n \otimes I^n) |\psi_0\rangle = (H^n \otimes I^n) |0\rangle |0\rangle = |\psi_1 \rangle = \frac{1}{\sqrt{2^n}}\sum_{x \in \{ 0, 1\}^n}|x\rangle |0\rangle \]Применяем оператор \(U_f\), который выполняет следующее преобразование \(U_f(|x\rangle|0\rangle) = |x\rangle|f(x)\rangle\), т.е. во второй регистр записывается значение функции \(f(x)\):
\[ U_f(|\psi_1 \rangle) = U_f(\frac{1}{\sqrt{2^n}}\sum_{x \in \{ 0, 1\}^n}|x\rangle |0\rangle) = |\psi_2\rangle = \frac{1}{\sqrt{2^n}}\sum_{x \in \{ 0, 1\}^n}|x\rangle |f(x) \rangle \]Производим измерение на втором регистре. Измеренное значение будет соответствовать либо \(x\) либо \(y = x \oplus s\) . А первый регистр примет значение:
\[ |\psi \rangle_3 = \frac{1}{\sqrt{2}} \left( |x\rangle_1 + |y\rangle_1 \right) \]Снова применяем гейты Адамара на первом регистре:
\[ (H^n \otimes I^n) |\psi_2\rangle = |\psi_3\rangle = \frac{1}{2^n} \sum_{z \in \{ 0, 1\}^n}(-1^{\langle x, z\rangle} + -1^{\langle y, z\rangle}) |z\rangle, \](операцию \(\langle x, z \rangle\) мы уже определяли выше).
Note
Для чисел \(x = 110111\) и \(z = 010101\) получим
\[ \langle x, z\rangle = 1 \wedge 0 \oplus 1 \wedge 1 \oplus 0 \wedge 0 \oplus 1 \wedge 1 \oplus 1 \wedge 0 \oplus 1 \wedge 1 = 1 \]\[ (-1)^{1} = -1 \]Производим измерение на первом регистре. И здесь возможны 2 варианта исхода:
\( x \oplus y = s = 0^n \)
Учитывая \( x \oplus y = 0^n \) и то, что состояние всей системы описывается как
\[ \sum_{z \in \{0, 1\}^n}|z\rangle \otimes \frac{1}{2^n} \sum_{x \in \{0, 1\}^n}(-1^{\langle x, z\rangle}) |f(x) \rangle \]находим вероятность получить строку \(z\) на первом регистре
\[ p_z = \left\| \frac{1}{2^n} \sum_{z \in \{0, 1\}^n} \left((-1)^{\langle z, x\rangle} |f(x)\rangle \right) \right\|^2 = \frac{1}{2^n} \]т.е. в данном случае имеет место равномерное распределение.
\( x \oplus y = s \neq 0^n \)
Этот случай гораздо интереснее. Функция \(f\) преобразует два различных входных значения \(x_1, x_2 \in \{0,1\}^n\) в одно \(f(x_1) = f(x_2) = s \in \{0, 1\}^n\) . Также \(x_1 \oplus x_2 = s\) эквивалентно \(x_1 \oplus s = x_2\).
\[ |\psi_3\rangle = \frac{1}{2^n}\sum_{z \in \{0, 1 \}^n}\sum_{x \in \{0, 1 \}^n} \frac{(-1)^{\langle z, x \rangle} (1 + (-1)^{\langle z, s\rangle})}{2} |z\rangle \oplus |f(x)\rangle= \]\[ \frac{1}{2^n}\sum_{z \in \{0, 1 \}^n}|z\rangle \otimes \sum_{x \in \{0, 1 \}^n} \frac{(-1)^{\langle z, x\rangle} (1 + (-1)^{\langle z, s\rangle})}{2} |f(x)\rangle \]\[ p_z = \left\| \frac{1}{2^n} \sum_{x \in \{0, 1\}^n} \left((-1)^{\langle x, z\rangle} |f(x)\rangle \right) \right\|^2 = \left\| \frac{1}{2^n} \sum_{z \in A} \left(((-1)^{\langle x_1, z\rangle} + (-1)^{\langle x_2, z\rangle})|z\rangle \right) \right\|^2 \]\[\begin{split} = \begin{cases} \frac{1}{2^{n-1}}, \text{ если } \langle z, s \rangle = 0 \\ 0, \text{ если } \langle z, s \rangle = 1 \end{cases} \end{split}\]
Расчёты вероятностей можно найти в приложениях Приложение 1.
Выполняем алгоритм \(n\) раз. После чего у нас будет система \(n\) линейно независимых уравнений. Теперь приступаем к вычислению строки \(s\).
Постобработка.
Итак, для того, чтобы найти \(s = (s_0, s_1, s_2, ..., s_{n-1})^T\), нам потребуется \(n\) линейно независимых векторов \(\vec{z_i}\), для которых выполняется \(\langle \vec{z_i}, s \rangle = 0\).
После того как получена система из \(n\) линейно независимых уравнений, решение можно найти методом Гаусса.
Пример#
Давайте возьмём n = 3, строку \(s = 100\), и функцию \(f\), которая соответствует критерию
Обычно функция \(f(x)\) задана наперёд. Ну а мы выберем её простейшей: \(f(x) = x \oplus s\).
Давайте посмотрим на таблицу истинности всех нужных переменных.
Нарисуем схему на Qiskit, которая будет показывать одну итерацию алгоритма:
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister
# Работаем в пространстве размерности n = 3
n = 3
# Создаём необходимые регистры
qr1 = QuantumRegister(n, name="q1")
qr2 = QuantumRegister(n, name="q2")
cr1 = ClassicalRegister(n, name="c1")
# Шаг 1. Создаём квантовую схему (инициализация состояния)
qc = QuantumCircuit(qr1, qr2, cr1)
# Шаг 2. Применяем гейт Адамара ко всем кубитам первого регистра
qc.h(range(n))
# Шаг 3. Применяем U_f
qc.cx(qr1[0], qr2[0])
# Шаг 4. Производим измерение второго регистра
qc.measure(qr2, cr1)
# Шаг 5. Ещё раз применяем гейт адамара к каждому из кубитов
qc.h(range(n))
# Шаг 6. Производим измерение первого регистра
qc.measure(qr1, cr1)
# Рисуем схему
qc.draw()
┌───┐ ┌───┐ ┌─┐
q1_0: ┤ H ├──■──┤ H ├──────┤M├
├───┤ │ ├───┤┌─┐ └╥┘
q1_1: ┤ H ├──┼──┤ H ├┤M├────╫─
├───┤ │ ├───┤└╥┘┌─┐ ║
q1_2: ┤ H ├──┼──┤ H ├─╫─┤M├─╫─
└───┘┌─┴─┐└┬─┬┘ ║ └╥┘ ║
q2_0: ─────┤ X ├─┤M├──╫──╫──╫─
┌─┐ └───┘ └╥┘ ║ ║ ║
q2_1: ─┤M├────────╫───╫──╫──╫─
└╥┘ ┌─┐ ║ ║ ║ ║
q2_2: ──╫───┤M├───╫───╫──╫──╫─
║ └╥┘ ║ ║ ║ ║
c1: 3/══╩════╩════╩═══╩══╩══╩═
1 2 0 1 2 0 При использовании Pennylane схема выглядит следующим образом:
import pennylane as qml
import matplotlib.pyplot as plt
from typing import Tuple, List
n = 3
dev = qml.device("default.qubit", shots=128, wires=n*2)
def simon_start(N: int) -> None:
for i in range(N):
qml.Hadamard(wires=i)
def simon_oracle(N: int) -> None:
qml.CNOT(wires=[0, N])
def simon_after_oracle(N: int) -> None:
for i in range(N):
qml.Hadamard(wires=i)
@qml.qnode(dev)
def simon_circuit(N: int) -> Tuple[List[List[int]], List[List[int]]]:
simon_start(N)
simon_oracle(N)
simon_after_oracle(N)
wx = range(0, N)
wfx = range(N, N*2)
return qml.sample(wires=wx), qml.sample(wires=wfx)
# Схема возвращает массив результатов измерений первого
# регистра: x, и массив результатов измерения 2-го регистра: f(x).
# количестов измерений (samples) задано через shots
x, fx = simon_circuit(N=n)
fig, ax = qml.draw_mpl(simon_circuit)(N=n)
fig.show()
/home/runner/work/qmlcourse/qmlcourse/.venv/lib/python3.8/site-packages/_distutils_hack/__init__.py:33: UserWarning: Setuptools is replacing distutils.
warnings.warn("Setuptools is replacing distutils.")
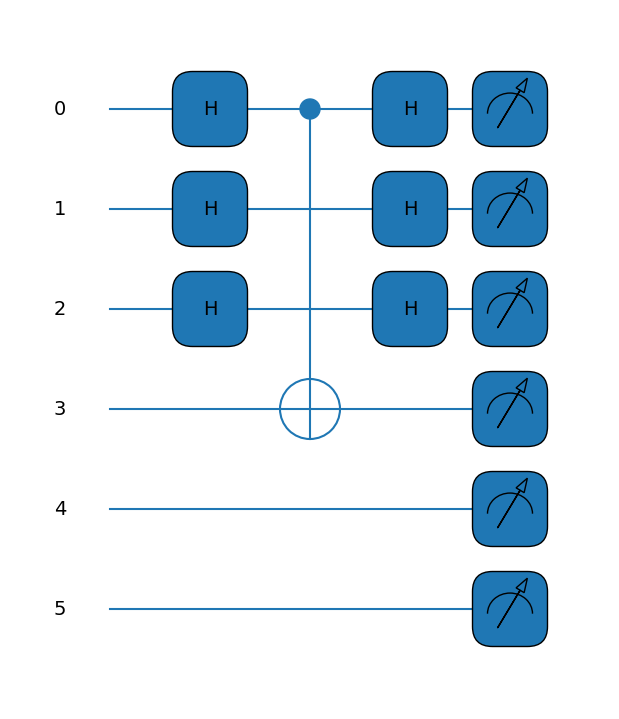
Note
Созданная с помощью Pennylane схема визуально отличается от полученной с помощью Qiskit, так как Pennylane не позволяет выполнять операции с кубитами после выполнения измерения. Но так как с кубитами Y ([3, 4, 5]) после операции измерения не должно выполняться никаких действий, результат получается тот же самый.
Теперь пройдём по всем шагам алгоритма:
Инициализация всех регистров в \(0\) состоянии:
\[ |\psi_0\rangle = |000\rangle_{1} |000\rangle_{2} \]Применяем Адамар к первому регистру:
\[\begin{split} (H^n \otimes I)(|\psi_0\rangle) = |\psi_1\rangle = \frac{1}{\sqrt{8}}(|000\rangle + |001\rangle + |010\rangle + |011\rangle \\ + |100\rangle + |101\rangle + |110\rangle + |111\rangle)_1 |000 \rangle_{2}) \end{split}\]Применяем оракул \(U_f\):
\[ \begin{align}\begin{aligned}\begin{split} U_f(|\psi_1\rangle = |\psi_2\rangle = \\\end{split}\\\begin{split} \frac{1}{\sqrt{8}} (|000\rangle_{1} |0 \oplus 0, 0, 0 \rangle_{2} \\ + |001\rangle_{1} |0 \oplus 0, 0, 0 \rangle_{2} \\ + |010\rangle_{1} |0 \oplus 0, 0, 0 \rangle_{2} \\ + |011\rangle_{1} |0 \oplus 0, 0, 0 \rangle_{2} \\ + |100\rangle_{1} |0 \oplus 1, 0, 0 \rangle_{2} \\ + |101\rangle_{1} |0 \oplus 1, 0, 0 \rangle_{2} \\ + |110\rangle_{1} |0 \oplus 1, 0, 0 \rangle_{2} \\ + |111\rangle_{1} |0 \oplus 1, 0, 0 \rangle_{2} ) \end{split}\end{aligned}\end{align} \]Измеряем второй регистр. С вероятностью \(\frac{1}{2}\) мы получим либо значение \(|000\rangle\) либо \(|100\rangle\). Допустим результат равен \(|100\rangle\). Тогда состояние первого регистра примет вид: \(|\psi_3\rangle = (|100\rangle_{1} + |101\rangle_{1} + |110\rangle_{1} + |111\rangle_{1})\).
Ещё один раз применяем гейты Адамара на первый регистр:
\[ |\psi_4 \rangle = \frac{1}{4} [ \left(|0\rangle - |1\rangle) \otimes (|0\rangle + |1\rangle) \otimes (|0\rangle + |1\rangle) \right) \]\[ + \left(|0\rangle - |1\rangle) \otimes (|0\rangle + |1\rangle) \otimes (|0\rangle - |1\rangle) \right) \]\[ + \left(|0\rangle - |1\rangle) \otimes (|0\rangle - |1\rangle) \otimes (|0\rangle + |1\rangle) \right) \]\[ + \left(|0\rangle - |1\rangle) \otimes (|0\rangle - |1\rangle) \otimes (|0\rangle - |1\rangle) \right) ] \]Производим измерение первого регистра, записывая результат.
Выполняем шаги 1-6 \(n\) раз.
Здесь решаем систему уравнений.
Приложение#
Расчёт вероятностей.
Случай, когда \(x \oplus z = 0^n\) :
\[ \sum_{z \in \{0,1\}^n} |z\rangle \otimes \left( \frac{1}{2^n} \sum_{x \in \{0,1\}^n} ((-1)^{\langle x, z \rangle} |f(x)\rangle) \right) \]Вероятность получить какую-либо из \(2^n\) строк одинакова:
\[ p_z = \left\| \frac{1}{2^n} \sum_{z \in \{0, 1\}^n} \left((-1)^{\langle z, x\rangle} |f(x)\rangle \right) \right\|^2 = \frac{1}{2^n} \]Утверждение, данное выше, следует из того, что \(f(x)\) отличается от \(x\) лишь порядком во всём множестве строк \(\{0,1\}^n\):
\[ \left\| \frac{1}{2^n} \sum_{z \in \{0, 1\}^n} \left((-1)^{\langle z, x\rangle} |f(x)\rangle \right) \right\|^2 = \left\| \frac{1}{2^n} \sum_{z \in \{0, 1\}^n} \left((-1)^{\langle z, x\rangle} |x\rangle \right) \right\|^2 \]Случай, когда \(x \oplus z = s \neq 0^n\):
Определим \(A = f(\{0,1\}^n)\) - образ функции \(f\), \(f(x_i) = \ell \in A\) - т.е. это какое-то значение функции \(f\). Здесь у нас имеются два таких значения \(x_1 \in \{0, 1\}^n \), \(x_2 \in \{0, 1\}^n \) , что для них выполняется \( x_2 = s \oplus x_1 \).
\[ p_z = \left\| \frac{1}{2^n} \sum_{\ell \in A} \left( ((-1)^{\langle z, x_1\rangle} + (-1)^{\langle z, x_2\rangle}) |\ell\rangle \right) \right\|^2 = \frac{1}{2^n} \]Перепишем коэффициенты \((-1)^{\langle x_1, z \rangle} + (-1)^{\langle x_2, z \rangle}\):
\[ (-1)^{\langle x_1, z \rangle} + (-1)^{\langle x_2, z \rangle} = (-1)^{\langle x_1, z \rangle} + (-1)^{\langle x_2 \oplus s, z \rangle} \]Также, заметим, что выполняется \(\langle x_1 \oplus s, z \rangle = \langle x_1, z \rangle \oplus \langle x_2, z \rangle\), тогда ещё раз перепишем:
\[ (-1)^{\langle x_1, z \rangle} (1 + (-1)^{\langle z, s \rangle}) \]И собирая все полученные условия:
\[ p_z = \left\| \frac{1}{2^n} \sum_{\ell \in A} \left( (-1)^{\langle x_1, z \rangle} (1 + (-1)^{\langle z, s \rangle}) |\ell\rangle \right) \right\|^2 = \frac{1}{2^n} \]Если \(\langle z, s \rangle = 1\), то \((-1)^{\langle z, s \rangle} = -1\) и следовательно
\[ (-1)^{\langle x_1, z \rangle} (1 + (-1)^{\langle z, s \rangle}) = (-1)^{\langle x_1, z \rangle} (1 - 1) = 0 \]И вероятность в таком случае равняется 0
\[ p_z = \left\| \frac{1}{2^n} \sum_{\ell \in A} \left( (-1)^{\langle x_1, z \rangle} (1 + (-1)^{\langle z, s \rangle}) |\ell\rangle \right) \right\|^2 = 0 \]Иначе \(\langle z, s \rangle = 0\), и тогда \((-1)^{\langle z, s \rangle} = 1\):
\[ (-1)^{\langle x_1, z \rangle} (1 + (-1)^{\langle z, s \rangle}) = 2 (-1)^{\langle x_1, z \rangle} \]Вычисление вероятности
\[ p_z = \left\| \frac{1}{2^n} \sum_{\ell \in A} (-1)^{\langle x_1, z \rangle} 2 |\ell\rangle \right\|^2 = \]\[ \left\| \frac{2}{2^n} \sum_{\ell \in A} (-1)^{\langle x_1, z \rangle} |\ell\rangle \right\|^2 = \left\| \frac{2}{2^n} \sum_{\ell \in A} (-1)^{\langle x_1, z \rangle} |\ell\rangle \right\|^2 = \left\| \frac{1}{2^{n-1}} \sum_{\ell \in A} (-1)^{\langle x_1, z \rangle} |\ell\rangle \right\|^2 \]\[\begin{split} p_z = \begin{cases} \frac{1}{2^{n-1}}, \text{ если } \langle z, s \rangle = 0 \\ 0, \text{ если } \langle z, s \rangle = 1 \end{cases} \end{split}\]
