О квантовом машинном обучении
Contents
О квантовом машинном обучении#
Автор(ы):
Квантовое машинное обучение – это на самом деле огромная область, и наш курс охватывает лишь небольшую ее часть. В этой обзорной лекции мы попробуем взглянуть на картину в целом и посмотреть, какие есть направления в этой интересной и динамично развивающейся области.
Note
Эта статья является исключительно обзорной – в ней будет много красивых картинок, но мы не будем вдаваться в формулы, которые могут эти картинки объяснить. Цель лекции – познакомить читателя с тем, как машинное обучение может быть применено в разных задачах, связанных с квантовыми вычислениями и квантовой физикой.
Виды квантового машинного обучения#
Как мы помним из лекции по машинному обучению, в таких задачах у нас есть две важных составляющих – данные и алгоритм. В случае квантового машинного обучения у нас появляется некоторая “вариативность”:
квантовые данные
квантовый алгоритм
классические данные
классический алгоритм
На базе этого можно построить классификацию машинного обучения.
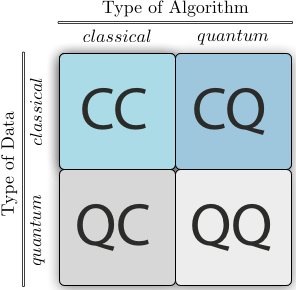
Fig. 56 Виды машинного обучения в зависимости от типа данных и алгоритма.#
Когда мы имеем классические данные и классический алгоритм, то это как раз обычное машинное обучение, рассмотренное во вводной лекции курса. А вот остальные виды мы рассмотрим далее.
Квантовые данные и классический алгоритм#
Классическое машинное обучение применительно к квантовым данным – это очень активно развивающаяся область квантовой физики и квантовой химии. Главный вопрос в данном случае – что именно мы пониманием под “квантовыми данными”. Но мы будем придерживаться максимально широкой трактовки этого понятия. Далее рассмотрим примеры возможного применения ML в задачах квантовой физики и химии.
NQS#
Neural Quantum States это очень перспективное улучшение квантового Монте-Карло – популярного метода приближенного решения задач квантовой физики. Мы будем подробно рассматривать проблему нахождения энергетических спектров квантомеханических систем, а также моделирования квантовой динамики в блоке о проблемах квантового машинного обучения. Пока нам достаточно знания того, что эти задачи являются вычислительно трудными и их прямое численное решение очень быстро становится невозможным по мере увеличения размера системы и числа взаимодействующих частиц. В подходе NQS, впервые опубликованном в журнале Science [CT17], предложено моделировать волновую функцию \(\ket{\Psi}\) физической системы при помощи глубокой нейронной сети. Это дает ряд преимуществ над обычным квантовым Монте-Карло в плане точности моделирования, а также позволяет явно симулировать time-dependent уравнение Шредингера. Относительно другого популярного метода, который называется Matrix Product State NQS дает лучшую масштабируемость и меньшую аппроксимацию сложность, которая оказывается линейной по числу частиц в физической системе.
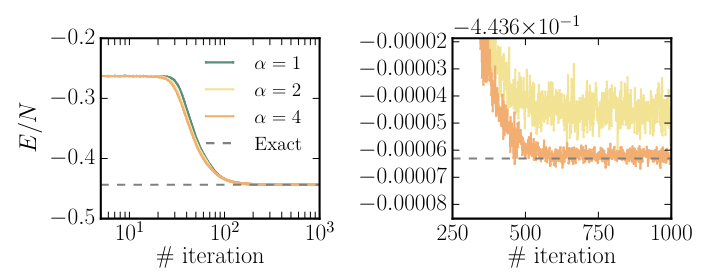
Fig. 57 Сходимость NQS по энергии в зависимости от числа эпох обучения. По вертикали значение энергии на один спин, по горизонтали эпохи обучения. Пунктиром отмечено точное значение, полученное прямой диагонализацией гамильтониана. Слева общий вид, справа – сверхтонкая сходимость вблизи энергии основного состояния. Источник [CT17].#
CNN над потенциалами#
Другим интересным подходом является применение Convolutional Neural Networks (CNN) – специального класса глубоких нейронных сетей, разработанных для обработки изображений, к физическим потенциалам. Дело в том, что трехмерный энергетический потенциал можно представить как 2D изображение. Например, можно взять периодическую потенциальную энергию, создаваемую атомами в кристаллической решетке и рассмотреть, как будет вести себя электрон в таком потенциале.
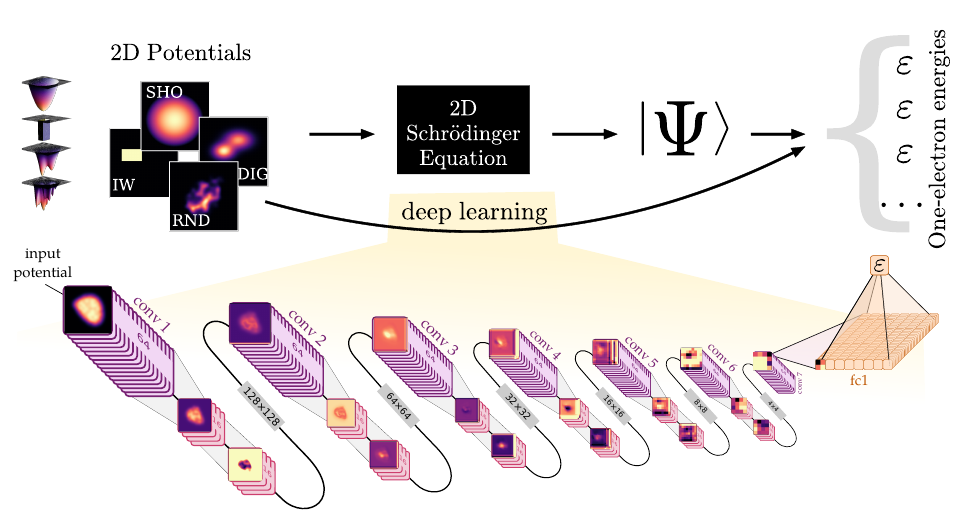
Fig. 58 Иллюстрация применения CNN на энергетических потенциалах. Источник [MST17].#
Существует ограниченный набор частных случаев, когда эта задача может быть решена аналитически. Используя такие точные решения, мы составляем обучающую выборку, тренируем CNN, а потом можем применять ее к другим, более сложным потенциалам.
Решение уравнения Шредингера#
Другим примером решения задачи об энергетических уровнях является применение глубокой нейронной сети, которая на вход принимает Slater determinants, Jastrow factor и другие известные способы приближенного описания квантомеханических систем. А на выходе из такой глубокой нейронной сети получаем волновую функцию системы. Таким образом, получается объединить все преимущества хорошо изученных физических представлений с высокой экспрессивностью глубоких нейронных сетей [HSchatzleNoe20].
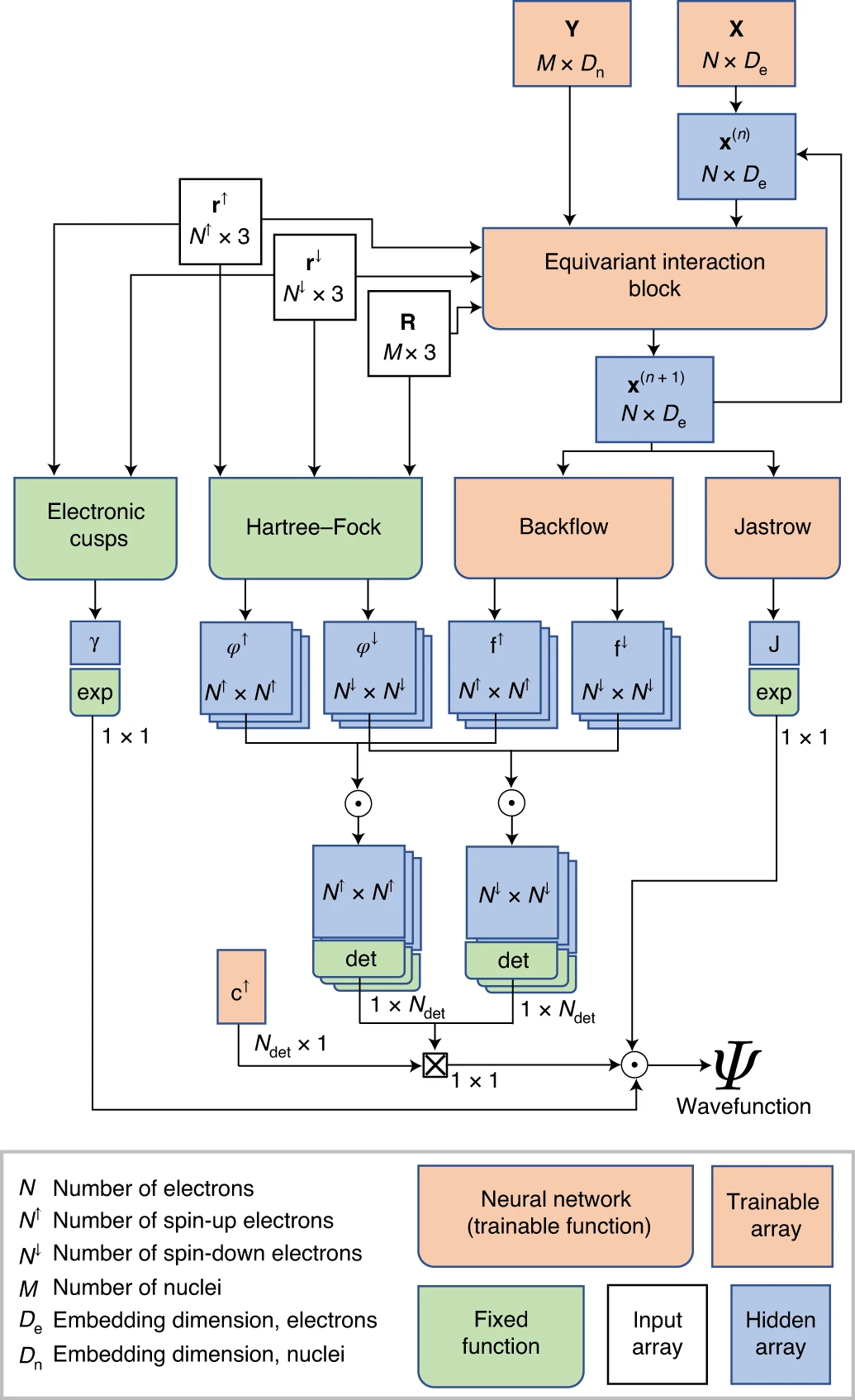
Fig. 59 Архитектура подхода PauliNet. Источник [HSchatzleNoe20].#
Такой подход дает фантастическую точность по сравнению с другими подходами и выглядит очень перспективно, так как дополнительно позволяет получить очень хорошую масштабируемость из-за возможности снизить число slater determinants.
RNN для моделирования волновых функций#
Другой похожий на NQS подход – это использовать для аппроксимации волновой функции рекуррентные нейронные сети вместо машин Больцмана.
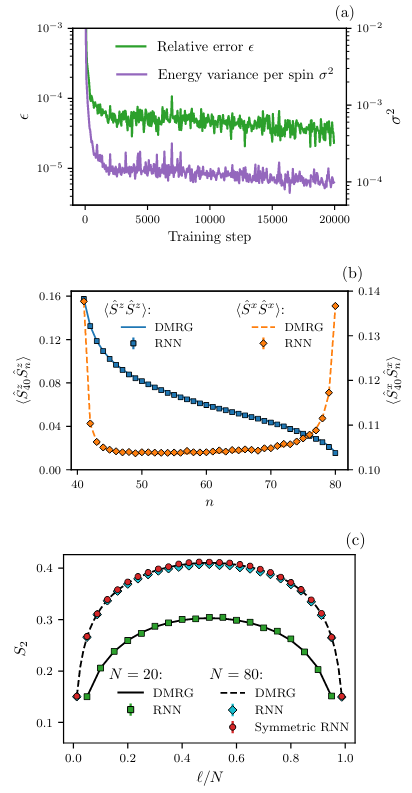
Fig. 60 Результаты RNN-модели для аппроксимации волновых функций. Можно получать не только значение энергии, но и ожидаемые значения других операторов, например, операторов спина или операторов спиновых корреляций. Источник [HAGH+20]. На графике (a) приведена зависимость энергии от эпохи обучения. На графике (b) приведены зависимости собственного значения операторов спиновых корреляций 40-го (центрального) спина с n-ым от номера n. На графике (c) приведено распределение значений оператора спина по длине цепочки спинов.#
В данном подходе мы строим “последовательную” волновую функцию многочастичной квантовой системы, “подавая” туда по одной каждую частицу. А так как нейронная сеть – рекуррентная, мы по сути последовательно строим волновую функцию многочастичной системы.
Квантовая томография#
Мы немного рассказывали о задаче квантовой томографии в лекции про смешанные состояния. Правда, там привели пример использования метода максимизации правдоподобия для решения задачи восстановления состояния по измерениям. Оказывается, что для этих целей можно использовать глубокие нейронные сети. Один из таких подходов описан в [AMunozNK21]. Суть подхода в том, что используются генеративные сети с условием – Conditional GAN (C-GAN) для восстановления состояния. Для создания матрицы плотности используется генератор, а для вычисления ошибки относительно реальных результатов измерений – дискриминатор.
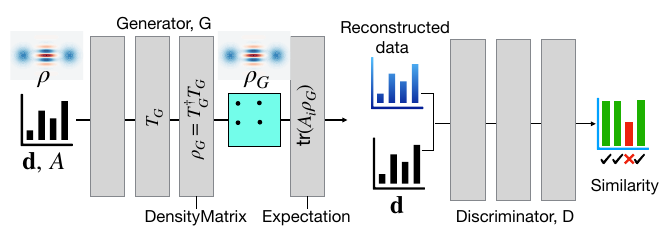
Fig. 61 Иллюстрация подхода C-GAN.#
Заключение к подразделу#
В целом, применение классических алгоритмов машинного обучения к задачам квантовой физики и квантовой химии – очень перспективная область. Мы еще немного коснемся этой темы, когда будем рассматривать решение задачи о собственных значениях гамильтонианов. Однако, эта тема выходит за рамки нашего курса.
Классические данные и квантовый алгоритм#
Теперь перейдем к ситуации, когда мы рассматриваем классические данные (задачи классификации и регрессии) и применяем к ним машинное обучение, реализуемое на квантовом компьютере как набор операций над кубитами.
HHL#
Один из самых известных алгоритмов квантового машинного обучения – это алгоритм HHL [HHL09], которому в нашем курсе посвящена отдельная продвинутая лекция. Это алгоритм решения системы линейных уравнений за \(O(N \log N)\) операций. Так как к решению системы уравнений можно свести огромное число задач реального мира, этот алгоритм обладает огромным потенциалом. К сожалению, сегодня его практическое применение сильно ограничено несколькими вещами:
необходимость эффективной генерации начального состояния – без этого достижения превосходства HHL невозможно;
высокие требования к точности операций, а также необходимость в большом числе кубитов.
Этот алгоритм является примером чисто квантового алгоритма, где абсолютно все операции выполняются на квантовом компьютере.
Quantum k-NN#
Другой пример полностью квантового алгоритма – это модификация классического алгоритма ближайшего соседа, с той лишь разницей, что для вычисления расстояний между точками в \(N\)-мерном пространстве мы используем квантовый компьютер. Этот алгоритм называется Quantum k-NN (Quantum k Nearest Neighbours). Сегодня существует довольно много потенциально эффективных реализаций этого алгоритма, которые отличаются в основном тем, какая используется метрика расстояния в гильбертовом пространстве. Одна из реализаций рассмотрена в продвинутой лекции нашего курса. К сожалению, практическое использование таких алгоритмов сегодня ограничено тем, что для них требуется эффективная квантовая память – quantum Random Access Memory.
Заключение к подразделу#
Сегодня мы живем в так называемой NISQ (Noisy Intermediate-Scale Quantum) эпохе, то есть когда у нас есть квантовые компьютеры лишь ограниченного размера и с относительно большим уровнем шумов. А чисто квантовые алгоритмы квантового машинного обучения очень требовательны именно к точности вычислений. Также в таких алгоритмах большой проблемой является постоянная необходимость сложной операции перевода классических данных в квантовые. В теории, эта проблема исчезнет с появлением qRAM, однако сегодня такая “квантовая память” еще не существует и даже пока нет однозначного понимания того, как именно ее делать. Все это сильно ограничивает потенциал полностью квантовых подходов. Далее мы рассмотрим более перспективный в NISQ-эпоху подход – гибридное квантово-классическое машинное обучение.
Гибридное обучение#
Большая часть из оставшихся лекций нашего курса будет посвящена как раз гибридным методам квантового машинного обучения. В этих методах часть алгоритма реализуется в виде квантовых вентилей, а часть выполняется на классическом компьютере.
VQC#
Variational Quantum Circuits, или просто вариационные схемы, – это одно из центральных понятий в гибридном квантово-классическом обучении. Основная идея заключается в том, что мы используем квантовую операцию, которая задается каким-то классическим параметром. Обычно это одна или несколько операций “вращений” на сфере Блоха, про которые мы говорили в лекции про квантовые гейты. При этом вариация классического параметра осуществляется на классическом компьютере, например, при помощи градиентного спуска.
Fig. 62 Схема работы вариционной квантовой схемы.#
В нашем курсе теме вариационных схем будет посвящено несколько лекций:
Также мы часто будем возвращаться понятию VQC в теме квантовых нейросетей, а также в блоке про решение задачи собственных значений при помощи алгоритма Variational Quantum Eigensolver.
Квантовые нейросети#
Квантовые “нейронные сети” – это как раз пример, когда мы комбинируем вариационные слои вместе с обычными слоями нейронных сетей.
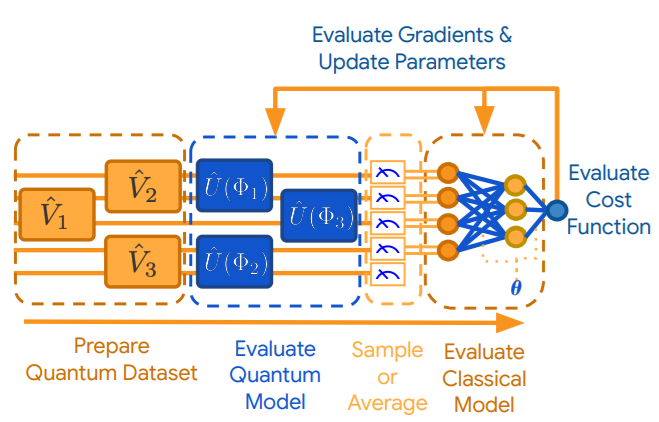
Fig. 63 Пример гибридной квантовой нейросети. Источник [BVM+21].#
На картинке выше приведен пример комбинации вариационных квантовых схем и классических слоев обычных глубоких нейронных сетей. При этом оптимизация параметров выполняется при помощи единого процесса backpropagation, с той лишь разницей, что для классических и квантовых слоев немного по-разному вычисляется градиент для параметров конкретного слоя. Теме квантовых нейронных сетей в нашем курсе будет посвящен целый блок, где будет, в том числе, рассказано еще и об аналоге сверточного слоя с использованием VQC.
Квантовые ядра#
Квантовые ядра и квантовый алгоритм Support Vector Machine (SVM) – это другой пример, как можно объединить квантовые гейты с классическими алгоритмами. Математике “под капотом” классического SVM у нас будет посвящена отдельная лекция, но если кратко, то суть там в том, что решение задачи об оптимальной разделяющей гиперплоскости (другими словами, об оптимальной классификации) можно выразить через скалярные произведения точек обучающей выборки. Причем не обязательно в исходном пространстве, а в любом гильбертовом пространстве. А как мы помним, квантовые гейты как раз представляют собой операции в гильбертовом пространстве, причем экспоненциально большого размера. Так и появляется идея гибридного SVM – мы переписываем скалярные произведения точек как результат измерения параметризованных квантовых схем, где параметры это и есть компоненты каждой из точек. А дальше уже применяем классические методы решения оптимизационной задачи. Этой теме у нас будет посвящена отдельная лекция.
Оптимизация энергии#
Еще один интересный и перспективный класс задач, которые можно решать гибридными методами – это оптимизация энергии гамильтониана. Может показаться, что это еще что-то из области квантовой физики, но на самом деле в блоке о проблемах квантового машинного обучения мы покажем, как к задаче поиска основного состояния системы, описанной квантовым оператором – гамильтонианом, можно свести огромное число задач реального мира. Например, это задача Коммивояжера, очень важная в области логистики, или задача о нахождении энергий электронов, которая играет важную роль в разработке лекарств или создании новых материалов.
Заключение#
В этой лекции мы познакомились с тем, каким может быть квантовое машинное обучение. Мы узнали, что бывают:
классические алгоритмы над квантовыми данными;
квантовые алгоритмы над классическими данными;
гибридные алгоритмы.
Именно гибридные алгоритмы наиболее перспективны в NISQ-эпоху, и именно им будет посвящена большая часть оставшихся лекций курса.