Квантовые нейронные сети
Contents
Квантовые нейронные сети#
Автор(ы):
Описание лекции#
В этой лекции мы пройдёмся по расширению идеи нейронных сетей на квантовые компьютеры – мы уже прошли и вариационные квантовые схемы (VQC), и комбинацию квантовых и классических градиентов в них в соответствующих блоках. Всё что осталось – это объединить всё изученное в общую картину и заняться обучением этих самых квантовых нейронных сетей. Для того чтобы лучше разобраться в том, какие ограничения и возможности предоставляет этот подход, мы приведём несколько публикаций о квантовых и гибридных генеративных состязательных сетях.
Введение#
Как уже было упомянуто в лекции по VQC, на данный момент квантовые вычислители ещё недостаточно развиты для того, чтобы в одиночку решать большие задачи, имеющие практическое значение для индустрии – это в особенной степени актуально для нейронных сетей, которые и в классическом сценарии требуют значительных вычислительных ресурсов. Именно поэтому на данный момент наиболее популярна категория гибридных вариационных алгоритмов, которые обучают квантовую параметрическую схему (QNN) при помощи классической оптимизации, например, VQ Eigensolvers и Quantum Approximate Optimization Algorithms. В общем и целом идея гибридных алгоритмов заключается в оптимизации над некоторым классом параметрических вычислений для минимизации энергии волновой функции (VQE/QAOA), экстракции нелокальной информации (QNN Classifiers) или генерации данных, соответствующих квантовому распределению (Quantum Generative Models).
Применение#
Лучше всего понять адекватность и применимость какой-то технологии, особенно основанной на комплексном научном базисе, позволяет как раз таки ее применение - чего удалось добиться кому-то на практике и насколько результаты пригодны для того, чтобы хвататься за технологию. Вместе с тем, практические результаты дадут нам глубже понять и в последствии объяснить, как гибридные сети работают под капотом. Приведём два примера, которые хорошо показывают разницу в ограничениях при использовании полностью квантовых и гибридных квантово-классических сетей.
В первом примере была построена полностью квантовая генеративная состязательная сеть, задачей которой являлось воспроизвести MNIST, однако у всего эксперимента был один нюанс. Из-за текущего размера квантовых вычислителей было предложено уменьшить размерность MNIST с 784 до 4 при помощи метода главных компонент (PCA), чтобы его хоть как-то можно было отправить в квантовую схему. Очевидно, сеть такого размера не в состоянии тягаться с классическими сетями на десятки тысяч весов, поэтому конечным результатом стало сравнение по количеству весов при идентичных результатах. Полностью квантовая сеть смогла получить такие же результаты, как и классическая, при это имея на 95% меньше параметров. Эти результаты всё ещё поднимают вопрос того, будут ли они справедливыми для моделей, адекватно справляющихся с задачей.
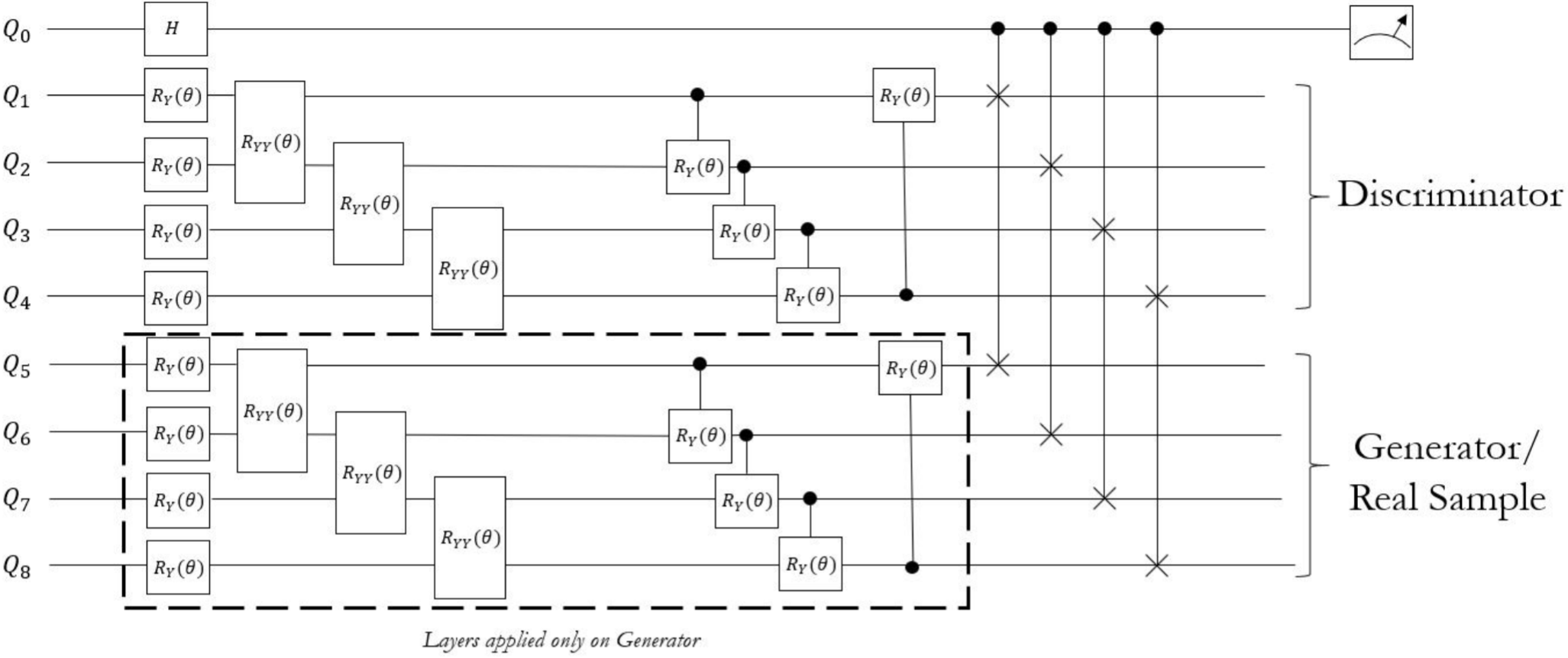
Fig. 77 Схема квантовой генеративной состязательной сети из публикации [SBC+21].#
Во втором примере была построена гибридная квантово-классическая генеративная состязательная сеть, задачей которой являлось воспроизвести QM-9 – популярный датасет молекул до 9 атомов, представленный молекулярным графом в виде матрицы 9 на 9 и атомарным вектором из 9 элементов. Генеративная часть модели состояла из нескольких квантовых схем и, по большей части, классической сети, предсказывающей узлы и связи между ними. Дискриминативная часть была полностью классической во всех вариациях модели. В конечном итоге им удалось добиться снижения числа параметров по сравнению с полностью классической сетью на 85% и, при увеличении числа кубитов, на 98%. Таким образом они показали, что комбинация классических и квантовых схем должна соответствовать той же самой закономерности, что и полностью квантовые сети.
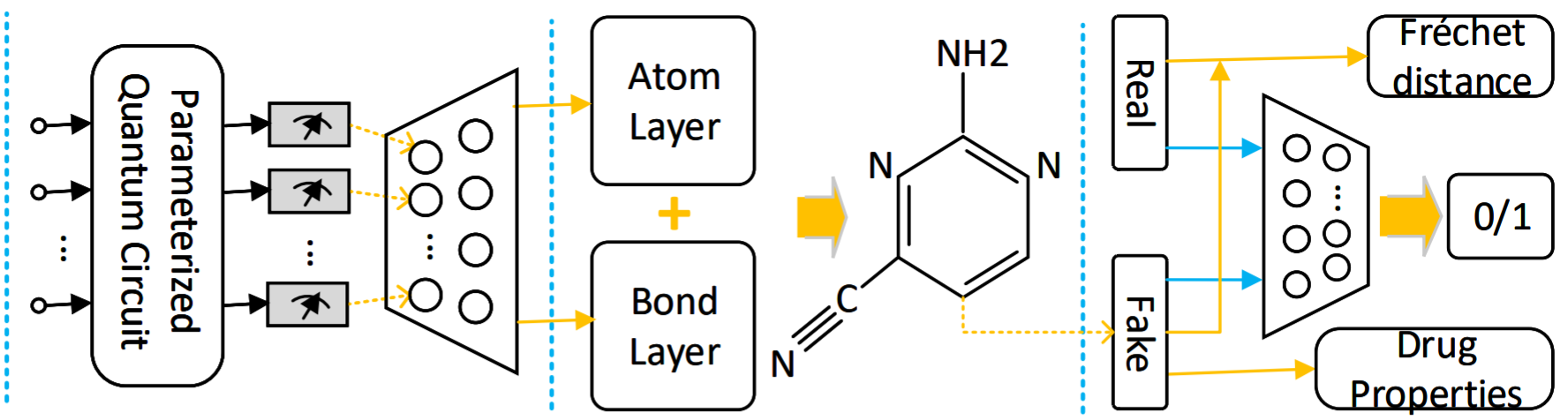
Fig. 78 Схема гибридной генеративной состязательной сети из публикации [LTG21].#
За счёт большей актуальности на текущих практических задачах именно последнего, гибридного подхода, дальнейшая часть лекции будет рассматривать именно его.
Архитектура#
В идеале этот подход подразумевал бы, что при помощи классического оптимизатора мы обучаем некоторую параметрическую схему на квантовом вычислителе, однако в текущих реалиях NISQ этот подход невозможен, поэтому большая часть параметрической схемы остаётся на классических вычислителях. В данном блоке мы поговорим о подходе, связанном с QNN Classifiers, которые следуют вышеупомянутому принципу и обучаются градиентным спуском практически так же, как и обычные классические сети, позволяя градиенту протекать между квантовой и классической частью сети.
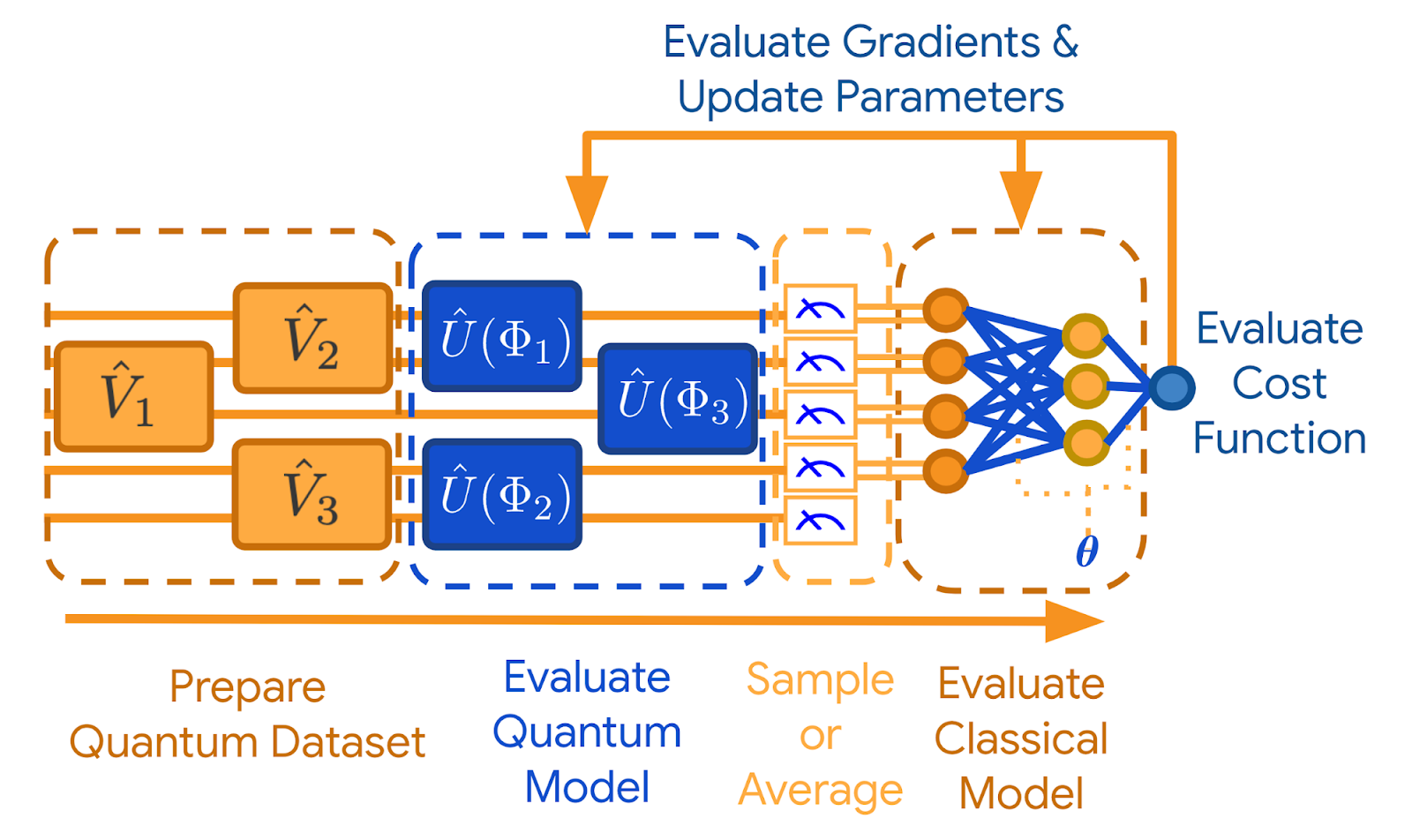
Fig. 79 Схема обучения гибридной нейронной сети из [BVM+21].#
На изображении гибридной сети процедура практически идентична классическому обучению сетей, в котором добавляется процесс кодирования классических данных в квантовые операторы и процесс измерения квантового состояния для того, чтобы передать уже классическую информацию для дальнейших вычислений на классическом устройстве, как это было описано в лекции по VQC.
Анзац#
Зачастую в литературе по VQC, особенно когда речь идёт о нейронных сетях, упоминается такая вещь как ansatz – по своей сути это заранее подготовленные участки параметрической схемы, которые могут быть использованы как составные блоки сети. Если проводить параллели с классическим машинным обучением, то в рамках библиотеки PennyLane эти схемы называются templates (шаблоны) и могут представлять собой, например, свёрточный слой или эмбеддинг, а также более общие элементы квантовой схемы вроде подготовки состояний или перестановок между кубитами. Более подробно мы остановимся на них слегка позже в курсе, в одной из следующих глав, а пока что в общих чертах пройдёмся по обучению квантовых нейронных сетей без сложностей внутренней кухни.
Note
Интересно, но термин anzatz пришел в квантовые вычисления и QML из теоретической физики. Этот термин имеет немецкое происхождение, так как в первой половине XX века именно немецкие научные журналы были самыми передовыми. Частое употребление этого термина в отношении квантового машинного обучения объясняется тем, что большая часть специалистов в этой области это именно люди, занимающиеся теоретической физикой.
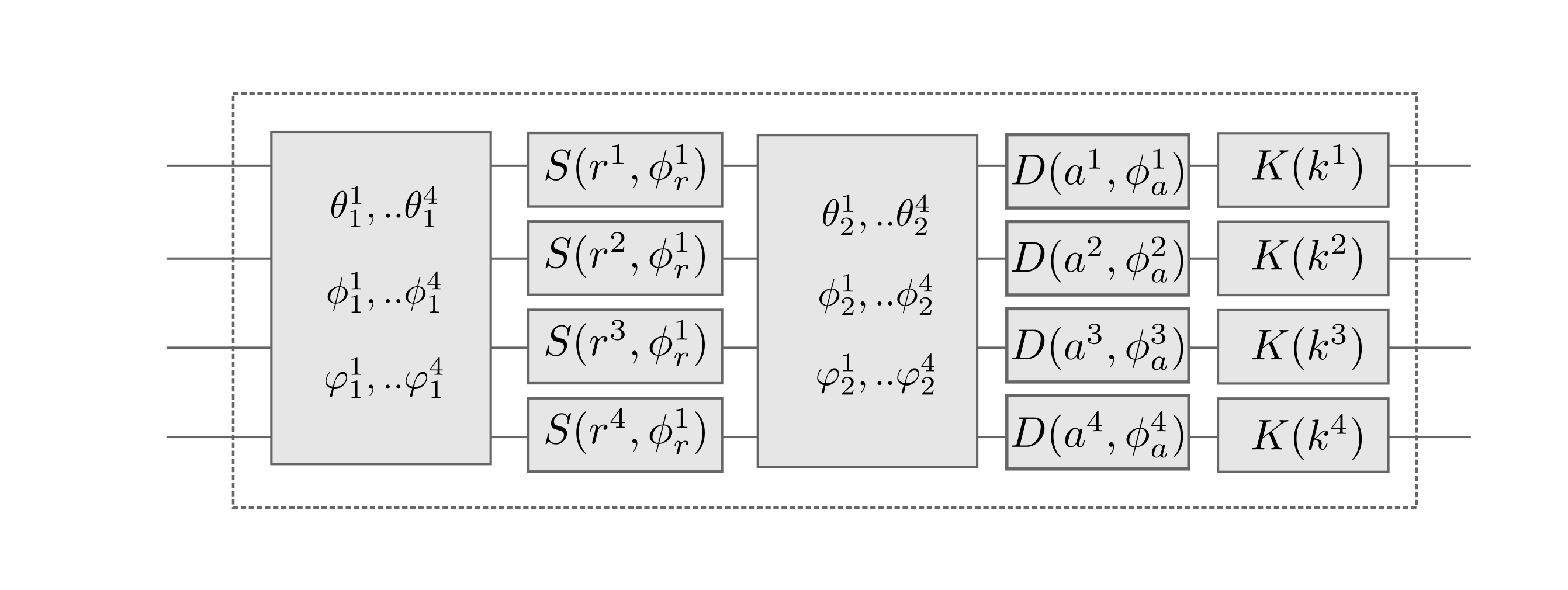
Fig. 80 Ansatz, соответствующий свёрточному слою нейронной сети в PennyLane. Источник#
Функция потерь#
Функция потерь работает таким же образом, как и в полностью классических сетях, так как оптимизация происходит на классическом железе. Единственное, что отличается, – это объединение квантовых и классических градиентов. Градиент по нашей квантовой схеме получается при помощи замера состояния, которое может варьироваться из-за вероятностной природы кубита, поэтому несколько замеров позволяют аппроксимировать ожидаемый градиент при помощи методов вроде finite differences или parameter-shift, после чего остаётся только совместить его с классическим градиентом.
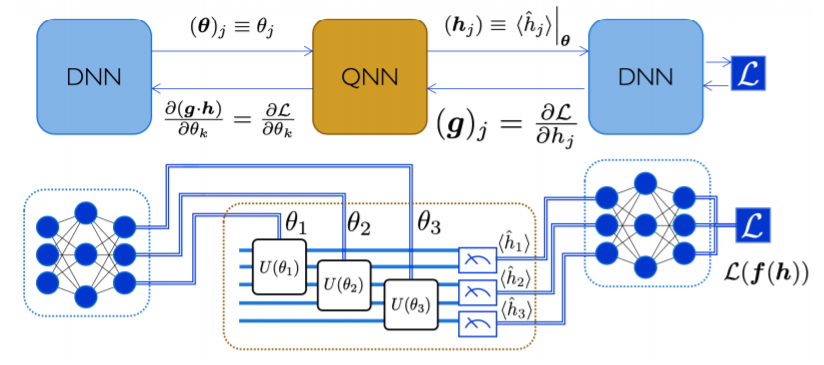
Fig. 81 Распространение градиентов от функции потерь в гибридной схеме.#
Сеть от начала до конца#
В конечном итоге мы имеем следующую последовательность действий для того, чтобы собрать гибридную нейронную сеть:
трансформировать данные из классических в квантовые представления;
отправить эти данные для вычисления на квантовой схеме;
просэмплировать и замерить результат квантовой схемы;
отправить результаты для вычисления на классической схеме;
оценить ошибку, рассчитать градиенты и обновить параметры.
Что мы узнали из лекции#
В ближайшие годы полностью квантовые нейронные сети не смогут решать задачи целиком, поэтому будут использоваться в качестве составляющей гибридного квантово-классического решения.
Так же как и для полностью квантовых сетей, гибридные сети позволяют уменьшить количество необходимых параметров по сравнению с полностью классическими сетями.
Обучение подобных сетей практически идентично обучению классических сетей за исключением нескольких трюков, необходимых для работы с параметрами квантовых схем.
